一、题目
若函数
在
( A )
( B )
( C )
( D )
二、解析
这道题可以根据函数连续的定义解出。
函数
因此,若函数
观察题目可知,这是一个分段函数,且当
当
根据如下的等价无穷小原则:
于是有:
原式
为了满足上面提到的函数在一点处连续的定义,需要有:
化简形式得:
由此可知,选
EOF
若函数
在
( A )
( B )
( C )
( D )
这道题可以根据函数连续的定义解出。
函数
因此,若函数
观察题目可知,这是一个分段函数,且当
当
根据如下的等价无穷小原则:
于是有:
原式
为了满足上面提到的函数在一点处连续的定义,需要有:
化简形式得:
由此可知,选
EOF
判断函数
在 MATLAB (下面的代码在 MATLAB 9.1.0.441655 (R2016b) 中测试通过) 中输入如下代码:
x=0:0.01:10; semilogy(x,log(x))
可以绘制出
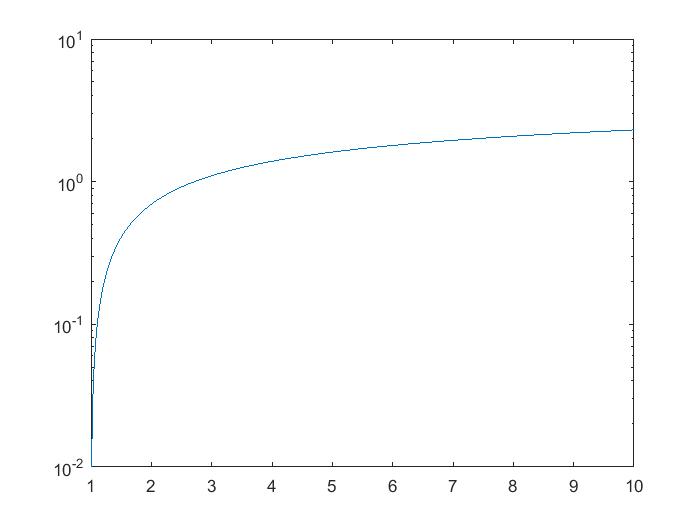
有图像可以看到,自然对数
因为:
则:
当
到这里,定义域的问题解决了,下面要解决的是函数是关于
由于:
则:
上面的运算结果符合奇函数的定义,因此,
此外,使用 WolframAlpha 画出的函数
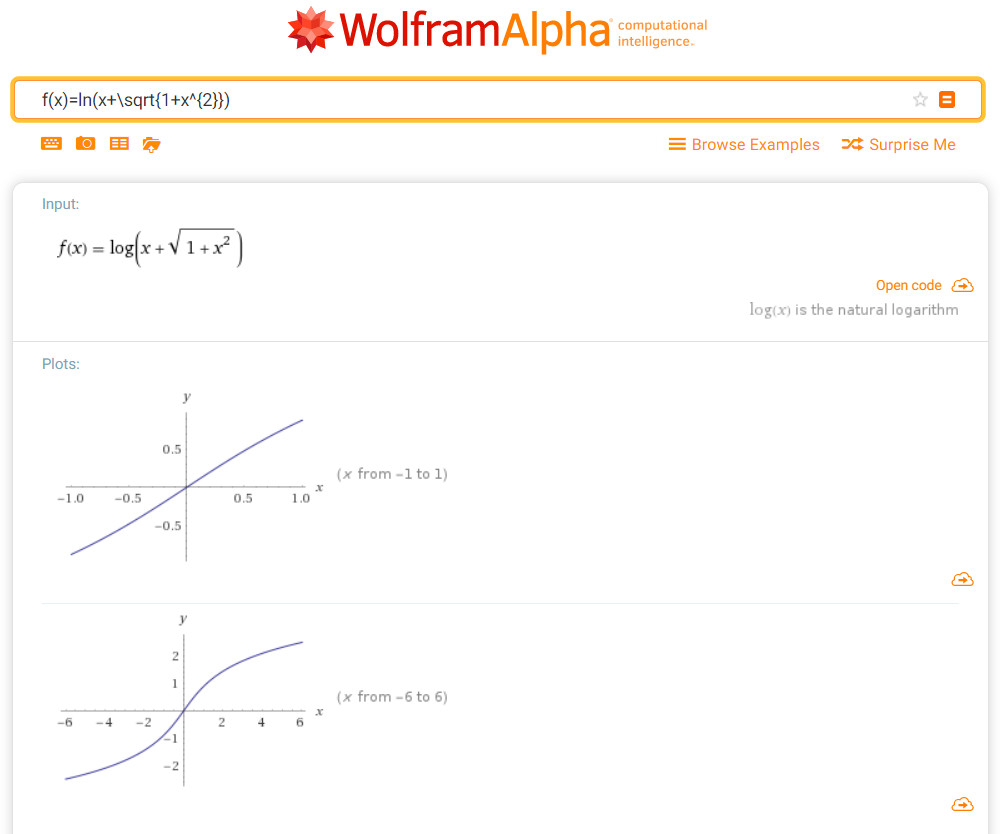
由图像我们也可以看出这是一个奇函数。
EOF
使用四则运算将原式化简,之后使用等价无穷小替换求出结果。
由于当
根据等价无穷小的如下替换原则:
(详细内容可以参考荒原之梦网(zhaokaifeng.com)的这篇文章:高等数学中常用的等价无穷小)
可知:
观察题目中的式子可以发现,当
(1)
(2)
(3)
附近两者都可导(在
综上可知,此处可以使用
求导过程如下:
原式
因为,当
上面的计算过程依次是“求导 / 化简 / 化简 / 化简 / 化简”。下面开始正式使用
经过上面的求导,我们发现,当
原式
在使用洛必达法则解决该问题的时候,进行了两次求导。其实,只要满足以下三个条件,则在使用洛必达法则的过程中可以进行任意次求导,但需要注意的是,每一次求导之前必须确保式子仍然满足如下三个条件,否则不能使用洛必达法则:
设:
(01)
(02)
(03)
总结来说,洛必达法则的使用方法如下:
观察题目中的式子我们发现,可以使用麦克劳林展开式的
代入公式可得:
于是有:
原式
EOF
上面这个计算过程是错的,错误的原因是在计算
很显然,一个二维函数中不可能有两个不同的自变量,而且根据约定可知,当式子中出现
这里我们可以使用复合函数求导的链式法则计算本例题,复合函数的链式求导法则如下:
设
于是,对于例题的正确求导过程如下:
当
(01) 当
Tips:
- 在上面的等价无穷小公式中,表示常数的符号
也可以是一个极限为常数的式子。
例如这个极限公式中的 既可以是一个常数,也可以是一个极限为常数的式子——也就是说,表示 的这个式子的极限必须存在。 - 当
不是趋于零而是趋于某个常数的时候也可以借助上面的等价无穷小公式解题,可以参考《只有当 x 趋于零的时候才能用等价无穷小代换吗?不,x 趋于 1 的时候也可以试试看》。
依次点击下方按钮,深入学习高等数学中的常用等价无穷小: