分类： 考研数学

八、解答题 (本题满分 10 分)

设抛物线 $y=a x^{2}+b x+C$ 过原点, 当 $0 \leqslant x \leqslant 1$ 时 $y \geqslant 0$, 又已知该抛物线与 $x$ 轴及直线 $x=1$ 所围图形的面积为 $\frac{1}{3}$. 试确定 $a, b, c$ 的值, 使此图形绕 $x$ 轴旋转一周而成的旋转体的体积 $V$ 最小.

首先：

$$
x=0, y=0 \Rightarrow y=a x^{2}+b x+c \Rightarrow c=0 \Rightarrow
$$

接着，求面积：

$$
S=\int_{0}^{1}\left(a x^{2}+b x\right) \mathrm{~d} x=\frac{1}{3} \Rightarrow
$$

$$
\left.\left(\frac{1}{3} a x^{3}+\frac{1}{2} b x^{2}\right)\right|_{0} ^{1}=\frac{1}{3} a+\frac{1}{2} b=\frac{1}{3}
$$

求体积：

$$
V=\pi \int_{0}^{1}\left(a x^{2}+b x\right)^{2} \mathrm{~d} x=
$$

$$
\pi \int_{0}^{1}\left(a^{2} x^{4}+b^{2} x^{2}+2 a b x^{3}\right) \mathrm{~d} x \Rightarrow
$$

$$
V=\left.\pi\left(\frac{1}{5} a^{2} x^{5}+\frac{1}{3} b^{2} x^{3}+\frac{1}{4} \cdot 2 a b x^{4}\right)\right|_{0} ^{1} \Rightarrow
$$

$$
V=\pi\left(\frac{a^{2}}{5}+\frac{b^{2}}{3}+\frac{a b}{2}\right) \Rightarrow
$$

又：

$$
b=\frac{2}{3}(1-a)
$$

因此：

$$
V=\pi\left[\frac{a^{2}}{5}+\frac{\frac{4}{9}(1-a)^{2}}{3}+\frac{\frac{2}{3} a(1-a)}{2}\right]
$$

$$
V=\pi\left[\frac{a^{2}}{5}+\frac{4}{27}(1-a)^{2}+\frac{1}{3} a(1-a)\right] \Rightarrow
$$

$$
V_{a}^{\prime}=\pi\left[\frac{2}{5} a+\frac{4}{27} \cdot 2(1-a) \cdot(-1)+\frac{1}{3}(1-2 a)\right] \Rightarrow
$$

$$
V_{a}^{\prime}=\pi\left(\frac{2}{5} a-\frac{8}{27}+\frac{8 a}{27}+\frac{1}{3}-\frac{2 a}{3}\right) \Rightarrow
$$

$$
V_{a}^{\prime}=\pi\left(\frac{4}{135} a+\frac{1}{27}\right) \Rightarrow V_{a}^{\prime}=0 \Rightarrow
$$

$$
a=\frac{-1}{27} \cdot \frac{135}{4}=\frac{-5}{4} \Rightarrow b=\frac{3}{2}
$$

又：

$$
V_{a}^{\prime \prime}=\frac{4 \pi}{135}>0
$$

因此，当 $\begin{cases}
& a = \frac{-5}{4} \\
& b = \frac{3}{2} \\
& c = 0
\end{cases}$ 时，体积最小。

---

八、解答题 (本题满分 8 分)

设 $f(x)$ 在 $(-\infty,+\infty)$ 上有连续导数, 且 $m \leqslant f(x) \leqslant M$.

(1) 求 $\lim \limits_{a \rightarrow 0^{+}} \frac{1}{4 a^{2}} \int_{-a}^{a}[f(t+a)-f(t-a)] \mathrm{d} t$

积分中值定理，存在 $\xi \in[-a, a]$, 使得：

$$
\int_{-a}^{a}[f(t+a)-f(t-a)] \mathrm{~ d} t=
$$

$$
[a-(-a)][f(\xi+a)-f(\xi-a)]=
$$

$$
2 a[f(\xi+a)-f(\xi-a)]
$$

又由拉格朗日中值定理, 存在 $c \in(\xi-a, \xi+a)$, 使得：

$$
\frac{f(\xi+a)-f(\xi-a)}{(\xi+a)-(\xi-a)}=f^{\prime}(c) \Rightarrow
$$

$$
f(\xi+a)-f(\xi-a)=2 a f^{\prime}(c) \Rightarrow
$$

$$
\int_{-a}^{a}[f(t+a)-f(t-a)] \mathrm{~ d} t=4 a^{2} f^{\prime}(c) \Rightarrow
$$

$$
\lim \limits_{a \rightarrow 0^{+}} \frac{1}{4 a^{2}} \int_{-a}^{a}[f(t+a)-f(t-a)] \mathrm{~ d} t=
$$

$$
\lim \limits_{a \rightarrow 0^{+}} f^{\prime}(c)=\lim \limits_{c \rightarrow 0} f^{\prime}(c)=f^{\prime}(0)
$$

(2) 证明 $\left|\frac{1}{2 a} \int_{-a}^{a} f(t) \mathrm{d} t-f(x)\right| \leqslant M-m(a>0)$.

$$
m \leqslant f(x) \leqslant M \Rightarrow
$$

$$
2 a m \leqslant \int_{-a}^{a} f(x) \mathrm{~ d} x \leqslant 2 a M \Rightarrow
$$

$$
m \leqslant \frac{1}{2 a} \int_{-a}^{a} f(x) \mathrm{~ d} x \leqslant m \tag{1}
$$

又：

$$
-M \leqslant-f(x) \leqslant-m \tag{2}
$$

联立 $(1)$, $(2)$ 可得：

$$
-(M-m) \leqslant \frac{1}{2 a} \int_{-a}^{a} f(x) \mathrm{~ d} x-f(x) \leqslant M-m
$$

$$
\left|\frac{1}{2 \alpha} \int_{-a}^{a} f(x) \mathrm{~ d} x-f(x)\right| \leqslant M-m \quad(a>0)
$$

---

十、解答题 (本题满分 10 分)

在第一象限内求曲线 $y=-x^{2}+1$ 上的一点, 使该点处的切线与所给曲线及两坐标轴所围 成的图形面积为最小, 并求此最小面积.

根据题目，我们可以绘制出如图 02 所示的示意图：

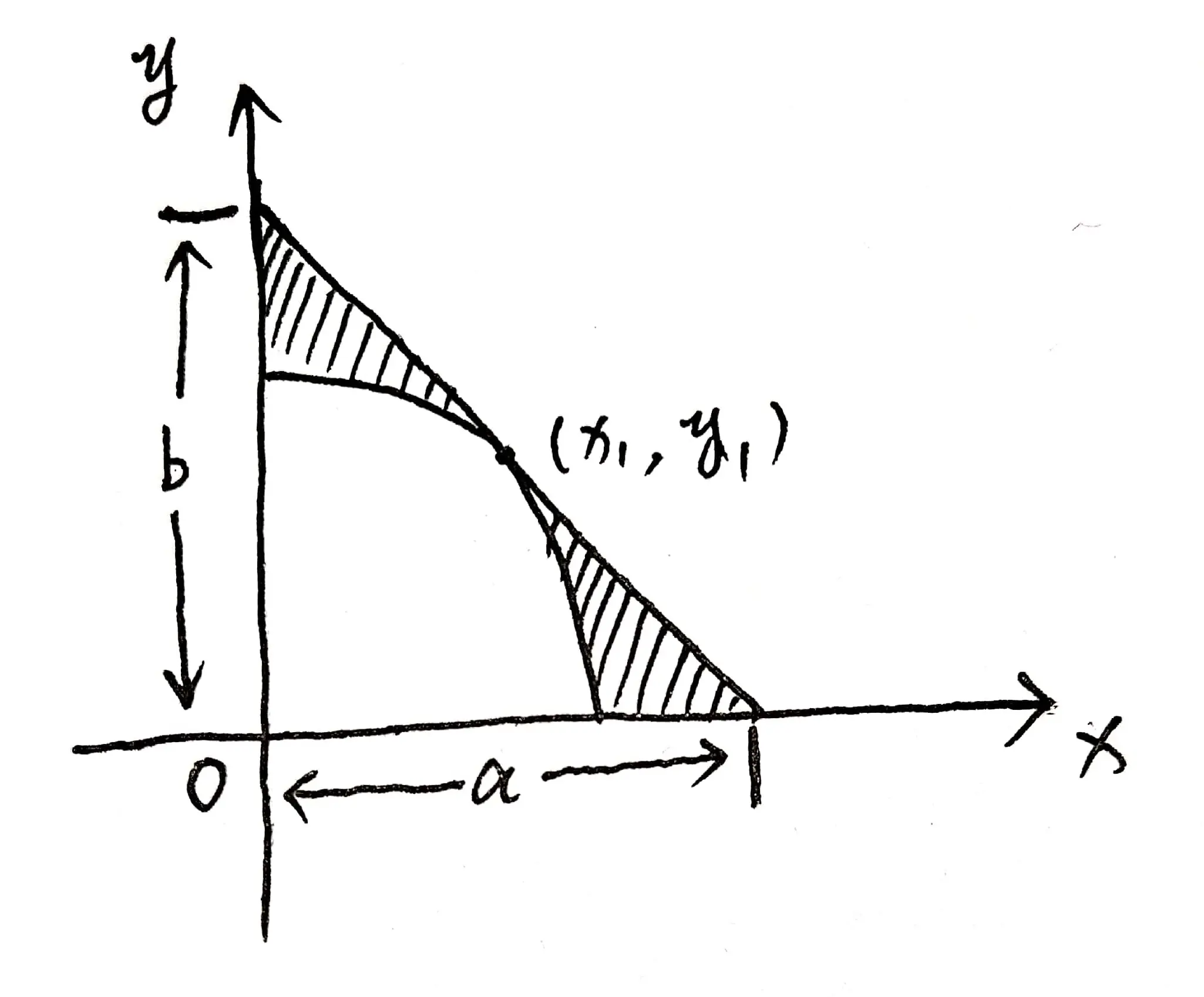
设切点为 $\left(x_{1}, y_{1}\right)$, 则：

$$
y=-x^{2}+1 \Rightarrow y^{\prime}=-2 x \Rightarrow
$$

即斜率为：

$$
k=-2 x_{1}
$$

对应的切线为：

$$
y-y_{1}=-2 x_{1}\left(x-x_{1}\right)
$$

在 $x$ 轴上的截距为：

$$
x=0 \Rightarrow b=y=2 x_{1}^{2}+y_{1}=2 x_{1}^{2}+\left(-x_{1}^{2}+1\right) \Rightarrow
$$

$$
b=x_{1}^{2}+1
$$

在 $y$ 轴上的截距为：

$$
y=0 \Rightarrow-y_{1}=-2 x_{1}\left(a-x_{1}\right) \Rightarrow
$$

$$
-y_{1}=-2 a x_{1}+2 x_{1}^{2} \Rightarrow x_{1}^{2}-1=-2 a x_{1}+2 x_{1}^{2}
$$

$$
2 a x_{1}=x_{1}^{2}+1 \Rightarrow
$$

$$
a=\frac{x_{1}^{2}+1}{2 x_{1}}
$$

于是，要求解的三角形的面积表达式为：

$$
S=\frac{1}{2} a b=\frac{\left(x_{1}^{2}+1\right)^{2}}{4 x_{1}}
$$

一阶导等于零的点为：

$$
S^{\prime}\left(x_{1}\right)=0 \Rightarrow
$$

$$
\frac{2\left(x_{1}^{2}+1\right) \cdot 2 x_{1} \cdot 4 x_{1}-4\left(x_{1}^{2}+1\right)^{2}}{16 x_{1}^{2}}=0 \Rightarrow
$$

$$
16 x_{1}^{2}\left(x_{1}^{2}+1\right)-4\left(x_{1}^{2}+1\right)^{2}=0 \Rightarrow
$$

$$
4 x_{1}^{2}\left(x_{1}^{2}+1\right)-\left(x_{1}^{2}+1\right)^{2}=0
$$

$$
\left(x_{1}^{2}+1\right)\left[4 x_{1}^{2}-\left(x_{1}^{2}+1\right)\right]=0 \Rightarrow
$$

$$
4 x_{1}^{2}=\left(x_{1}^{2}+1\right) \Rightarrow x_{1}^{2}=1 \Rightarrow
$$

$$
x_{1}=\frac{1}{\sqrt{3}}, \ x_{1}=\frac{-1}{\sqrt{3}} \Rightarrow \text{ 舍去 }
$$

接着求解二阶导，只要一阶导中等于零的点在二阶导中大于零，就能说明这是一个极小值点（由于只有 $x = \frac{1}{\sqrt{3}}$ 这一个极值点，因此，在考试的时候，我们可以直接写出 $S^{\prime \prime}\left(\frac{1}{\sqrt{3}}\right) > 0$ 这一个结论——因为 $x = \frac{1}{\sqrt{3}}$ 一定是要找的极小值点）：

$$
S^{\prime}(x)=\frac{2\left(x^{2}+1\right) \cdot 8 x^{2}-4(x+1)^{2}}{16 x^{2}} \Rightarrow
$$

$$
S^{\prime}(x)=\frac{16 x^{2}\left(x^{2}+1\right)-4(x+1)^{2}}{16 x^{2}} \Rightarrow
$$

$$
S^{\prime}(x)=\left(x^{2}+1\right)-\frac{(x+1)^{2}}{4 x^{2}} \Rightarrow
$$

$$
S^{\prime \prime}(x)=2 x-\frac{2(x+1) \cdot 4 x^{2}-8 x(x+1)^{2}}{16 x^{4}}
$$

$$
x=\frac{1}{\sqrt{3}} \Rightarrow
$$

$$
S^{\prime \prime}\left(\frac{1}{\sqrt{3}}\right)=\frac{2}{\sqrt{3}}-\frac{2\left(\frac{1}{\sqrt{3}}+1\right) \cdot \frac{4}{3}-\frac{8}{\sqrt{3}}\left(\frac{1}{\sqrt{3}}+1\right)^{2}}{16 \times \frac{1}{9}}>{0}
$$

于是可知，最小的面积为：

$$
S – \int_{0}^{1} (-x^{2} + 1) \mathrm{~ d} x =
$$

$$
\frac{\left(x_{1}^{2}+1\right)^{2}}{4 x_{1}} – \int_{0}^{1} (-x^{2} + 1) \mathrm{~ d} x =
$$

$$
\frac{4 \sqrt{3}}{9} – \frac{2}{3}.
$$

---