1987 年考研数二真题解析

十、解答题 (本题满分 10 分)

在第一象限内求曲线 $y=-x^{2}+1$ 上的一点, 使该点处的切线与所给曲线及两坐标轴所围 成的图形面积为最小, 并求此最小面积.

根据题目，我们可以绘制出如图 02 所示的示意图：

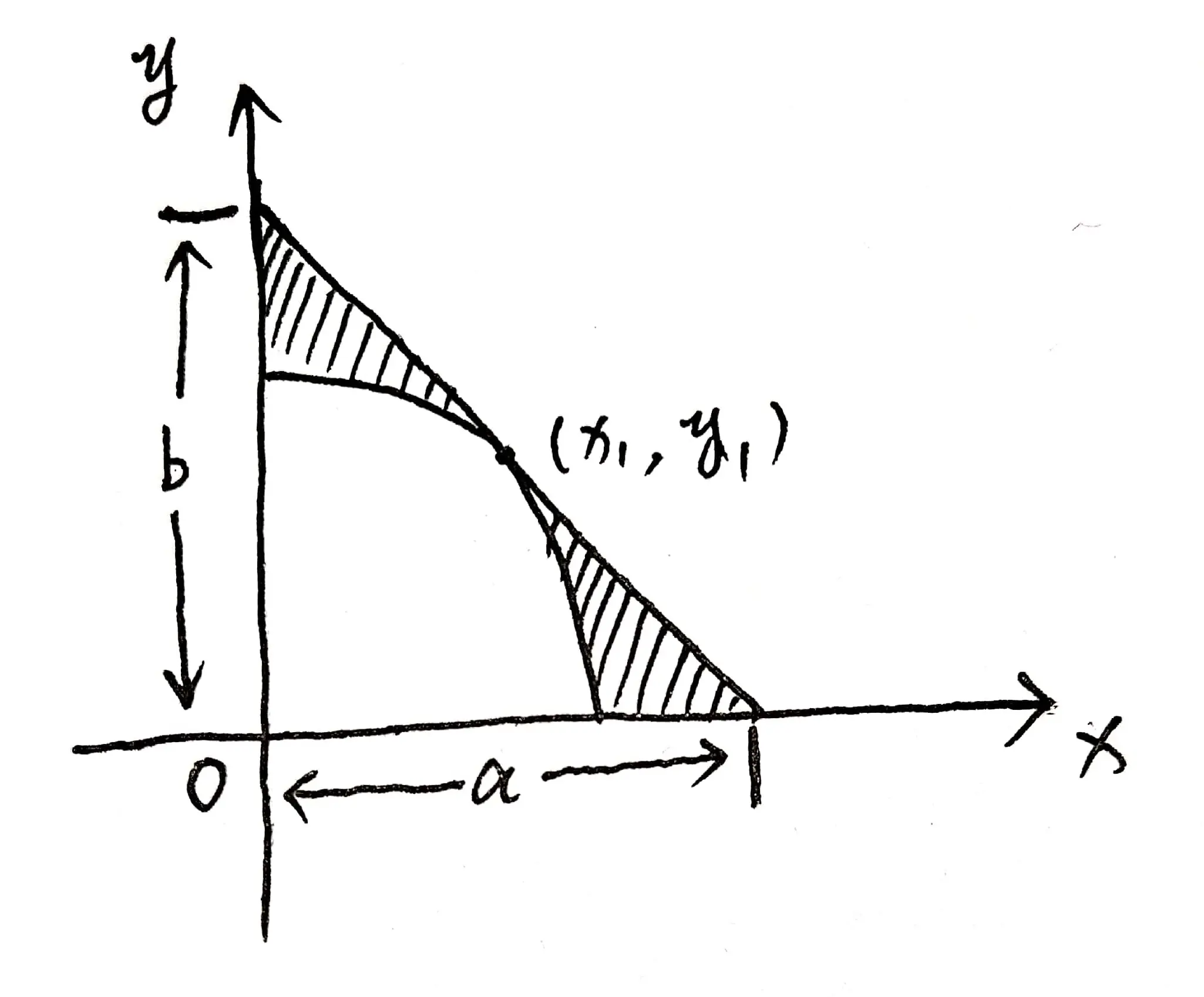
设切点为 $\left(x_{1}, y_{1}\right)$, 则：

$$
y=-x^{2}+1 \Rightarrow y^{\prime}=-2 x \Rightarrow
$$

即斜率为：

$$
k=-2 x_{1}
$$

对应的切线为：

$$
y-y_{1}=-2 x_{1}\left(x-x_{1}\right)
$$

在 $x$ 轴上的截距为：

$$
x=0 \Rightarrow b=y=2 x_{1}^{2}+y_{1}=2 x_{1}^{2}+\left(-x_{1}^{2}+1\right) \Rightarrow
$$

$$
b=x_{1}^{2}+1
$$

在 $y$ 轴上的截距为：

$$
y=0 \Rightarrow-y_{1}=-2 x_{1}\left(a-x_{1}\right) \Rightarrow
$$

$$
-y_{1}=-2 a x_{1}+2 x_{1}^{2} \Rightarrow x_{1}^{2}-1=-2 a x_{1}+2 x_{1}^{2}
$$

$$
2 a x_{1}=x_{1}^{2}+1 \Rightarrow
$$

$$
a=\frac{x_{1}^{2}+1}{2 x_{1}}
$$

于是，要求解的三角形的面积表达式为：

$$
S=\frac{1}{2} a b=\frac{\left(x_{1}^{2}+1\right)^{2}}{4 x_{1}}
$$

一阶导等于零的点为：

$$
S^{\prime}\left(x_{1}\right)=0 \Rightarrow
$$

$$
\frac{2\left(x_{1}^{2}+1\right) \cdot 2 x_{1} \cdot 4 x_{1}-4\left(x_{1}^{2}+1\right)^{2}}{16 x_{1}^{2}}=0 \Rightarrow
$$

$$
16 x_{1}^{2}\left(x_{1}^{2}+1\right)-4\left(x_{1}^{2}+1\right)^{2}=0 \Rightarrow
$$

$$
4 x_{1}^{2}\left(x_{1}^{2}+1\right)-\left(x_{1}^{2}+1\right)^{2}=0
$$

$$
\left(x_{1}^{2}+1\right)\left[4 x_{1}^{2}-\left(x_{1}^{2}+1\right)\right]=0 \Rightarrow
$$

$$
4 x_{1}^{2}=\left(x_{1}^{2}+1\right) \Rightarrow x_{1}^{2}=1 \Rightarrow
$$

$$
x_{1}=\frac{1}{\sqrt{3}}, \ x_{1}=\frac{-1}{\sqrt{3}} \Rightarrow \text{ 舍去 }
$$

接着求解二阶导，只要一阶导中等于零的点在二阶导中大于零，就能说明这是一个极小值点（由于只有 $x = \frac{1}{\sqrt{3}}$ 这一个极值点，因此，在考试的时候，我们可以直接写出 $S^{\prime \prime}\left(\frac{1}{\sqrt{3}}\right) > 0$ 这一个结论——因为 $x = \frac{1}{\sqrt{3}}$ 一定是要找的极小值点）：

$$
S^{\prime}(x)=\frac{2\left(x^{2}+1\right) \cdot 8 x^{2}-4(x+1)^{2}}{16 x^{2}} \Rightarrow
$$

$$
S^{\prime}(x)=\frac{16 x^{2}\left(x^{2}+1\right)-4(x+1)^{2}}{16 x^{2}} \Rightarrow
$$

$$
S^{\prime}(x)=\left(x^{2}+1\right)-\frac{(x+1)^{2}}{4 x^{2}} \Rightarrow
$$

$$
S^{\prime \prime}(x)=2 x-\frac{2(x+1) \cdot 4 x^{2}-8 x(x+1)^{2}}{16 x^{4}}
$$

$$
x=\frac{1}{\sqrt{3}} \Rightarrow
$$

$$
S^{\prime \prime}\left(\frac{1}{\sqrt{3}}\right)=\frac{2}{\sqrt{3}}-\frac{2\left(\frac{1}{\sqrt{3}}+1\right) \cdot \frac{4}{3}-\frac{8}{\sqrt{3}}\left(\frac{1}{\sqrt{3}}+1\right)^{2}}{16 \times \frac{1}{9}}>{0}
$$

于是可知，最小的面积为：

$$
S – \int_{0}^{1} (-x^{2} + 1) \mathrm{~ d} x =
$$

$$
\frac{\left(x_{1}^{2}+1\right)^{2}}{4 x_{1}} – \int_{0}^{1} (-x^{2} + 1) \mathrm{~ d} x =
$$

$$
\frac{4 \sqrt{3}}{9} – \frac{2}{3}.
$$

---