分类： 高等数学

一、题目

${\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}$ $(\frac{\sin x}{1+\cos x}$ $+$ $|x|)$ $dx$ $=$__.

二、解析

本题存在（关于原点对称的）对称区间 “$[-\frac{\pi }{2}$, $\frac{\pi }{2}]$”, 在求积分的时候，如果看到这样的对称区间，则要考虑被积函数是不是奇函数或者偶函数。如果是奇函数，则其在对称区间上的积分为 $0$, 如果是偶函数，则我们可以只计算其大于 $0$ 或者小于 $0$ 方向上的积分，之后再乘以 $2$ 即可获得整个积分区间上的积分数值。

由于：

$\frac{\sin (-x)}{1+\cos (-x)}$ $=$ $\frac{-\sin x}{1+\cos x}$ $\Rightarrow$ $f(-x)$ $=$ $-f(x)$.

因此，$f(x)$ $=$ $\frac{\sin x}{1+\cos x}$ 是一个奇函数，因此，其在对称区间 $[-\frac{\pi }{2}$, $\frac{\pi }{2}]$ 上的积分为 $0$.

又由于：

$|-x|$ $=$ $|x|$ $\Rightarrow$ $g(-x)$ $=$ $g(x)$.

因此，$g(x)$ $=$ $|x|$ 是一个偶函数。

于是：

原式 $=$ ${\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}$ $|x|$ $dx$ $=$ $2$ ${\int }_0^{\frac{\pi }{2}}$ $x$ $dx$ $=$ $2$ $\cdot$ $\frac{1}{2}{x}^2{|}_0^{\frac{\pi }{2}}$ $=$ $\frac{{\pi }^2}{4}$.

当然，本题除了可以使用积分的原理计算之外，还可以画图计算面积，如图 1：

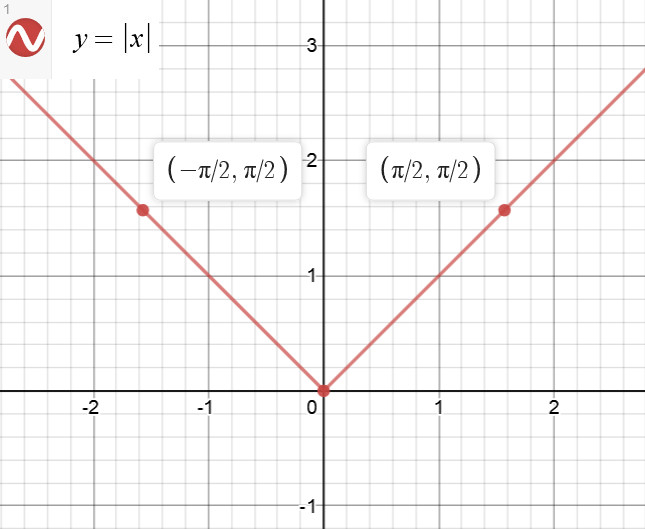
根据上图，我们有：

$\frac{\pi }{2}$ $\cdot$ $\frac{\pi }{2}$ $\cdot$ $\frac{1}{2}$ $\cdot$ $2$ $=$ $\frac{{\pi }^2}{4}$.

综上可知，本题的正确答案是：$\frac{{\pi }^2}{4}$.

EOF

一、题目

$\underset{x\to 0}{lim}$ $(\frac{1-\tan x}{1+\tan x}{)}^{\frac{1}{\sin kx}}$ $=$ $e$, 则 $k$ $=$__.

二、解析

观察本题可以发现，这是一个求极限的式子，而且等式的右边是 $e$, 符合“两个重要极限”中的第二个重要极限的一部分特征。

两个重要极限如下：

$\underset{x\to x_{x_0}}{lim}$ $\frac{\sin x}{x}$ $=$ $1$, $\underset{x\to 0}{lim}$ $(1+x{)}^{\frac{1}{x}}$ $=$ $\underset{x\to \mathrm{\infty }}{lim}$ $(1+\frac{1}{x}{)}^x$ $=$ $e$.

由于题目中的式子不存在上述公式中的 $1$, 因此，我们需要构造出这个 $1$, 即：

$1$ $+$ $◻$ $=$ $\frac{1-\tan x}{1+\tan x}$ $\Rightarrow$ $◻$ $=$ $\frac{1-\tan x}{1+\tan x}$ $-$ $1$ $=$ $\frac{1-\tan x}{1+\tan x}$ $-$ $\frac{1+\tan x}{1+\tan x}$ $=$ $\frac{-2\tan x}{1+\tan x}$.

于是，原式 $=$ $\underset{x\to 0}{lim}$ $(1+\frac{-2\tan x}{1+\tan x}{)}^{\frac{1}{\sin kx}}$ $=$ $e$. (1)

由于当 $x$ $\to$ $0$ 时，$\frac{-2\tan x}{1+\tan x}$ $\to$ $0$ 且 $\frac{1}{\sin kx}$ $\to$ $\mathrm{\infty }$, 所以，符合使用“两个重要极限”的条件，可以继续接下来的计算。

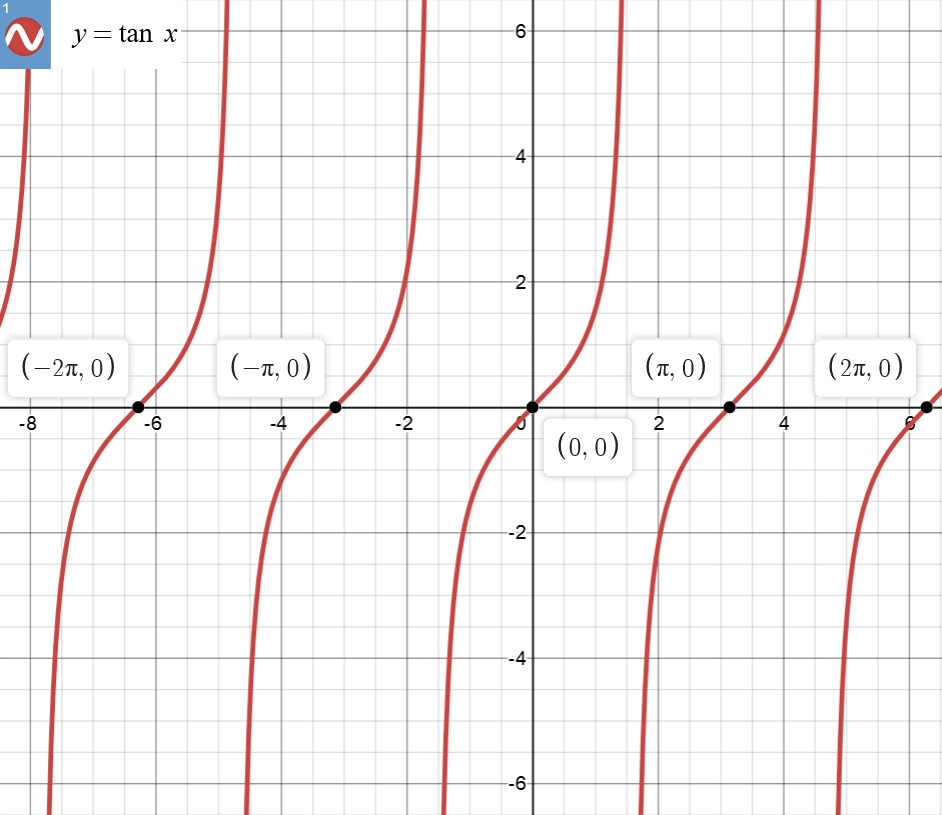
接下来继续向公式的方向构造等式。

$(1)$ $=$ $\underset{x\to 0}{lim}$ $(1+\frac{-2\tan x}{1+\tan x}{)}^{\frac{1+\tan x}{-2\tan x}\frac{-2\tan x}{1+\tan x}\frac{1}{\sin kx}}$. (2)

根据公式，我们知道：

$\underset{x\to 0}{lim}$ $(1+\frac{-2\tan x}{1+\tan x}{)}^{\frac{1+\tan x}{-2\tan x}}$ $=$ $e$.

于是：

$(2)$ $=$ $e^{\underset{x\to 0}{lim}\frac{-2\tan x}{1+\tan x}\frac{1}{\sin kx}}$ $=$ $e^{\underset{x\to 0}{lim}\frac{-2\tan x}{(1+\tan x)\sin kx}}$. (3)

当 $x$ $\to$ $0$ 时，$\tan x$ $\to$ $0$ 是不可以带入原式中的（只有非零和非无穷的数值可以带入原式中。），不过当 $x$ $\to$ $0$ 时，$(1+\tan x)$ $\to$ $1$ 是可以带入原式中的，于是：

$\underset{x\to 0}{lim}$ $\frac{-2\tan x}{(1+\tan x)\sin kx}$ $=$ $\underset{x\to 0}{lim}$ $\frac{-2\tan x}{\sin kx}$.

又因为当 $x$ $\to$ $0$ 时，$\sin x$ $\sim$ $\tan x$ $\sim x$, 于是：

$\underset{x\to 0}{lim}$ $\frac{-2\tan x}{\sin kx}$ $=$ $\underset{x\to 0}{lim}$ $\frac{-2x}{kx}$ $=$ $-\frac{2}{k}$.

即：

$e^{-\frac{2}{k}}$ $=$ $e$ $\Rightarrow$ $-$ $\frac{2}{k}$ $=$ $1$ $\Rightarrow$ $k$ $=$ $-$ $2$.

综上可知，正确答案是：$-2$.

EOF

一、题目

设函数 $f(x)$ $=$ $x$ $+$ $a$ $\ln (1+x)$ $+$ $bx$ $\sin x$, $g(x)$ $=$ $k$ $x^3$ 在 $x$ $\to$ $0$ 时等价无穷小，求常数 $a$, $b$, $k$ 的取值.

二、解析

由于 $x$ $\to$ $0$ 时，$f(x)$ 和 $g(x)$ 是等价无穷小，因此有：

$\underset{x\to 0}{lim}$ $\frac{f(x)}{g(x)}$ $=$ $1$, 即：

$\underset{x\to 0}{lim}$ $\frac{x+a\ln (1+x)+bx\sin x}{k{x}^3}$ $=$ $1$.

又由麦克劳林公式：

1. $\sin x$ $=$ $x$ $+$ $o(x^2)$;

注 1：
根据麦克劳林公式，$\sin x$ 也可以等于 $x$ $-$ $\frac{x^3}{6}$ $+$ $o(x^4)$, 但是这里为了能够在接下来的计算中使得分子分母可以使用“对照”的方式求解，分子的最大幂次不能大于分母的最大幂次。由于 $\sin x$ 在使用麦克劳林公式替换之后还需要和 $x$ 相乘得到二次幂，因此这里只能令 $\sin x$ 等于 $x$ $+$ $o(x^2)$.

2. $\ln (1+x)$ $=$ $x$ $-$ $\frac{x^2}{2}+\frac{x^3}{3}$ $+$ $o(x^3)$.

注 2：
对 $\ln (1+x)$ 项数的选取所依据的原因和注 $1$ 一致。

于是，我们有：

$1$ $=$ $\underset{x\to 0}{lim}$ $\frac{x+ax-\frac{a}{2}{x}^2+\frac{a}{3}{x}^3+o(x^3)+b{x}^2+o(x^3)}{k{x}^3}$ $=$ $\underset{x\to 0}{lim}$ $\frac{(1+a)x+(b-\frac{a}{2})x^2+\frac{a}{3}{x}^3+o(x^3)}{k{x}^3}$.

于是，我们有：

$\{\begin{array}{c}1+a=0,\\ b-\frac{a}{2}=0,\\ \frac{a}{3}=k.\end{array}$

解得：

$\{\begin{array}{c}a=-1,\\ b=-\frac{1}{2},\\ k=-\frac{1}{3}.\end{array}$

三、手写作答

EOF