题目
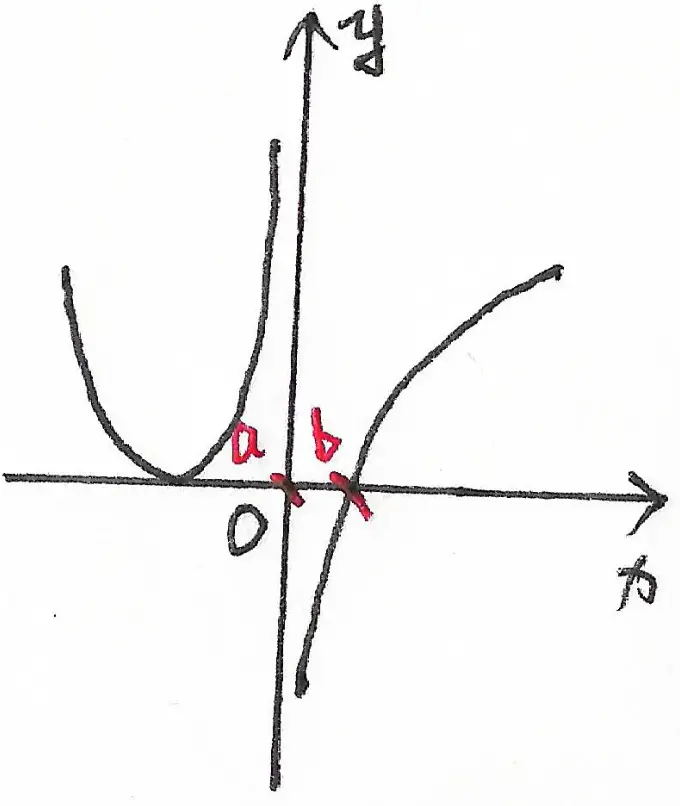
设函数 $f(x)$ 在 $(- \infty, +\infty)$ 内连续,其二阶导数 $f^{”}(x)$ 的图形如图 1 所示,则曲线 $y=f(x)$ 的拐点的个数为 $?$
$$
A. 0
$$
$$
B. 1
$$
$$
C. 2
$$
$$
D. 3
$$
解析
本题就是考察拐点的性质:
- 拐点是原函数的凹凸性发生改变的点;
- 拐点是一阶导函数的增减发生改变的点;
- 拐点是二阶导函数的正负发生改变的点。
扩展:极值点的性质:
- 极值点是原函数的增减发生改变的点;
- 极值点是一阶导函数的正负发生改变的点。
由于题中给出的就是二阶导函数的函数图像,因此,我们观察图中哪些点的两侧该函数图像的正负发生改变了即可找到拐点。
又由于 $f(x)$ 在 $(- \infty, + \infty)$ 上有有定义,因此,$f(x)$ 在 $x=0$ 这一点处也有定义。于是,我们可以在图中找到 $a$, $b$ 两个点,他们左右两侧的二阶导函数值的正负发生了改变,如图 1。因此,拐点的个数为 $2$.
综上可知,正确选项为 $C$.
EOF