一、题目
下列命题中正确的是()
( A ) 若 $\lim_{x \rightarrow x_{0}}$ $f(x)$ $\geqslant$ $\lim_{x \rightarrow x_{0}}$ $g(x)$, 则 $\exists$ $\varepsilon$ $>$ $0$, 当 $0$ $<$ $|x-x_{0}|$ $<$ $\varepsilon$ 时,$f(x)$ $\geqslant$ $g(x)$.
( B ) 若 $\exists$ $\varepsilon$ $>$ $0$, 当 $0$ $<$ $|x-x_{0}|$ $<$ $\varepsilon$ 时,$f(x)$ $>$ $g(x)$, 且 $\lim_{x \rightarrow x_{0}}$ $f(x)$ $=$ $A_{0}$, $\lim_{x \rightarrow x_{0}}$ $g(x)$ $=$ $B_{0}$, 则 $A_{0}$ $>$ $B_{0}$.
( C ) 若 $\exists$ $\varepsilon$ $>$ $0$, 当 $0$ $<$ $|x-x_{0}|$ $<$ $\varepsilon$ 时,$f(x)$ $>$ $g(x)$, 则 $\lim_{x \rightarrow x_{0}}$ $f(x)$ $\geqslant$ $\lim_{x \rightarrow x_{0}}$ $g(x)$.
( D ) 若 $\lim_{x \rightarrow x_{0}}$ $f(x)$ $>$ $\lim_{x \rightarrow x_{0}}$ $g(x)$, 则 $\exists$ $\varepsilon$ $>$ $0$, 当 $0$ $<$ $|x-x_{0}|$ $<$ $\varepsilon$ 时,$f(x)$ $>$ $g(x)$.
二、解析
概念考察题是考研数学中一类比较难的题,这类题的难点在于除了紧抠概念之外,解答者没有多少可以自由发挥的空间。而且,概念考察题考察的都是概念的细微之处,一不留神就可能审错题。
从本题的四个选项可以看出,本题考查的着重点在函数极限这一部分。更细致的来看,本题考查了函数极限的定义中当 $x$ $\rightarrow$ $x_{0}$ 时的极限的定义,如下:
已知 $\lim_{x \rightarrow x_{0}}$ $f(x)$ $=$ $A$
任给 $\varepsilon$ $>$ $0$, 存在正数 $\delta$, 当 $0$ $<$ $(x$ $-$ $x_{0})$ $<$ $\delta$ 时,就有 $|f(x)-A|$ $<$ $\varepsilon$.
注:上面这个定义说的通俗一点就是,当 $x$ 与 $x_{0}$ 足够接近的时候,$f(x)$ 与 $f(x)$ 的极限 $A$ 也足够接近。
本题还考察了函数极限的性质中的“保号性”,如下:
设 $\lim$ $f(x)$ $=$ $A$ $>$ $0$, 则在极限管辖的范围内,$f(x)$ $>$ $0$ $($ $f(x)$ $>$ $\frac{A}{2}$ $)$.
反之,$f(x)$ $>$ $0$ 且 $\lim$ $f(x)$ $=$ $A$ $\Rightarrow$ $A$ $\geqslant$ $0$.
注:当 $x$ $\rightarrow$ $x_{0}$ 时,“极限管辖的范围”指的就是 $x_{0}$ 的去心邻域;当 $x$ $\rightarrow$ $\infty$ 时,“极限管辖的范围”指的就是无穷远处。
对于函数极限的性质中的保号性,我们需要明确以下几点:
- 解答保号性问题的大前提是“涉及到的函数的极限均存在”,这也是解决所有涉及极限的问题的大前提:要研究和利用极限,则极限必须存在;
- 保号性都是局部保号性,即只有在极限管辖的范围内才存在保号性;
- 由极限大于 $0$ 可以推出函数大于 $0$, 不能推出函数等于 $0$ 或者函数小于 $0$. 由函数大于 $0$ 可以推出极限大于 $0$ 或者极限等于 $0$, 而且在不确定极限究竟是只大于 $0$ 还是只小于 $0$ 的情况下,要写成极限大于等于 $0$ 的形式。
以下是对本题中每一个选项的分析。
A 选项
该选项给出了:
$\lim_{x \rightarrow x_{0}}$ $f(x)$ $\geqslant$ $\lim_{x \rightarrow x_{0}}$ $g(x)$.
这说明 $f(x)$ 和 $g(x)$ 的极限都存在(满足了研究极限问题的大前提,条件可用,可以继续接下来的思考步骤)且 $f(x)$ 的极限大于等于 $f(x)$ 的极限。
于是,我们有:
$\lim_{x \rightarrow x_{0}}$ $($ $f(x)$ $-$ $g(x)$ $)$ $\geqslant$ $0$.
接下来选项给出了:
若 $\exists$ $\varepsilon$ $>$ $0$, 当 $0$ $<$ $|x-x_{0}|$ $<$ $\varepsilon$ 时
这说明我们是要在“函数极限的管辖范围内”讨论这个选项的说法,具备使用保号性的前提,条件可用,可以继续接下来的思考步骤。
该选项接下来指出,由上面的条件可以推出 $f(x)$ $\geqslant$ $g(x)$.
这个结论是不对的。原因如下:
若函数 $f(x)$ 的极限 $A$ $>$ $0$, 则可以推出函数 $f(x)$ $>$ $0$;
若函数 $f(x)$ 的极限 $A$ $<$ $0$, 则可以推出函数 $f(x)$ $<$ $0$;
若函数 $f(x)$ 的极限 $A=0$, 则不能确定函数 $f(x)$ 是大于 $0$, 小于 $0$ 还是等于 $0$. 原因是,如果 $A$ $=$ $0$ 我们不知道函数 $f(x)$ 是在大于 $0$ 的方向上趋近于极限 $A$, 还是在小于 $0$ 的方向上趋近于极限 $A$, 抑或 $f(x)$ $=$ $0$.
如图 1 所示,当函数的极限等于 $0$ 时,函数可能是大于 $0$ 的:
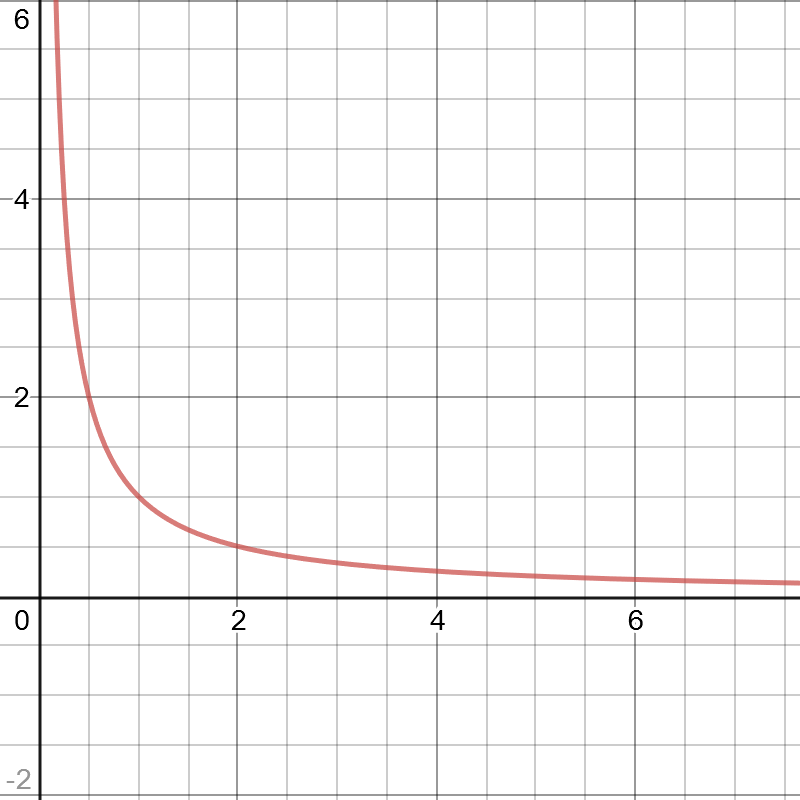
如图 2 所示,当函数的极限等于 $0$ 时,函数也可能是小于 $0$ 的:
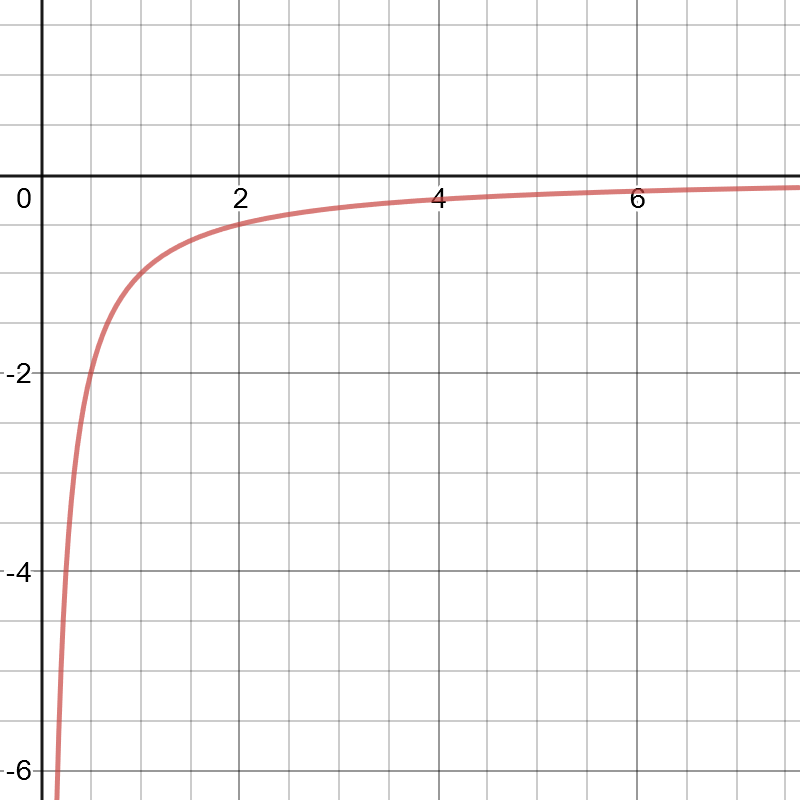
第三种情况,当函数的极限等于 $0$ 时,函数可能也是等于 $0$ 的,如图 3 所示:
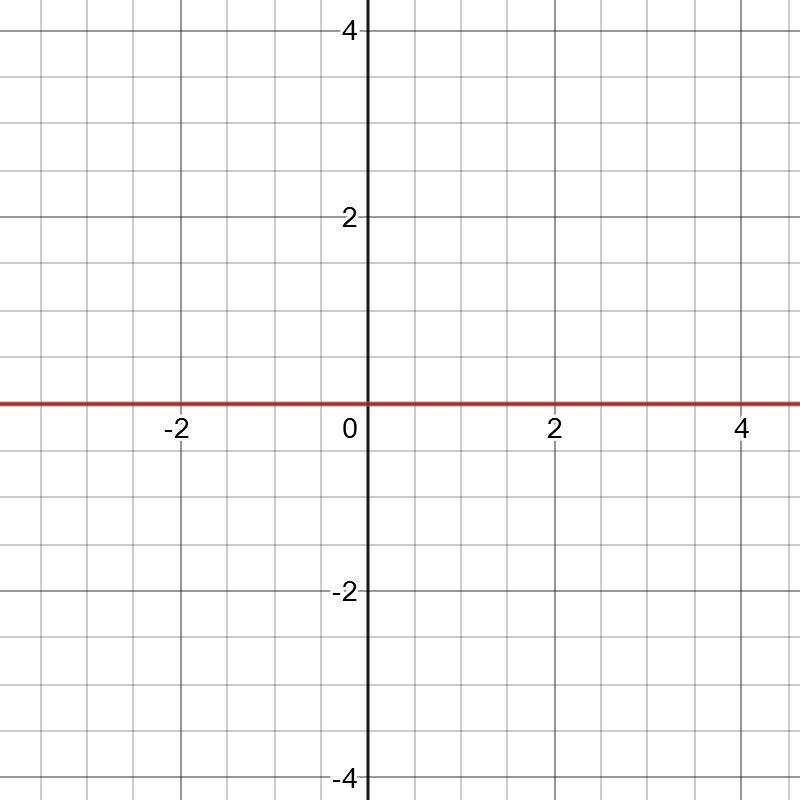
因此,已知极限 $\lim_{x \rightarrow x_{0}}$ $[$ $f(x)$ $-$ $g(x)$ $]$ $\geqslant$ $0$, 并不能推导出函数 $F(x)$ $=$ $[$ $f(x)$ $-$ $g(x)$ $]$ $\geqslant$ $0$.
综上可知,选项 A 是错误的。
B 选项
题目中给出了如下条件:
若 $\exists$ $\varepsilon$ $>$ $0$, 当 $0$ $<$ $|x-x_{0}|$ $<$ $\varepsilon$ 时
因此,本题符合函数极限保号性的使用条件,条件可用,可以继续接下来的思考步骤。
接着,该选项给出:
$f(x)$ $>$ $g(x)$
于是,当我们令 $F(x)$ $=$ $f(x)$ $-$ $g(x)$ 时,可以得出如下结论:
$F(x)$ $>$ $0$
接着,该选项又给出:
$\lim_{x \rightarrow x_{0}}$ $f(x)$ $=$ $A_{0}$, $\lim_{x \rightarrow x_{0}}$ $g(x)$ $=$ $B_{0}$
这说明函数 $f(x)$ 和函数 $g(x)$ 都是存在极限的,符合我们研究函数极限问题的大前提,条件可用,可以继续接下来的思考步骤。
最后,该选项给出了他的结论:
$A_{0}$ $>$ $B_{0}$
有了这个结论,结合前面的条件,我们可以把该选项改写成如下形式:
已知函数 $F(x)$ 存在极限,且函数 $F(x)$ $>$ $0$, 则 $\lim_{x \rightarrow x_{0}}$ $F(x)$ $>$ $0$.
这个结论显然是错误的,因为已知函数大于 $0$ 的时候,其极限是可能等于 $0$ 的,例如对 A 选项的解析中给出的图 1, 函数 $f(x)$ $=$ $\frac{1}{x}$ 始终是大于 $0$ 的,但是其极限却是等于 $0$ 的。
综上可知,选项 B 是错误的。
C 选项
该选项的错误比较明显,因为选项中没有指明函数 $f(x)$ 和函数 $g(x)$ 的极限存在,缺少了研究极限问题的大前提,那么,接下来的所有说明和结论都是没有根据也没有意义的。不过,如果 C 选项像 B 选项一样指明函数 $f(x)$ 和函数 $g(x)$ 的极限是存在的,那么该选项的表述就是正确的,原因在 B 选项中已经分析过。
综上可知,选项 C 是错误的。
D 选项
该选项首先给出了如下条件:
$\lim_{x \rightarrow x_{0}}$ $f(x)$ $>$ $\lim_{x \rightarrow x_{0}}$ $g(x)$
若我们令 $F(x)$ $=$ $f(x)$ $-$ $g(x)$, 则上面的条件可以改写成:
$\lim_{x \rightarrow x_{0}}$ $F(x)$ $>$ $0$
接着选项给出了:
若 $\exists$ $\varepsilon$ $>$ $0$, 当 $0$ $<$ $|x-x_{0}|$ $<$ $\varepsilon$ 时
这说明我们是要在“函数极限的管辖范围内”讨论这个选项的说法,具备使用保号性的前提,条件可用,可以继续接下来的思考步骤。
接着,该选项给出了它的结论:
$f(x)$ $>$ $g(x)$
根据前面的分析可知,我们可以将此改写成:
$F(x)$ $>$ $0$
我们知道,当一个函数的极限存在且大于 $0$ 的时候,在函数极限的管辖范围内,可以推导出该函数也大于 $0$.
综上可知,选项 D 是正确的。
EOF