题目
设平面区域 $D=$ $\{(x,y)|$ $1 \leqslant x^{2} + y^{2} \leqslant 4$, $x \geqslant 0$, $y \geqslant 0 \}$, 计算:
$$
\iint_{D} \frac{x \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} dxdy.
$$
解析
根据题目可知,积分区域 $D$ 是由两个圆心坐标均为 $(0,0)$, 半径分别为 $1$ 和 $2$ 的两个同心圆在直角坐标系的第一象限中围成的,如图 01 所示:
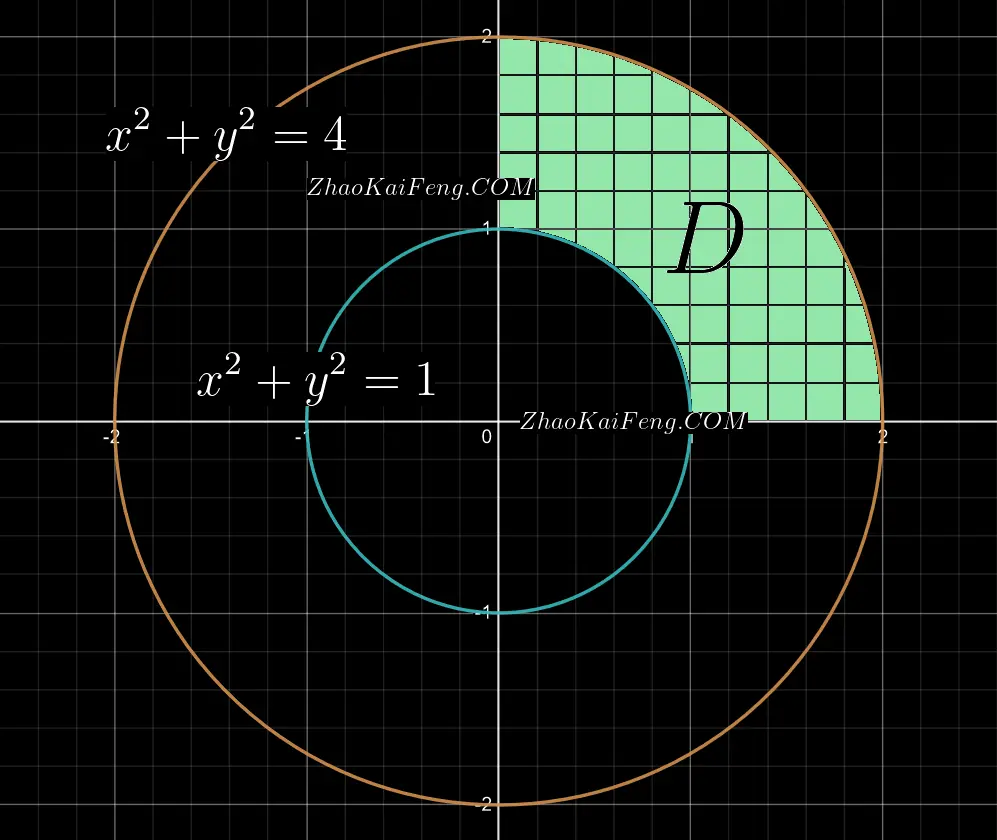
方法一
由于积分区域 $D$ 是关于直线 $x=y$ 对称的,因此,若令:
$$
I = \iint_{D} \frac{x \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} dxdy.
$$
则:
$$
I = \iint_{D} \frac{y \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} dxdy.
$$
于是:
$$
I=
$$
$$
\frac{1}{2}[\iint_{D} \frac{x \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} dxdy + \iint_{D} \frac{y \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} dxdy] \Rightarrow
$$
$$
I = \frac{1}{2} \iint_{D} \frac{(x+y) \sin (\pi \sqrt{x^{2} + y^{2}})}{x+y} \Rightarrow
$$
$$
I = \frac{1}{2} \iint_{D} \sin (\pi \sqrt{x^{2} + y^{2}}) \Rightarrow 转化为极坐标系 \Rightarrow
$$
$$
I = \frac{1}{2} \iint_{D} \sin (\pi r) \cdot r dr d \theta \Rightarrow
$$
$$
I = \frac{1}{2} \int_{0}^{\frac{\pi}{2}} d \theta \int_{1}^{2} r \sin (\pi r) dr.
$$
其中:
$$
\frac{1}{2} \int_{0}^{\frac{\pi}{2}} d \theta = \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4}.
$$
$$
\int_{1}^{2} r \sin (\pi r) dr =
$$
$$
\frac{1}{\pi^{2}} \int_{\pi}^{2\pi} (\pi r) \sin (\pi r) d(\pi r) =
$$
$$
\frac{1}{\pi^{2}} \int_{\pi}^{2\pi} A \sin A d A =
$$
$$
\frac{-1}{\pi^{2}} \int_{\pi}^{2 \pi} A d(\cos A) \Rightarrow
$$
$$
\frac{-1}{\pi^{2}} [A \cos A |_{\pi}^{2 \pi} – \int_{\pi}^{2 \pi} \cos A dA] \Rightarrow
$$
$$
\frac{-1}{\pi^{2}} [A \cos A |_{\pi}^{2 \pi} – \sin A|_{\pi}^{2 \pi}] \Rightarrow
$$
$$
\frac{-1}{\pi^{2}} [2 \pi + \pi – 0] = \frac{-3}{\pi}.
$$
于是:
$$
I = \frac{1}{2} \int_{0}^{\frac{\pi}{2}} d \theta \int_{1}^{2} r \sin (\pi r) dr \Rightarrow
$$
$$
I = \frac{\pi}{4} \cdot \frac{-3}{\pi} = \frac{-3}{4}.
$$
方法二
$$
\iint_{D} \frac{x \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} r d \theta dr \Rightarrow 转化为极坐标系 \Rightarrow
$$
$$
\iint_{D} \frac{r \cos \theta \sin (\pi r)}{r \cos \theta + r \sin \theta} r d \theta dr \Rightarrow
$$
$$
\iint_{D} \frac{\cos \theta \sin (\pi r)}{ \sin \theta + \cos \theta} r d \theta d r \Rightarrow
$$
$$
\int_{0}^{\frac{\pi}{2}} \frac{\cos \theta}{\sin \theta + \cos \theta} \int_{1}^{2} r \sin (\pi r) dr.
$$
其中,由【方法一】可知:
$$
\int_{1}^{2} r \sin (\pi r) dr = \frac{-3}{\pi}.
$$
又由于,在 $(0, \frac{\pi}{2})$ 内,$\sin \theta$ 和 $\cos \theta$ 的图象是关于直线 $x = \frac{\pi}{4}$ 对称的,因此:
$$
\int_{0}^{\frac{\pi}{2}} \frac{\cos \theta}{\sin \theta + \cos \theta} d \theta = \int_{0}^{\frac{\pi}{2}} \frac{\sin \theta}{\sin \theta + \cos \theta} d \theta
$$
于是:
$$
\int_{0}^{\frac{\pi}{2}} \frac{\cos \theta}{\sin \theta + \cos \theta} d \theta =
$$
$$
\frac{1}{2} [ \int_{0}^{\frac{\pi}{2}} \frac{\cos \theta}{\sin \theta + \cos \theta} d \theta + \int_{0}^{\frac{\pi}{2}} \frac{\sin \theta}{\sin \theta + \cos \theta} d \theta ] =
$$
$$
\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \frac{\sin \theta + \cos \theta}{\sin \theta + \cos \theta} d \theta =
$$
$$
\frac{1}{2} \int_{0}^{\frac{\pi}{2}} 1 d \theta = \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4}.
$$
于是:
$$
\iint_{D} \frac{x \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} r d \theta dr =
$$
$$
\frac{-3}{\pi} \cdot \frac{\pi}{4} = \frac{-3}{4}.
$$
补充
除了上面所示的计算 $\int_{0}^{\frac{\pi}{2}} \frac{\cos \theta}{\sin \theta + \cos \theta} d \theta$ 的方式之外,还可以用如下方式完成对 $\int_{0}^{\frac{\pi}{2}} \frac{\cos \theta}{\sin \theta + \cos \theta} d \theta$ 的求解。
$$
\int_{0}^{\frac{\pi}{2}} \frac{\cos \theta}{\sin \theta + \cos \theta} d \theta =
$$
$$
\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \frac{\cos \theta + \sin \theta + \cos \theta – \sin \theta}{\cos \theta + \sin \theta} d \theta =
$$
$$
\frac{1}{2} [\int_{0}^{\frac{\pi}{2}} \frac{\cos \theta + \sin \theta}{\cos \theta + \sin \theta} d \theta + \frac{\cos \theta – \sin \theta}{\cos \theta + \sin
\theta}] =
$$
$$
\frac{1}{2} [\int_{0}^{\frac{\pi}{2}} 1 d \theta + \frac{\cos \theta – \sin \theta}{\cos \theta + \sin
\theta}] =
$$
$$
\frac{1}{2} [\int_{0}^{\frac{\pi}{2}} 1 d \theta + \ln |\cos \theta + \sin
\theta| |_{0}^{\frac{\pi}{2}}] =
$$
$$
\frac{1}{2} [\frac{\pi}{2} + \ln(0+1) – \ln (1+0)] =
$$
$$
\frac{1}{2} [\frac{\pi}{2} + 0 – 0] = \frac{\pi}{4}.
$$
