连续函数的导数不一定连续：导函数的间断点只可能是震荡间断点

一、题目

已知，函数 $f(x)$ 在 $(a, b)$ 内可导，$x_{0} \in(a, b)$ 是 $f^{\prime}(x)$ 的间断点，则该间断点一定是什么类型的间断点？

难度评级：

二、解析

【间断点的分类】

第一类间断点：

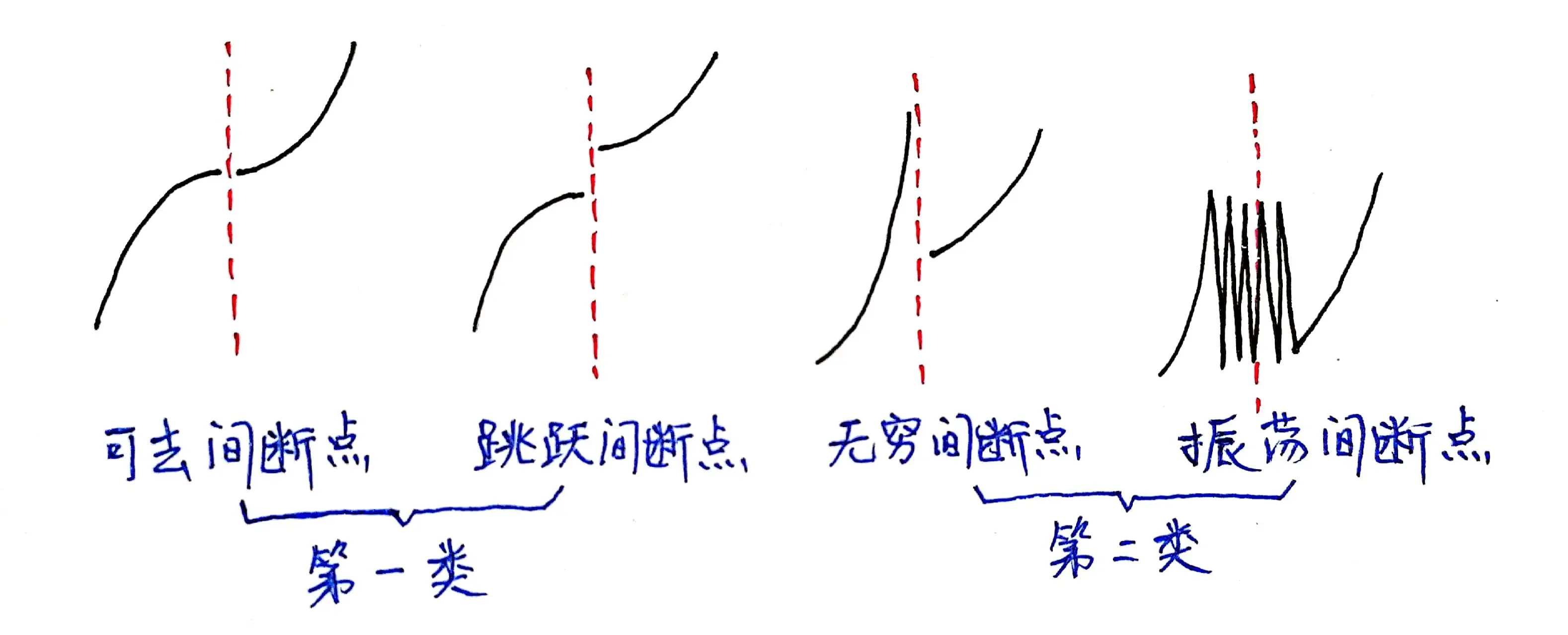
• 可去间断点（函数在该点处无定义，但是该点左右两侧的极限相等）
• 跳跃间断点（函数在该点处无定义，且该点左右两侧的极限不相等）

第二类间断点：

• 无穷间断点（该点左右两侧至少有一侧的极限是趋于无穷大的）
• 震荡断点（函数在该点处震荡无极限）

示意图：

方法一：用函数图像的性质推导

由于可导必连续，因此，若函数 $f(x)$ 在 $(a, b)$ 内可导，则，函数 $f(x)$ 在 $(a, b)$ 内连续。

而连续函数的导数对应的斜率一定是连续改变的，不可能形成“清晰的间断”，因此也就不可能是可去间断点、跳跃间断点和无穷间断点。

但是，震荡间断点虽然也是间断点，但由于在无穷的作用下会变得非常“紧密”，以至于接近能体现出连续性质的“致密”，不会存在清晰的间断点，因此连续函数的导数有可能存在震荡间断点，例如函数 $f(x)=\left\{\begin{array}{cl}x^{2} \sin \frac{1}{x}, & x \neq 0 \\ 0, & x=0\end{array}\right.$ 的导函数 $f^{\prime}(x)=\left\{\begin{array}{c}2 x \sin \frac{1}{x}-\cos \frac{1}{x}, x \neq 0 \\ 0, x=0 .\end{array}\right.$ 就具有此类性质。

$f(x)=\left\{\begin{array}{cl}x^{2} \sin \frac{1}{x}, & x \neq 0 \\ 0, & x=0\end{array}\right.$ 的函数图像如下（在 $x = 0$ 附近有界震荡连续）：

$f^{\prime}(x)=\left\{\begin{array}{c}2 x \sin \frac{1}{x}-\cos \frac{1}{x}, x \neq 0 \\ 0, x=0 .\end{array}\right.$ 的函数图像如下（在 $x = 0$ 附近有界震荡间断）：

方法二：用间断点的性质推导

由于函数间断点的类型一定是和该函数在一点处左右两侧的极限有关的，因此，判断函数 $f^{\prime}(x)$ 在 $x = x_{0}$ 处的间断点类型就是对 $\lim_{x \rightarrow x_{0}^{+}} f^{\prime}(x)$ 和 $\lim_{x \rightarrow x_{0}^{-}} f^{\prime}(x)$ 进行讨论。

首先，假设：

$$
\lim \limits_{x \rightarrow x_{0}^{+}} f^{\prime}(x)=\lim \limits_{x \rightarrow x_{0}^{-}} f^{\prime}(x)=K
$$

则：

$$
f^{\prime}\left(x_{0}^{+}\right)=\lim \limits_{x \rightarrow x_{0}^{+}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \Rightarrow \frac{0}{0} \ 型极限 \Rightarrow
$$

洛必达运算：

$$
\lim \limits_{x \rightarrow x_{0}^{+}} f^{\prime}(x)= K
$$

又：

$$
f^{\prime}\left(x_{0}^{-}\right)=\lim \limits_{x \rightarrow x_{0}^{-}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \Rightarrow \frac{0}{0} \ 型极限 \Rightarrow
$$

$$
\lim \limits_{x \rightarrow x_{0}^{-}} f^{\prime}(x)=K
$$

于是：

$$
f^{\prime}\left(x_{0}^{+}\right)=f^{\prime}\left(x_{0}^{-}\right) =K
$$

又由于导数 $f^{\prime}(x)$ 存在，因此 $f^{\prime}(x_{0})$ 一定存在，即：

$$
f^{\prime}\left(x_{0}\right) = K
$$

因此：

$$
\lim \limits_{x \rightarrow x_{0}} f^{\prime}(x)=f^{\prime}\left(x_{0}\right)
$$

因此，函数 $f^{\prime}(x)$ 在点 $x = x_{0}$ 处连续，不存在间断点，进而可知，函数 $f^{\prime}(x)$ 不可能存在可去间断点与跳跃间断点。

接着，若：

$$
\lim \limits_{x \rightarrow x_{0}^{+}} f^{\prime}(x)=\infty \Rightarrow \lim \limits_{x \rightarrow x_{0}^{+}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \Rightarrow \text { 洛必达运算 } \Rightarrow
$$

$$
\lim \limits_{x \rightarrow x_{0}^{+}} f^{\prime}(x)=\infty \Rightarrow \text{不存在}
$$

$$
\lim \limits_{x \rightarrow x_{0}^{-}} f^{\prime}(x)=\infty \Rightarrow \lim \limits_{x \rightarrow x_{0}^{-}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \Rightarrow \text { 洛必达运算 } \Rightarrow
$$

$$
\lim \limits_{x \rightarrow x_{0}^{-}} f^{\prime}(x)=\infty \Rightarrow \text{不存在}
$$

上面的计算结果都与函数 $f^{\prime}(x)$ 在点 $x = x_{0}$ 处存在相矛盾，因此，函数 $f^{\prime}(x)$ 的间断点也不可能是无穷间断点。

综上，函数 $f^{\prime}(x)$ 的间断点只可能是震荡间断点（第二类间断点）。

---