判断一个点是否是间断点不能只看该点处的情况，还要看该点周围的情况

一、题目

已知 $f(x)$ 与 $g(x)$ 在 $(-\infty,+\infty)$ 内都有定义，且 $x=x_{1}$ 是 $f(x)$ 的唯一间断点, $x=$ $x_{2}$ 是 $g(x)$ 的唯一间断点. 则 $x = 1$ 和 $x = -1$ 分别是该函数的什么间断点？

难度评级：

二、解析

首先，将函数 $f(x)$ 写成分段函数：
$$
f(x)=\lim \limits_{n \rightarrow \infty} \frac{x^{2 n}-1}{x^{2 n}+1} \Rightarrow
$$

$$
f(x)=\left\{\begin{array}{cc}1 & |x|>1, \\ 0 & |x|=1, \\ -1 & |x|<1. \end{array}\right.
$$

接着，我们可以将函数 $f(x)$ 写成如下形式：

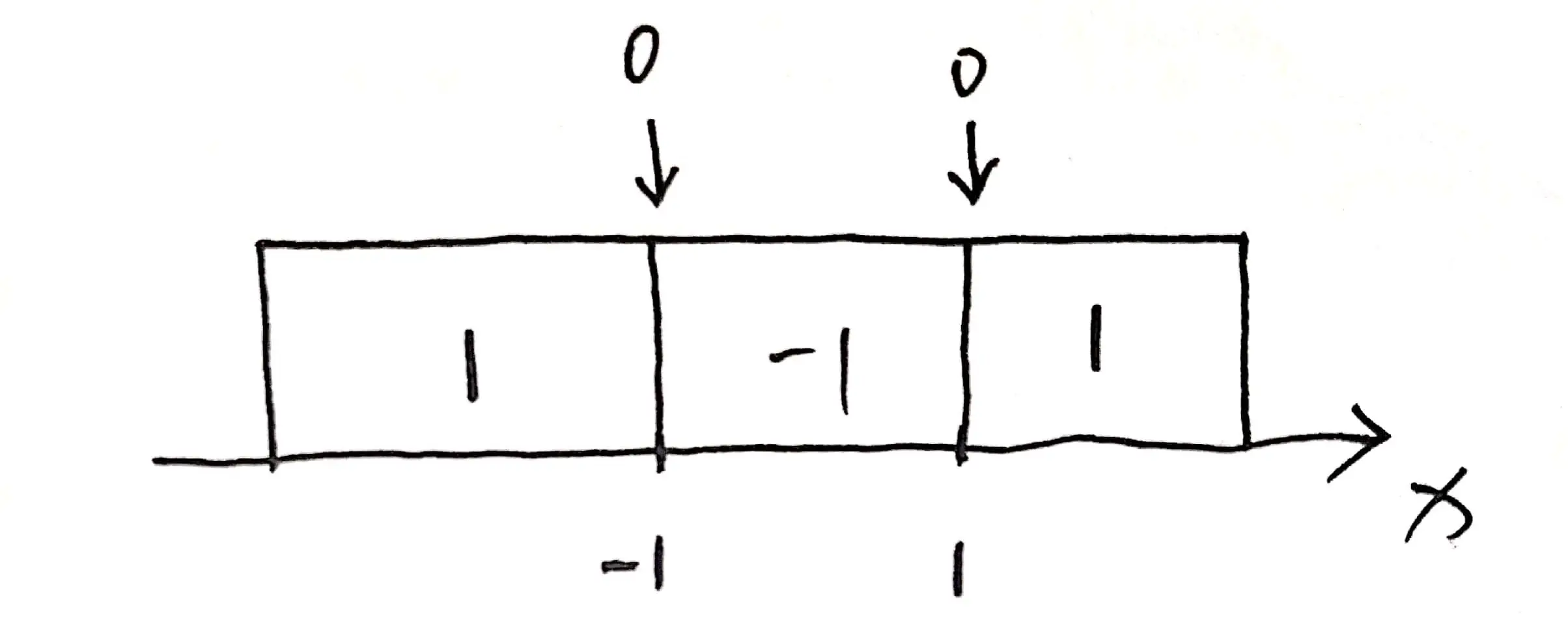
于是：

$$
\lim \limits_{x \rightarrow 1^{+}} f(x)=1 \quad \lim \limits_{x \rightarrow 1^{-}} f(x)=-1 \ \Rightarrow
$$

$$
\lim \limits_{x \rightarrow 1^{+}} f(x) \neq \lim \limits_{x \rightarrow 1^{-}} f(x)
$$

$$
\lim \limits_{x \rightarrow-1^{+}} f(x)=-1 \quad \lim \limits_{x \rightarrow-1^{-}} f(x)=1 \ \Rightarrow
$$

$$
\lim \limits_{x \rightarrow-1^{+}} f(x) \neq \lim \limits_{x \rightarrow-1^{-}} f(x)
$$

于是可知，$x = 1$ 和 $x = -1$ 的左右极限都存在，是第一类间断点。

---