一、题目
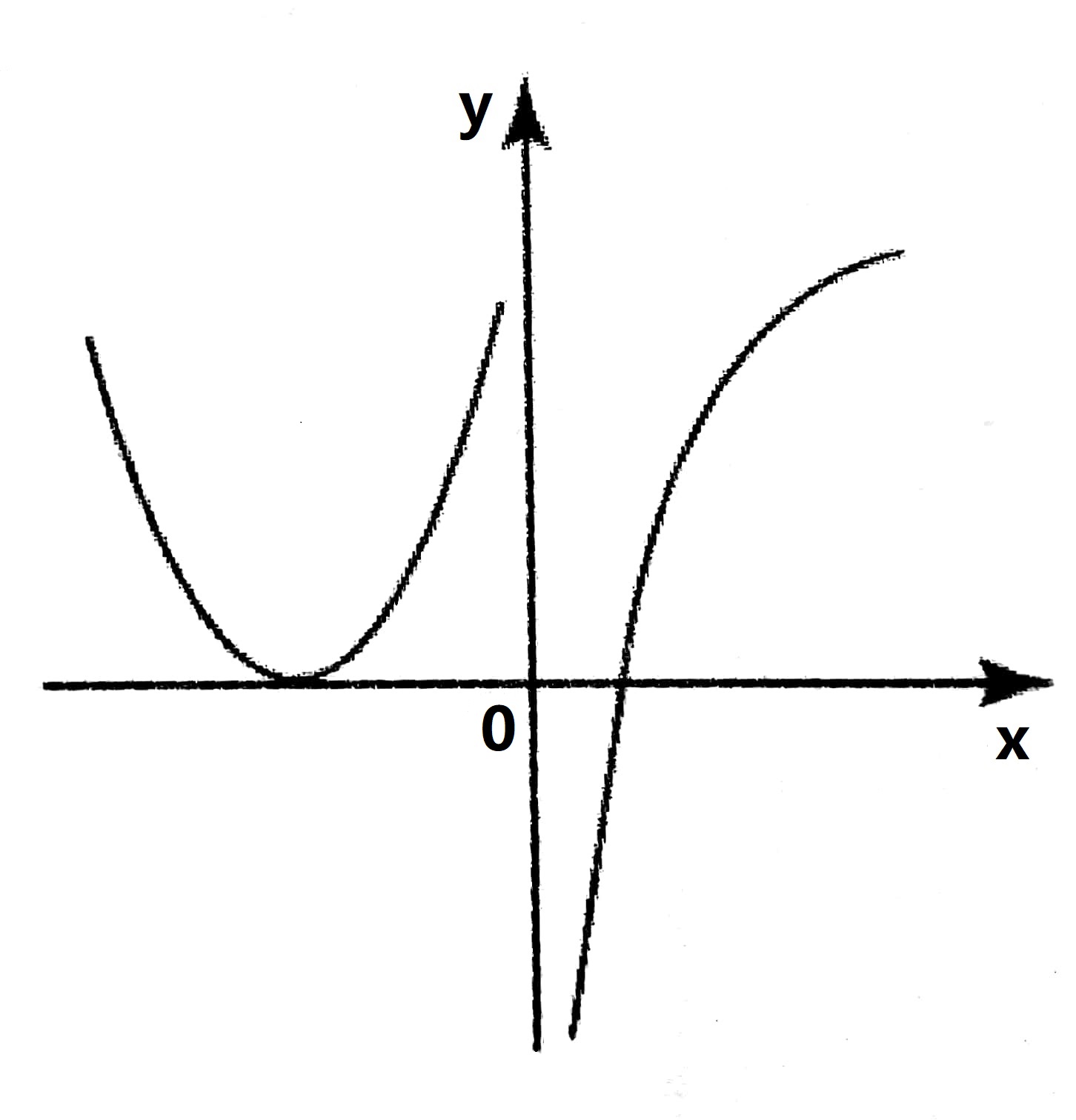
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续,其 $2$ 阶导函数 $f”(x)$ 的图形如图 1 所示,则曲线 $y$ $=$ $f(x)$ 的拐点的个数为 ( )
( A ) $0$.
( B ) $1$.
( C ) $2$.
( D ) $3$.
二、解析
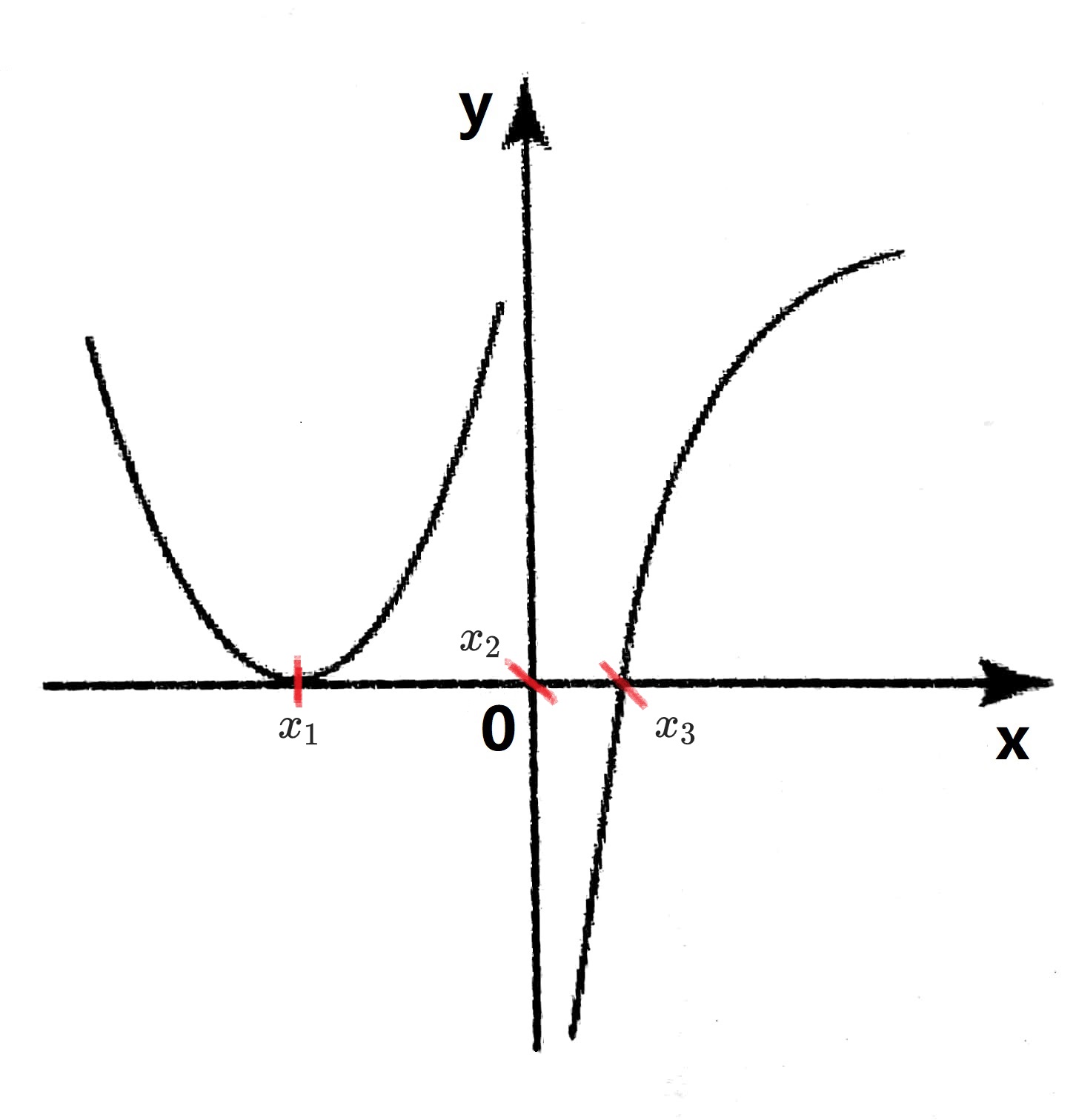
如图 2 所示,令左边的曲线与 $x$ 轴的交点为点 $x_{1}$, 坐标原点为点 $x_{2}$, 右边曲线与 $x$ 轴的交点为点 $x_{3}$:
由于本题涉及 2 阶导数,因此可以通过拐点存在的充分条件中的第一充分条件来判定:
若曲线 $y$ $=$ $f(x)$ 在 $x$ $=$ $x_{0}$ 处 $f”(x_{0})$ $=$ $0$ (或 $f”(x_{0})$ 不存在,但 $f(x)$ 在 $x$ $=$ $x_{0}$ 处连续),若 $f”(x)$ 在 $x_{0}$ 的左、右两侧邻域内异号,则 $(x_{0}$, $f(x_{0}))$ 为曲线 $y$ $=$ $f(x)$ 的拐点。
我们知道,对于连续函数的图像曲线而言,拐点处的图像曲线要么等于零,要么不存在。图 2 中的 $x_{1}$, $x_{2}$, $x_{3}$ ( $f”(x_{2})$ 虽然不存在,但是由题目中给出的“函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续”的条件我们知道,$f”(x_{2})$ 在点 $x_{2}$ 的左右两侧邻域是连续的,可能是原函数的一个拐点。)三个点均满足该条件。但是点 $x_{1}$ 两侧的函数都为正($f”(x)$ 的图像在 $x$ 轴上方),因此,不满足“左右两侧邻域内异号”的条件,因此,点 $x_{1}$ 不是函数 $f(x)$ 的拐点。点 $x_{2}$ 和 $x_{3}$ 两侧邻域的函数图像均异号,因此点 $x_{2}$ 和 $x_{3}$ 满足函数拐点存在的充分条件,函数 $f(x)$ 有两个拐点。
综上可知,本题的正确选项是:$C$.
EOF