一、题目
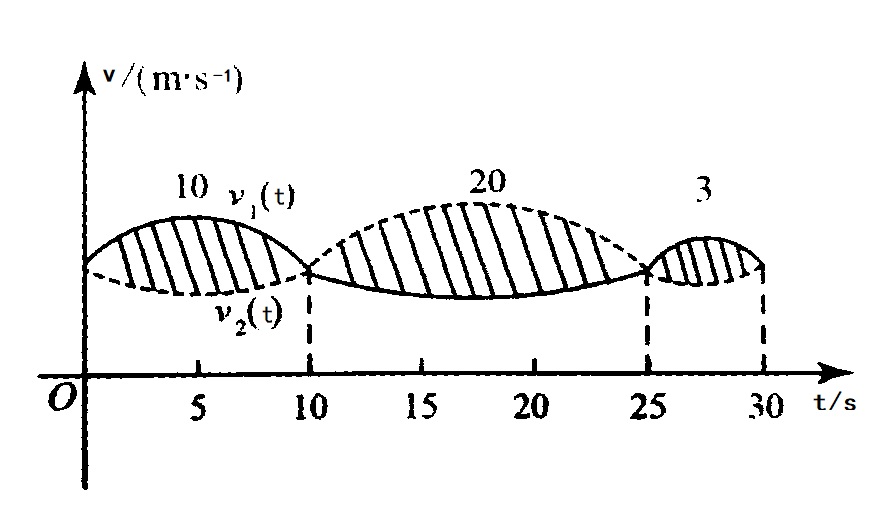
甲乙两人赛跑,计时开始时,甲在乙前方 $10$(单位:m)处. 图中,实线表示甲的速度曲线 $v$ $=$ $v_{1}(t)$ (单位 : m/s),虚线表示乙的速度曲线 $v$ $=$ $v_{2}(t)$ (单位 : m/s),三块阴影部分面积的数值依次为 $10$, $20$, $3$. 计时开始后乙追上甲的时刻记为 $t_{0}$ (单位 : s),则()
( A ) $t_{0}$ $=$ $10$.
( B ) $15$ $<$ $t_{0}$ $<$ $20$.
( C ) $t_{0}$ $=$ $25$.
( D ) $t_{0}$ $>$ $25$.
二、解析
方法一
从物理学的角度,本题就是考查速度与路程的关系。
题目中给出的 $X$ $-$ $Y$ 坐标图像是“时间-速度”图像。那么,根据物理学知识我们知道,该曲线与坐标轴围成的图像的面积就是走过的路程。我们又知道,实线表示甲,虚线表示乙,而且刚开始时甲在乙前面 $10$ 米处。
由图像可知,当 $t$ $=$ $10$ 时,甲在乙前面 $20$ 米处,当 $t$ $=$ $25$ 时,乙在第 $10$ 秒到第 $25$ 秒之间的 $15$ 秒时间里比甲多跑了 $20$ 米,正好抵消了之前乙落后于甲的 $20$ 米路程。因此,当 $t$ $=$ $25$ 时,乙追上了甲,即 $t_{0}$ $=$ $25$。
综上可知,本题的正确选项是:$C$.
方法二
从数学的角度,本题主要考查的是定积分的基本运算和定积分的几何意义。
使用高等数学解答本题需要如下关于定积分的知识:
- 定积分的几何意义:
曲边梯形的代数和. - 定积分的基本性质:
定积分的线性性:
$\int_{a}^{b}$ $[$ $k_{1}$ $f_{1}(x)$ $+$ $k_{2}$ $f_{2}(x)$ $]$ $dx$ $=$ $k_{1}$ $\int_{a}^{b}$ $f_{1}(x)$ $dx$ $+$ $k_{2}$ $\int_{a}^{b}$ $f_{2}(x)$ $dx$.
定积分积分区间的可加性:
$\int_{a}^{b}$ $f(x)$ $dx$ $=$ $\int_{a}^{c}$ $f(x)$ $dx$ $+$ $\int_{c}^{b}$ $f(x)$ $dx$.
根据上面的知识,我们可以做如下推理。
如果我们约定,使用 $v(t)$ 表示速度,使用 $s(t)$ 表示路程,那么在从 $0$ 到 $t$ 这个时间段内,可以写出如下定积分表达式:
$s(t)$ $=$ $\int_{0}^{t}$ $v(t)$ $dx$.
因此,当乙在 $t_{0}$ 时刻追上甲时,甲走过的路程为:
$s_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{1}(t)$.
乙走过的路程为:
$s_{2}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{2}(t)$.
$s_{2}(t)$
和 $s_{1}(t)$ 的关系为:
$s_{2}(t)$ $-$ $10$ $=$ $s_{1}(t)$.
于是有:
$s_{2}(t)$ $-$ $s_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{2}(t)$ $-$ $\int_{0}^{t_{0}}$ $v_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.
由于在从 $0$ 到 $10$ 秒的时间段内,$v_{2}$ 始终大于 $v_{1}$, 因此,乙超过甲的时间 $t_{0}$ 一定大于 $10$, 于是有:
$\int_{0}^{10}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $+$ $\int_{10}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.
又由于,从题中给出的图像我们可以看出:
$\int_{0}^{10}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.
因此有:
$\int_{10}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $20$. (1)
根据题中图像可知,在第 $10$ 秒到第 $25$ 秒这段时间里,图像中对应的阴影部分的面积为 $20$, 所以当 $t_{0}$ $=$ $25$ 时, $(1) $ 式成立。
综上可知,本题的正确选项是:$C$.
EOF