如果物理应用题没有配图，一定要注意判断自己画的图是否符合题意

一、题目

已知，无穷长直线 $L$ 的线密度为 $1$, 引力常数为 $k$, 则 $L$ 对距直线为 $a$ 的单位质点 $A$ 的引力是多少？

难度评级：

二、解析

首先，根据题目，我们可以绘制出如下示意图：

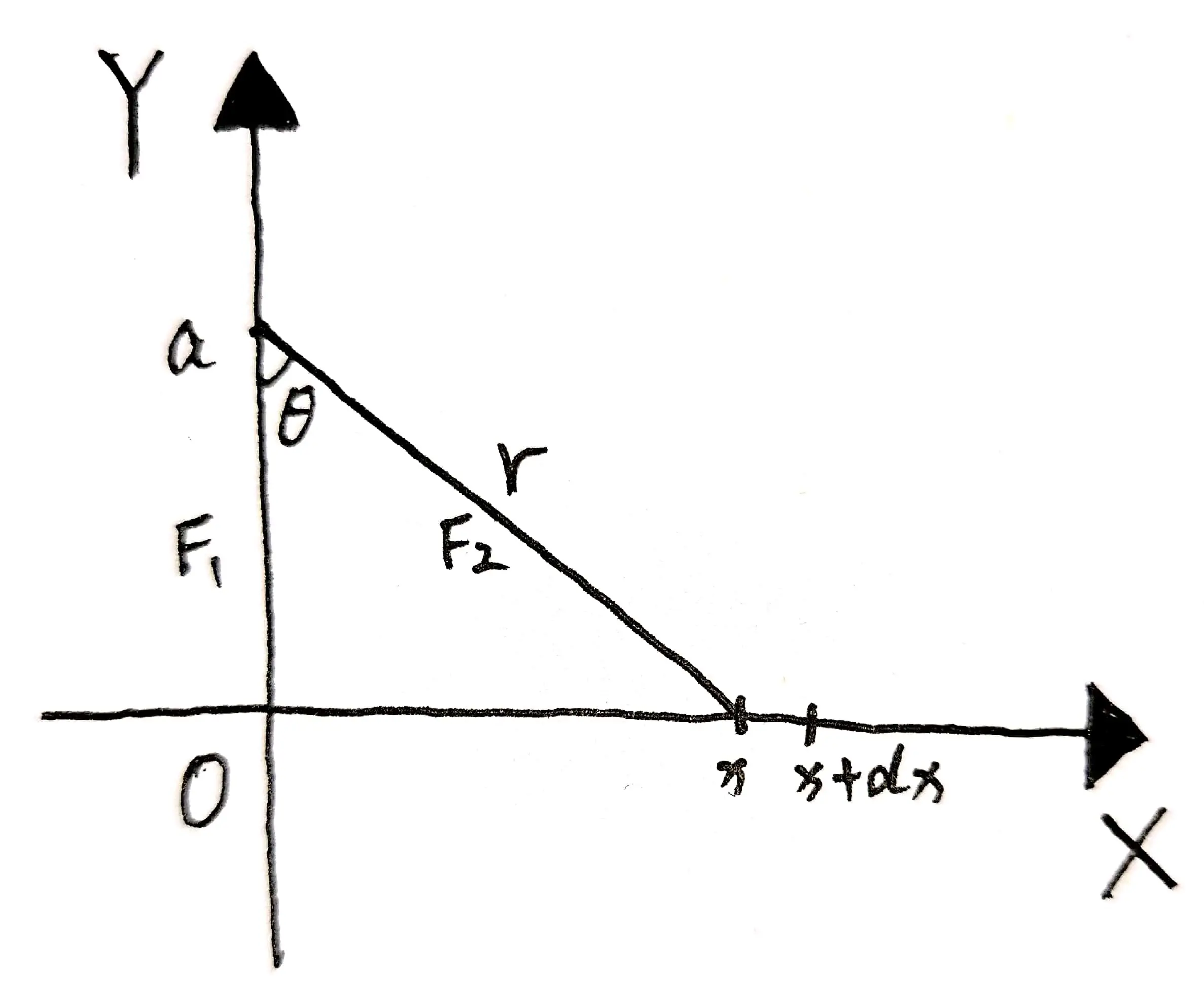
在上述示意图中，我们将 $X$ 轴作为直线 $L$, 而质点 A 则位于 $Y$ 轴上 $y=a$ 处。

观察可以发现，质点与直线上长度为 $\mathrm{d} x$ 的一个小段之间并不是垂直的，但是在研究力的作用时，我们必须把力分到 $X$ 轴和 $Y$ 上才可以进行积分运算，因此，我们设质点 A 与长度为 $\mathrm{d} x$ 的直线之间的力为 $F_{2}$, 该力在 $Y$ 轴上的分量为 $F_{1}$.

需要注意的是，本题与考研数学 1991 年的这道考研真题很相似，但也很不同。

$F_{2}$ 的表达式：

$$
F=G \frac{M m}{r^{2}} \Rightarrow F_{2}=k \frac{M \cdot 1}{r^{2}} \Rightarrow
$$

又：

$$
M=1 \cdot \mathrm{d} x
$$

于是：

$$
F_{2}=k \frac{\mathrm{d} x}{r^{2}} \Rightarrow
$$

$$
\mathrm{d} F_{2}=\frac{k \mathrm{~ d} x}{a^{2}+x^{2}}
$$

又：

$$
\frac{F_{1}}{F_{2}}=\cos \theta \Rightarrow F_{1}=F_{2} \cdot \cos \theta
$$

于是：

$$
\mathrm{d} F_{1} = \mathrm{d} F_{2} =\frac{k \mathrm{~ d} x}{a^{2}+x^{2}} \cdot \cos \theta
$$

又：

$$
\cos \theta=\frac{a}{\sqrt{a^{2}+x^{2}}}
$$

于是：

$$
\mathrm{d} F_{1}=\frac{k \mathrm{~ d} x}{a^{2}+x^{2}} \cdot \frac{a}{\sqrt{a^{2}+x^{2}}} \Rightarrow
$$

$$
\mathrm{d} F_{1}=\frac{a k \mathrm{~ d} x}{\left(a^{2}+x^{2}\right)^{\frac{3}{2}}} \Rightarrow
$$

由于 L 是无限长的，因此，要在 $(- \infty, + \infty)$ 上积分：

$$
F_{1}=\int_{-\infty}^{+\infty} \frac{a k \mathrm{~ d} x}{\left(a^{2}+x^{2}\right)^{\frac{3}{2}}}=
$$

$$
2 \int_{0}^{+\infty} \frac{a k \mathrm{~ d} x}{\left(a^{2}+x^{2}\right)^{\frac{3}{2}}}=
$$

$$
2 a k \int_{0}^{+\infty} \frac{1}{\left(a^{2}+x^{2}\right)^{\frac{3}{2}}} \mathrm{~ d} x \Rightarrow
$$

令（三角代换）：

$$
\textcolor{springgreen}{
x=\operatorname{atan} t \Rightarrow t \in\left(0, \frac{\pi}{2}\right) \Rightarrow
}
$$

$$
\textcolor{springgreen}{
a^{2}+x^{2}=a^{2}\left(1+\tan ^{2} t\right)=\frac{a^{2}}{\cos ^{2} t}
}
$$

$$
\textcolor{springgreen}{
\left(a^{2}+x^{2}\right)^{\frac{3}{2}}=\left(\frac{a^{2}}{\cos ^{2} t}\right)^{\frac{3}{2}}=\frac{a^{3}}{\cos ^{3} t}
}
$$

$$
\textcolor{springgreen}{
\mathrm{~ d} x=a \mathrm{~ d} (\tan t)=\frac{a}{\cos ^{2} t} \mathrm{~ d} t
}
$$

于是：

$$
2 a k \int_{0}^{+\infty} \frac{1}{\left(a^{2}+x^{2}\right)^{\frac{3}{2}}} \mathrm{~ d} x=2 a k \int_{0}^{\frac{\pi}{2}} \frac{\cos ^{3} t}{a^{3}} \cdot \frac{a}{\cos ^{2} t} \mathrm{~ d} t=
$$

$$
\frac{2 k}{a} \int_{0}^{\frac{\pi}{2}} \cos t \mathrm{~ d} t=\left.\frac{2 k}{a} \sin t\right|_{0} ^{\frac{\pi}{2}}=\frac{2 k}{a}
$$

---