题目
已知平面区域 $D =$ ${(x, y)|x^{2} + y^{2} \leqslant 2y }$, 计算二重积分 $\iint_{D} (x + 1)^{2} \mathrm{d} x \mathrm{d} y$.
解析
由题可知:
$$
x^{2} + y^{2} = 2y \Rightarrow
$$
$$
x^{2} + y^{2} – 2y = 0 \Rightarrow
$$
$$
{\color{Red}
x^{2} + (y – 1)^{2} = 1. \quad \quad {\color{White}①}
}
$$
由 $①$ 式可知,题目中所给的积分区域 $D$ 就是由一个圆心坐标 $O$ 为 $(0, 1)$, 半径 $r$ 为 $1$ 的圆形所围成的,且该圆形关于坐标轴的 $Y$ 轴对称,如图 01 所示:
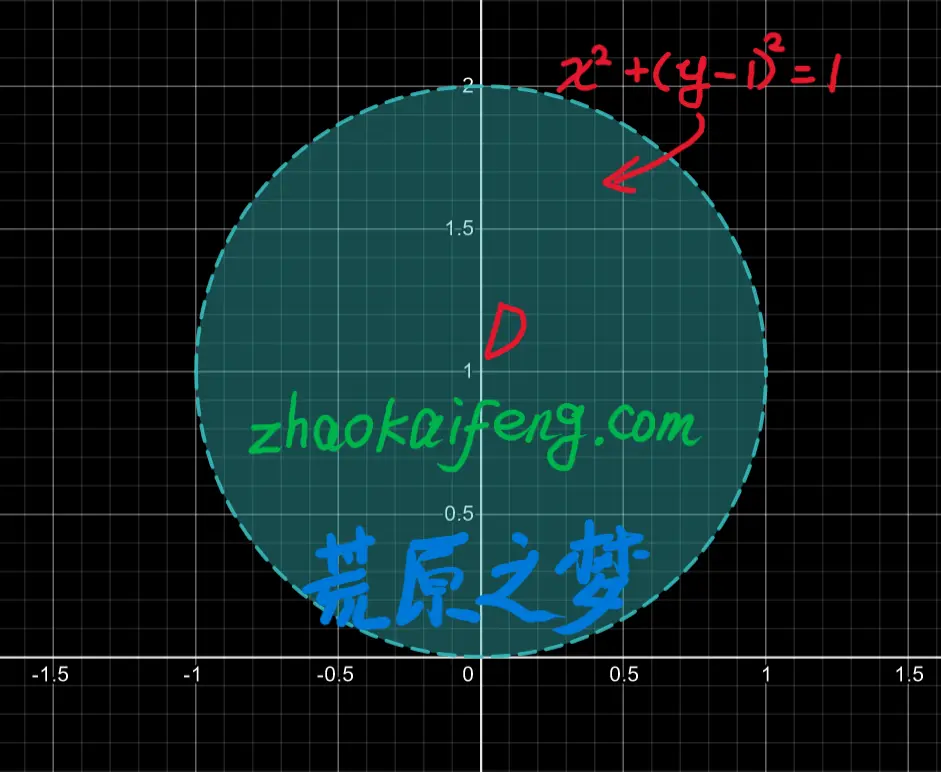
接着:
$$
\iint_{D} (x + 1)^{2} \mathrm{d} x \mathrm{d} y \Rightarrow
$$
$$
\iint_{D} (x ^{2} + 1 + 2x) \mathrm{d} x \mathrm{d} y \Rightarrow
$$
$$
\iint_{D} x ^{2} \mathrm{d} x \mathrm{d} y + \iint_{D} 1 \mathrm{d} x \mathrm{d} y + \iint_{D} 2x \mathrm{d} x \mathrm{d} y.
$$
由于 $2x$ 可被视为关于 $x$ 的奇函数,且积分区域 $D$ 关于坐标轴 $Y$ 轴对称,因此,根据二重积分的化简定律,可得:
$$
\iint_{D} 2x \mathrm{d} x \mathrm{d} y = 0.
$$
又:
$$
\iint_{D} 1 \mathrm{d} x \mathrm{d} y = \pi r^{2} = \pi.
$$
于是:
$$
\iint_{D} x ^{2} \mathrm{d} x \mathrm{d} y + \iint_{D} 1 \mathrm{d} x \mathrm{d} y + \iint_{D} 2x \mathrm{d} x \mathrm{d} y =
$$
$$
{\color{Red}
\iint_{D} x ^{2} \mathrm{d} x \mathrm{d} y + \pi. \quad \quad {\color{White}②}
}
$$
于是,我们接下来只需要求解出 $②$ 式中的 $\iint_{D} x ^{2} \mathrm{d} x \mathrm{d} y$, 即可求解完毕本题。
根据积分的特点,我们接下来需要将直角坐标系下的二重积分 $\iint_{D} x ^{2} \mathrm{d} x \mathrm{d} y$ 转换为极坐标系下的二重积分进行求解。
于是:
$$
\left\{\begin{matrix}
x = r \cos \theta;\\
y = r \sin \theta.
\end{matrix}\right.
\Rightarrow
$$
$$
x^{2} + y^{2} \leqslant 2y \Rightarrow
$$
$$
r^{2} \cos ^{2} \theta + r^{2} \sin ^{2} \theta \leqslant 2 r \sin \theta \Rightarrow
$$
$$
r^{2} (\cos ^{2} \theta + \sin ^{2} \theta) \leqslant 2 r \sin \theta \Rightarrow
$$
$$
r \leqslant 2 \sin \theta.
$$
接着:
$$
\iint_{D} x ^{2} \mathrm{d} x \mathrm{d} y \Rightarrow
$$
$$
\iint_{D} (r^{2} \cos ^{2} \theta) \cdot r \mathrm{d} r \mathrm{d} \theta \Rightarrow
$$
$$
\iint_{D} r^{3} \cos ^{2} \theta \mathrm{d} r \mathrm{d} \theta \Rightarrow
$$
$$
{\color{Red}
\int_{0}^{\pi} \mathrm{d} \theta \int_{0}^{2 \sin \theta} r^{3} \cos ^{2} \theta \mathrm{d} r}. \quad \quad {\color{White}③} \Rightarrow
$$
注:
[1]. 根据前面的图 01 可知,变量 $\theta$ 的取值范围是:$\theta \in (0, 2 \pi)$.
$$
\int_{0}^{\pi} \mathrm{d} \theta \cdot \Bigg[ \cos ^{2} \theta \int_{0}^{2 \sin \theta} r^{3} \mathrm{d} r \Bigg] \Rightarrow
$$
$$
\int_{0}^{\pi} \mathrm{d} \theta \cdot \Bigg[ \cos ^{2} \theta \cdot \frac{1}{4} r^{4} |_{0}^{2 \sin \theta} \Bigg] \Rightarrow
$$
$$
4 \int_{0}^{\pi} \cos ^{2} \theta \sin ^{4} \theta \mathrm{d} \theta \Rightarrow
$$
$$
2 \cdot 4 \int_{0}^{\frac{\pi}{2}} \cos ^{2} \theta \sin ^{4} \theta \mathrm{d} \theta \Rightarrow
$$
注:
[1]. 在区间 $(0, \pi)$ 上,$\cos^{2} \theta$ 和 $\sin ^{4} \theta$ 的图象都是关于 $x = \frac{\pi}{2}$ 对称的.
$$
8 \int_{0}^{\frac{\pi}{2}} (1 – \sin ^{2} \theta) \sin ^{4} \theta \mathrm{d} \theta \Rightarrow
$$
$$
8 \int_{0}^{\frac{\pi}{2}} (\sin ^{4} \theta – \sin ^{6} \theta) \mathrm{d} \theta \Rightarrow
$$
$$
8 \Bigg[\int_{0}^{\frac{\pi}{2}} \sin ^{4} \theta \mathrm{d} \theta – \int_{0}^{\frac{\pi}{2}} \sin ^{6} \theta \mathrm{d} \theta \Bigg] \Rightarrow
$$
$$
{\color{White}
华里士点火公式 \Rightarrow
}
$$
$$
8 (\frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2} – \frac{5}{6} \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}) \Rightarrow
$$
$$
8(\frac{3 \pi}{16} \cdot \frac{1}{6}) = \frac{\pi}{4}.
$$
于是,由 $②$ 式可知:
$$
\iint_{D} (x + 1)^{2} \mathrm{d} x \mathrm{d} y \Rightarrow
$$
$$
\iint_{D} x ^{2} \mathrm{d} x \mathrm{d} y + \pi \Rightarrow
$$
$$
\frac{\pi}{4} + \pi = \frac{5 \pi}{4}.
$$
