题目
编号:A2016218
设 $D$ 是由直线 $y = 1$, $y = x$, $y = – x$ 围成的有界区域,计算二重积分:
$$
\iint_{D} \frac{x^{2} – xy – y^{2}}{x^{2} + y^{2}}.
$$
解析
根据题目,我们可以画出如图 01 所示的积分区域 $D$ 的示意图:
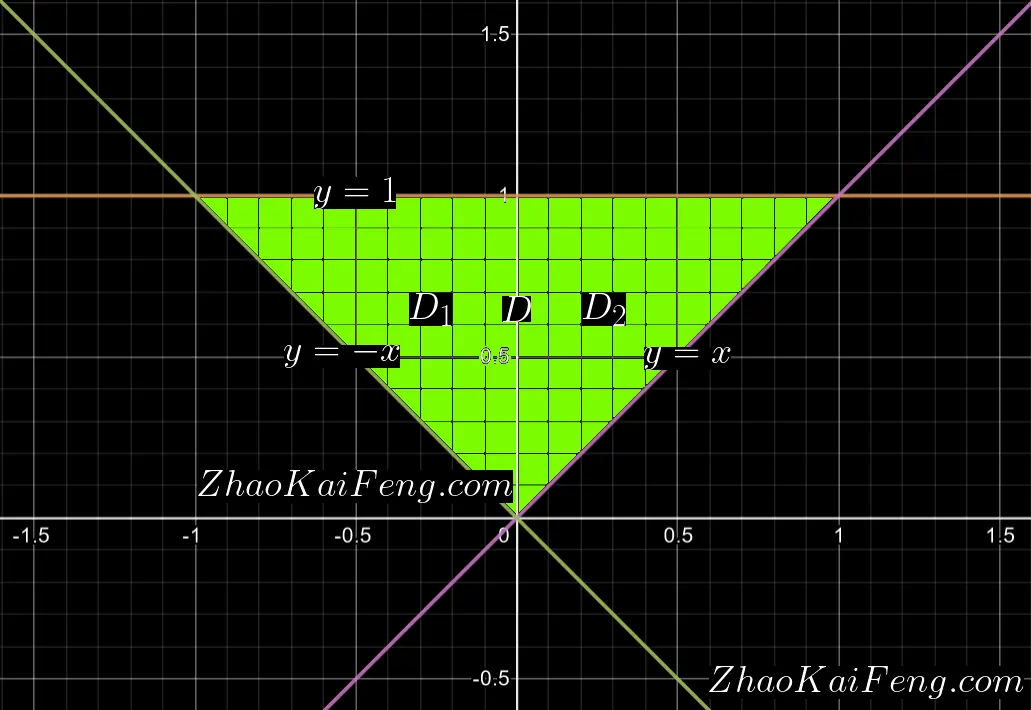
观察可知,积分区域 $D$ 由关于坐标轴 $Y$ 轴对称的两个区域 $D_{1}$ 和 $D_{2}$ 组成。于是,根据二重积分的化简定律,可知,关于 $x$ 是奇函数的式子 $xy$ 在关于 $Y$ 轴对称的积分区域 $D$ 上的积分一定为零:
$$
\iint_{D} xy = 0 \Rightarrow
$$
$$
\iint_{D} \frac{x^{2} – xy – y^{2}}{x^{2} + y^{2}} \rightrightarrows
$$
$$
\iint_{D} \frac{x^{2} – y^{2}}{x^{2} + y^{2}}. ②
$$
由于上面的 $②$ 式涉及到了 $x^{2}$, $y^{2}$ 以及 $x^{2} + y^{2}$, 因此,我们可以尝试将 $②$ 式转换成极坐标系下的二重积分进行计算。
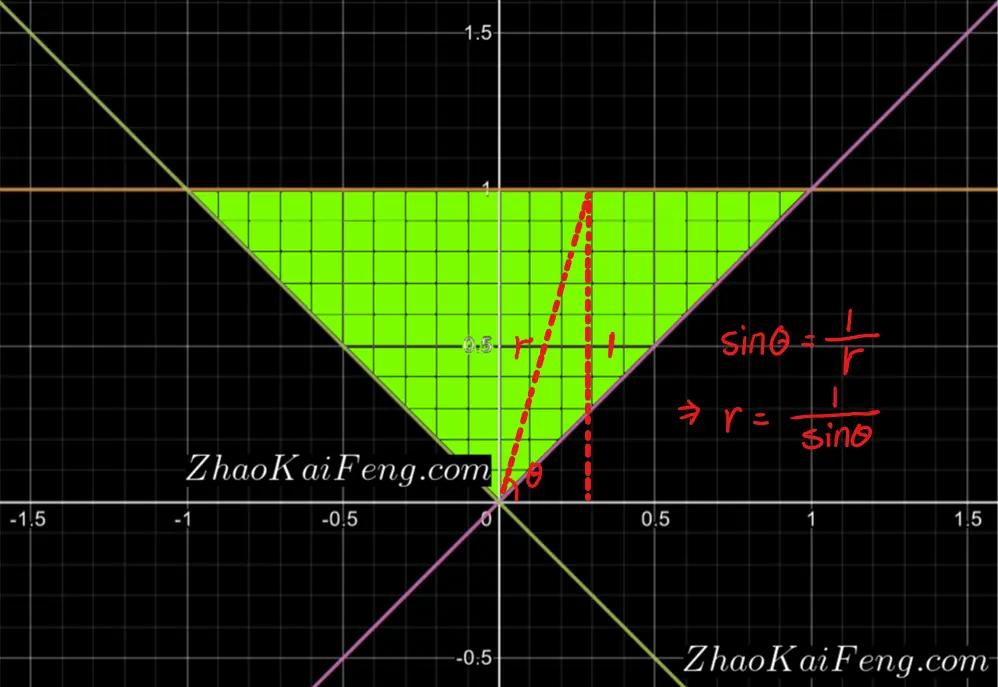
根据已知条件,以及上面图 02 的示意可知,在极坐标系下:
$$
\theta \in (45^{\circ}, 180^{\circ}-45^{\circ}) \Rightarrow
$$
$$
\theta \in (\frac{\pi}{4}, \frac{3 \pi}{4}).
$$
$$
\sin \theta = \frac{1}{r} \Rightarrow
$$
$$
r = \frac{1}{\sin \theta} \Rightarrow
$$
$$
r \in (0, \frac{1}{\sin \theta}).
$$
又:
$$
\left\{\begin{matrix}
x = r \cos \theta;\\
y = r \sin \theta.
\end{matrix}\right.
$$
于是:
$$
\iint_{D} \frac{x^{2} – y^{2}}{x^{2} + y^{2}} \Rightarrow
$$
$$
\iint_{D} \frac{r^{2} \cos ^{2} \theta – r^{2} \sin ^{2} \theta}{r^{2} \cos ^{2} \theta + r^{2} \sin ^{2} \theta} r \mathrm{d}r \mathrm{d} \theta \Rightarrow
$$
$$
\iint_{D} \frac{r^{2} (\cos ^{2} \theta – \sin ^{2} \theta)}{r^{2} (\cos ^{2} \theta + \sin ^{2} \theta)} r \mathrm{d}r \mathrm{d} \theta \Rightarrow
$$
$$
\iint_{D} \frac{(\cos ^{2} \theta – \sin ^{2} \theta)}{(\cos ^{2} \theta + \sin ^{2} \theta)} r \mathrm{d}r \mathrm{d} \theta \Rightarrow
$$
$$
\iint_{D} \frac{(\cos ^{2} \theta – \sin ^{2} \theta)}{1} r \mathrm{d}r \mathrm{d} \theta \Rightarrow
$$
$$
\iint_{D} r(\cos ^{2} \theta – \sin ^{2} \theta) \mathrm{d}r \mathrm{d} \theta \Rightarrow
$$
$$
\int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} (\cos ^{2} \theta – \sin ^{2} \theta) \mathrm{d} \theta \int_{0}^{\frac{1}{\sin \theta}} r \mathrm{d} r \Rightarrow
$$
$$
\int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} (\cos ^{2} \theta – \sin ^{2} \theta) (\frac{1}{2} r^{2}|_{0}^{\frac{1}{\sin \theta}}) \mathrm{d} \theta \Rightarrow
$$
$$
\int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} (\cos ^{2} \theta – \sin ^{2} \theta) (\frac{1}{2} \cdot \frac{1}{\sin ^{2} \theta}) \mathrm{d} \theta \Rightarrow
$$
$$
\frac{1}{2} \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} (\frac{\cos ^{2} \theta – \sin ^{2} \theta}{\sin ^{2} \theta}) \mathrm{d} \theta \Rightarrow
$$
$$
\frac{1}{2} \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} (\frac{\cos ^{2} \theta + \sin ^{2} \theta – 2 \sin ^{2} \theta}{\sin ^{2} \theta}) \mathrm{d} \theta \Rightarrow
$$
$$
\frac{1}{2} \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} (\frac{1}{\sin ^{2} \theta} – 2) \mathrm{d} \theta \Rightarrow
$$
$$
\frac{1}{2}[ \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} \frac{1}{\sin ^{2} \theta} \mathrm{d} \theta – \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} 2 \mathrm{d} \theta] \Rightarrow
$$
$$
\frac{1}{2}[ \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} \frac{1}{\sin ^{2} \theta} \mathrm{d} \theta – \pi] \Rightarrow
$$
$$
\frac{1}{2}[ \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} \csc ^{2} \theta \mathrm{d} \theta – \pi] \Rightarrow
$$
$$
\frac{1}{2}[ – \cot ^{2} \theta |_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} – \pi] \Rightarrow
$$
注:
[1]. $(\cot \theta)^{‘} =$ $-\csc ^{2} \theta$.
$$
\frac{1}{2}[\frac{-1}{\tan ^{2} \theta} |_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} – \pi] \Rightarrow
$$
注:
[1]. $\tan \frac{\pi}{4} = 1$;
[2]. $\tan \frac{3 \pi}{4} = – 1$.
$$
\frac{1}{2} [-1(-1-1) – \pi] = \frac{1}{2} [2- \pi] = 1 – \frac{\pi}{2}.
$$
