罗尔配拉格：罗尔定理是拉格朗日中值定理的前奏

一、题目

已知 $f(x)$ 在 $[a, b]$ 上连续，在 $(a, b)$ 二阶可导，且 $f(a)=f(b)$, $f^{\prime}(x)$ 在 $[a, b)$ 连续, $f_{+}^{\prime}(a)<0$, 则，是否 $\exists \ \xi \in(a, b)$, 使得 $f^{\prime \prime}(\xi)>0$ 成立？

难度评级：

二、解析

方法一：绘图法

我们可以根据题目信息，绘制出如下符合已知条件的函数图像，由于该函数是凹函数，因此，其二阶导函数一定大于零：

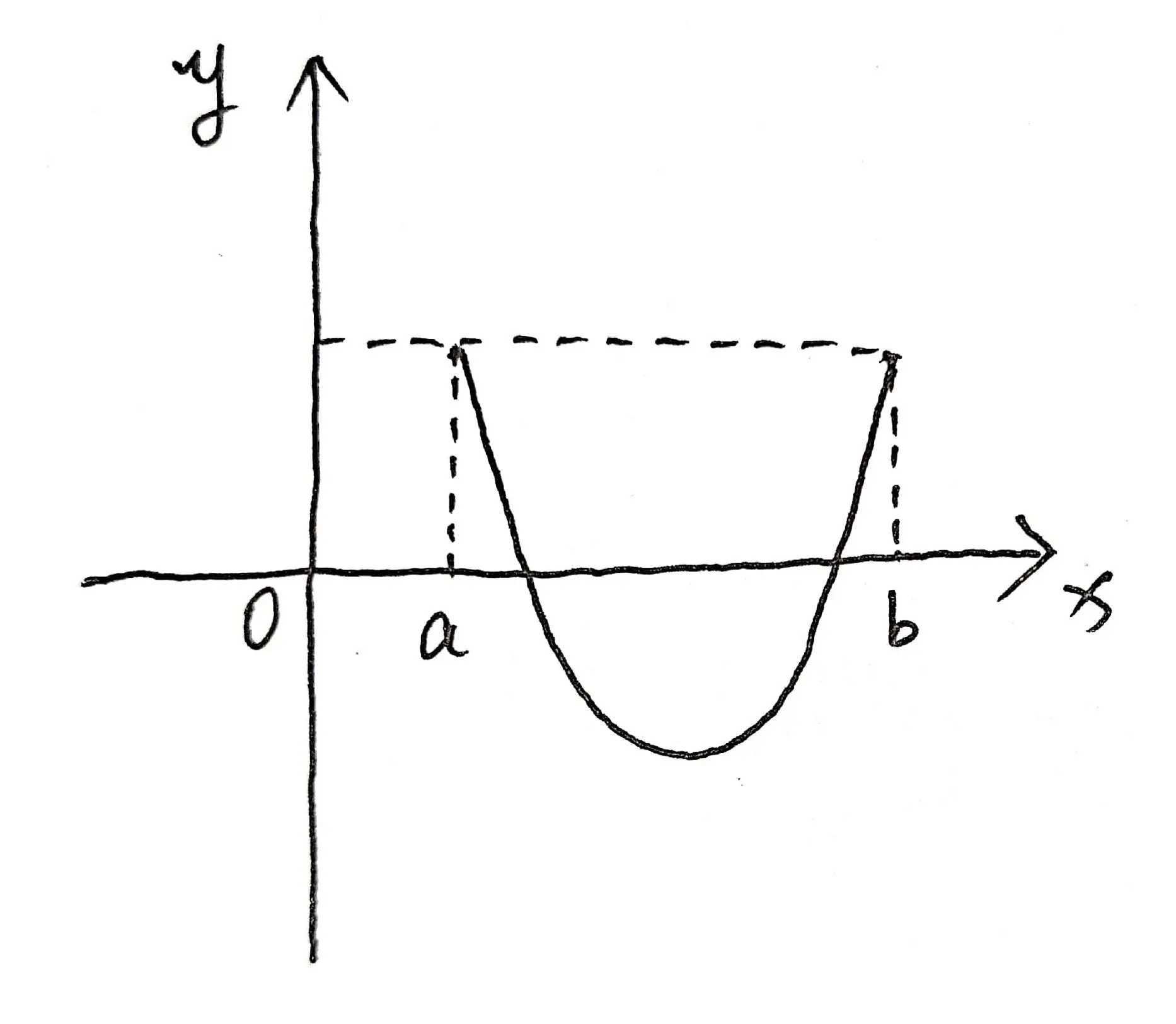
方法二：特例法

令：

$$
f(x)=-x(1-x), \ x \in[0,1]
$$

则：

$$
f^{\prime}(x)=-[(1-x)-x]=x-1+x=2 x-1
$$

满足：

$$
f_{+}^{\prime}(0)=-1<0
$$

且：

$$
f^{\prime \prime}(x)=2>0
$$

于是得证。

方法三：罗尔定理+拉格朗日中值定理

根据罗尔定理：

$$
\exists \ \eta \in(a, b) \Rightarrow f^{\prime}(\eta)=0
$$

于是，根据拉格朗日中值定理：

$$
\frac{f_{+}^{\prime}(a)-f^{\prime}(\eta)}{a-\eta}=f^{\prime \prime}(\xi), \quad \xi \in(a, \eta) \in(a, b)
$$

又：

$$
f_{+}^{\prime}(a)-f^{\prime}(\eta)=f_{+}^{\prime}(a)<0
$$

且：

$$
a < \eta \Rightarrow a-\eta<0
$$

因此：

$$
f^{\prime \prime}(\xi)>0, \ \xi \in(a, b)
$$

---