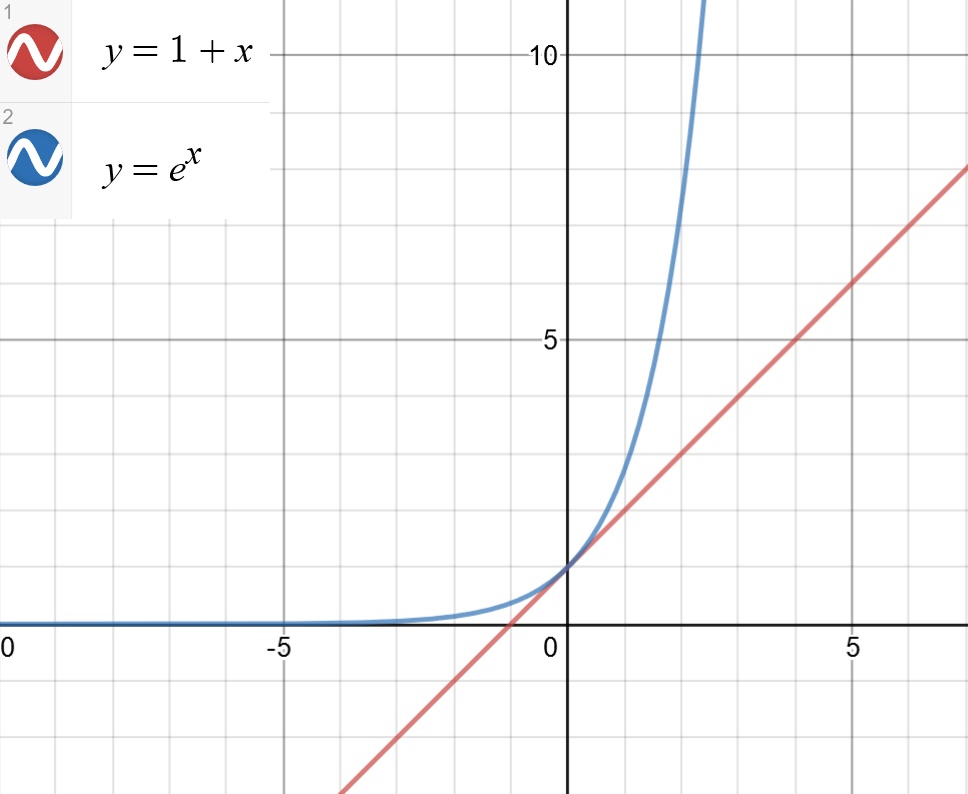标签： 高等数学练习题

一、题目

微分方程 $y”$ $+$ $2y’$ $+$ $3y$ $=$ $0$ 的通解为__.

二、解析

观察可知，这是一个二阶常系数线性齐次微分方程。

二阶常系数线性齐次微分方程的性质如下：

形如 $y”$ $+$ $py’$ $+$ $qy$ $=$ $0$, 其中 $p$, $q$ 均为常数。

特征方程为：$\lambda^{2}$ $+$ $p$ $\lambda$ $+$ $q$ $=$ $0$,

(1) 当 $\lambda_{1}$, $\lambda_{2}$ 为互异实根时，微分方程得通解为 $y(x)$ $=$ $C_{1}$ $e^{\lambda_{1}x}$ $+$ $C_{2}$ $e^{\lambda_{2}x}$;

(2) 当 $\lambda_{1}$ $=$ $\lambda_{2}$ 时，通解为 $y(x)$ $=$ $(C_{1}+C_{2}x)$ $e^{\lambda_{1}x}$;

(3) 当 $\lambda$ $=$ $\alpha$ $\pm$ $i$ $\beta$ （复数根）时，通解为 $y(x)$ $=$ $e^{\alpha x}$ $(C_{1}$ $\cos \beta$ $x$ $+$ $C_{2}$ $\sin \beta$ $x)$.

在本题中，特征方程中的 $p$ $=$ $2$, $q$ $=$ $3$, 因此特征方程为：

$\lambda^{2}$ $+$ $2$ $\lambda$ $+$ $3$ $=$ $0$. (1)

此外，我们还知道，对于形如 $a$ $x^{2}$ $+$ $bx$ $+$ $c$ $=0$ 的一元二次方程，其求根公式为：

$x$ $=$ $\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$.

于是，我们知道，对于 (1) 式：

$\lambda$ $=$ $\frac{-2\pm\sqrt{4-12}}{2}$ $=$ $\frac{-2\pm\sqrt{-8}}{2}$. (2)

我们又知道，在虚数中（复数包含虚数和实数），虚数单位 $i$ 有如下性质：

$i^{2}$ $=$ $-1$.

于是，(2) 式可以写成：

$\lambda$ $=$ $\frac{-2\pm\sqrt{8i^{2}}}{2}$ $=$ $\frac{-2\pm i 2 \sqrt{2}}{2}$ $=$ $-1$ $\pm$ $i$ $\sqrt{2}$.

于是，$\alpha$ $=$ $-1$, $\beta$ $=$ $\sqrt{2}$.

因此，正确答案是：

$y$ $=$ $e^{-x}$ $(C_{1}$ $\cos \sqrt{2}x$ $+$ $C_{2}$ $\sin \sqrt{2}$ $x$ $)$

EOF

一、题目

微分方程 $xy’$ $+$ $y$ $=0$ 满足条件 $y(1)$ $=$ $1$ 的解是 $y$ $=$__.

二、解析

由 $xy’$ $+$ $y$ $=0$ 得：

$(xy)’$ $=0$.

即：

$xy$ $=$ $C$ $\Rightarrow$ $y$ $=$ $\frac{C}{x}$

又因为 $y(1)$ $=$ $1$ $\Rightarrow$ $1$ $=$ $\frac{C}{1}$ $\Rightarrow$ $C$ $=$ $1$ $\Rightarrow$ $y$ $=$ $\frac{1}{x}$.

综上可知，正确答案是：$\frac{1}{x}$.

EOF

一、题目

设有两个数列 ${a_{n}}$, ${b_{n}}$, 若 $\lim_{n \rightarrow \infty}$ $a_{n}$ $=0$, 则（）

( A ) 当 $\sum_{n=1}^{\infty}$ $b_{n}$ 收敛时，$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ 收敛.

( B ) 当 $\sum_{n=1}^{\infty}$ $b_{n}$ 发散时，$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ 发散.

( C ) 当 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 收敛时，$\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ 收敛.

( D ) 当 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 发散时，$\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ 发散.

二、解析

由题目信息可知，当 $n$ $\rightarrow$ $\infty$ 时，数列 ${a_{n}}$ 是收敛的。

方法一：反例法

A 项：

令 $a_{n}$ $=$ $b_{n}$ $=$ $(-1)^{n-1}$ $\frac{1}{\sqrt{n}}$.

则此时 ${a_{n}}$ 是一个收敛数列，$\sum_{n=1}^{\infty}$ $b_{n}$ 也收敛（根据交错级数的莱布尼茨准则判别法可得此结论），但 $\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n}$ 发散（由常见级数的敛散性可得此结论）。

由此构成了对 A 项的反例，A 项错误。

注 1. 交错级数 $\sum_{n=1}^{\infty}$ $(-1)^{n-1}u_{n}$ $(u_{n}>0)$ 的判别法（莱布尼茨准则）：

若交错级数 $\sum_{n=1}^{\infty}$ $(-1)^{n-1}u_{n}$ $(u_{n}>0)$ 满足如下条件：

① $u_{n}$ $\geqslant$ $u_{n+1}$, $(n = 1,2,3, \dotsc)$;

② $\lim$ $u_{n}$ $=$ $0$,

则交错级数收敛，其和 $S$ $\leqslant$ $u_{1}$, 余项 $|R_{n}|$ $\leqslant$ $u_{n+1}$.

注 2. 常见级数的敛散性：

$p$ 级数 $\sum_{n=1}^{\infty}$ $\frac{1}{n^{p}}$ $\left\{\begin{matrix} 收敛 & p>1,\\ 发散 & p \leqslant 1. \end{matrix}\right.$

B 项：

令 $a_{n}$ $=$ $b_{n}$ $=$ $\frac{1}{n}$, 则

$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n^{2}}$.

此时，数列 ${a_{n}}$ 是一个收敛数列，$\sum_{n=1}^{\infty}$ $b_{n}$ 是发散的，但是 $\sum_{n=1}^{\infty}$ $\frac{1}{n^{2}}$ 是收敛的。

由此构成了对 B 项的反例，B 项错误。

D 项：

和 B 项一样，令 $a_{n}$ $=$ $b_{n}$ $=$ $\frac{1}{n}$, 则 $\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n^{4}}$ 是收敛的。

由此构成了对 D 项的反例，D 项错误。

综上可知，排除了 A, B, D 三个选项后，正确选项一定是 C 项。

方法二：用级数收敛的必要条件推导证明

我们可以使用级数收敛的必要条件直接证明 C 项正确。

级数 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛的必要条件：$\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$.

由于 $\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$ 是级数 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛的必要条件，因此，根据“小充分大必要”的原则，我们知道：

$\sum_{n=1}^{\infty}$ $u_{n}$ 收敛 $\Rightarrow$ $\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$;

$\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$ $\nRightarrow$ $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛。

由于 $\lim_{n \rightarrow \infty}$ $a_{n}$ $=$ $0$, 从而存在 $M$ $>$ $0$, 有 $|a_{n}|$ $\leqslant$ $M$, 即：

$a_{n}^{2}$ $b_{n}^{2}$ $\leqslant$ $M^{2}$ $b_{n}^{2}$. 又因为 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 收敛，故有：

$\lim_{n \rightarrow \infty}$ $|b_{n}|$ $=0$.

又根据如下定理：

设 $c$ 为非零常数，则 $\sum_{n=1}^{\infty}$ $u_{n}$ 与 $\sum_{n=1}^{\infty}$ $cu_{n}$ 具有相同的敛散性。

因此，$\sum_{n=1}^{\infty}$ $M^{2}$ $|b_{n}|$ 收敛，即：

$\lim_{n=1}^{\infty}$ $M^{2}$ $|b_{n}|$ $=$ $0$.

于是：

$\lim_{n \rightarrow \infty}$ $\frac{M^{2}|b_{n}||b_{n}|}{|b_{n}|}$ $=$ $\lim_{n \rightarrow \infty}$ $M^{2}$ $|b_{n}|$ $=$ $\lim_{n \rightarrow \infty}$ $\frac{M^{2}b_{n}^{2}}{|b_{n}|}$ $=$ $0$.

接下来，根据“比较判别法的极限形式”：

设 $\sum_{n=1}^{\infty}$ $u_{n}$ 与 $\sum_{n=1}^{\infty}$ $v_{n}$ 均为正项级数，且 $\lim_{n \rightarrow \infty}$ $\frac{u_{n}}{v_{n}}$ $=$ $A(v_{n} \neq 0)$.

① 若 $0$ $\leqslant$ $A$ $\leqslant$ $+$ $\infty$, 且 $\sum_{n=1}^{\infty}$ $v_{n}$ 收敛，则 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛.

② 若 $0$ $\leqslant$ $A$ $\leqslant$ $+$ $\infty$, 且 $\sum_{n=1}^{\infty}$ $v_{n}$ 发散，则 $\sum_{n=1}^{\infty}$ $u_{n}$ 发散.

于是我们知道，$\sum_{n=1}^{\infty}$ ${M^{2} b_{n}^{2}}$ 收敛。

又因为 $a^{2}$ $b^{2}$ $\leqslant$ $M^{2}$ $b^{2}$, 所以：

$\sum_{n=1}^{\infty}$ ${a^{2} b_{n}^{2}}$ 收敛.

由此得证 C 项正确。

EOF

一、题目

设 $M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{(1+x)^{2}}{1+x^{2}}$ $dx$, $N$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{1+x}{e^{x}}$ $dx$, $K$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $(1+\sqrt{\cos x})$ $dx$, 则 ( )

( A ) $M$ $>$ $N$ $>$ $K$

( B ) $M$ $>$ $K$ $>$ $N$

( C ) $K$ $>$ $M$ $>$ $N$

( D ) $K$ $>$ $N$ $>$ $M$

二、解析

在解答题目时，能化简的要先化简，能计算出具体数值的要先计算出具体数值。
首先观察本题，发现 $M$ 对应的式子应该是可以化简或者通过积分计算出具体的数值。于是：

$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{(1+x)^{2}}{1+x^{2}}$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{1+x^{2}+2x}{1+x^{2}}$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $[\frac{1+x^{2}}{1+x^{2}}$ $+$ $\frac{2x}{1+x^{2}}]$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $[$ $1$ $+$ $\frac{2x}{1+x^{2}}]$ $dx$

计算到上面这一步之后，我们有两种方法可以继续上面的计算，一种方法是利用积分函数在对称区间上的性质，另一种是利用基本积分公式直接计算。

下面分别使用上述提到的两种方法展开计算。

方法一：利用积分函数在对称区间上的性质

这里说的“对称区间”指的是关于原点对称的区间，观察题目可知，题目中的积分函数的上限和下限组成的区间 $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$ 正好是关于原点对称的。

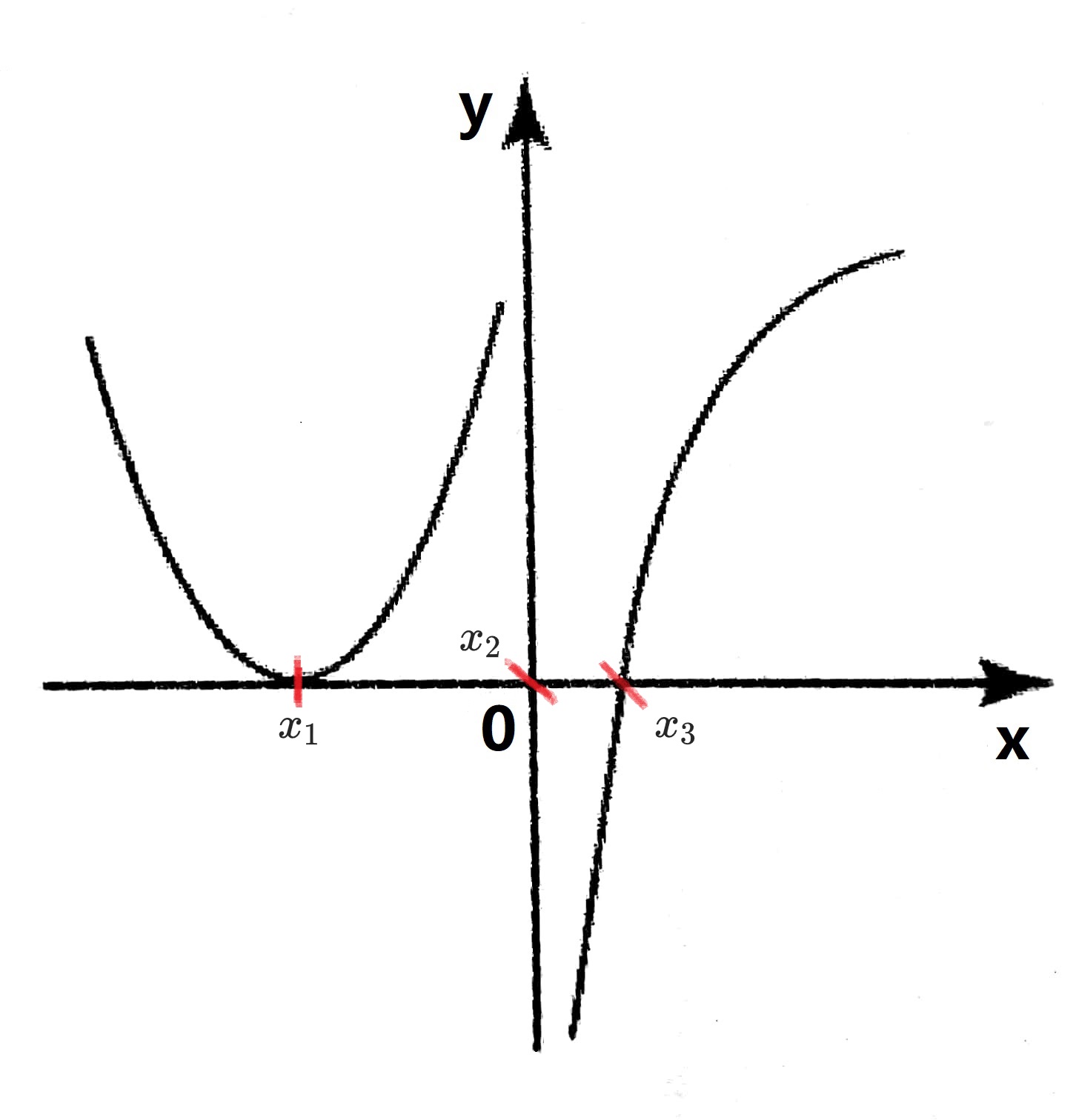
根据积分的几何意义，我们知道，奇函数在关于原点对称的对称区间上的积分是等于 $0$ 的。

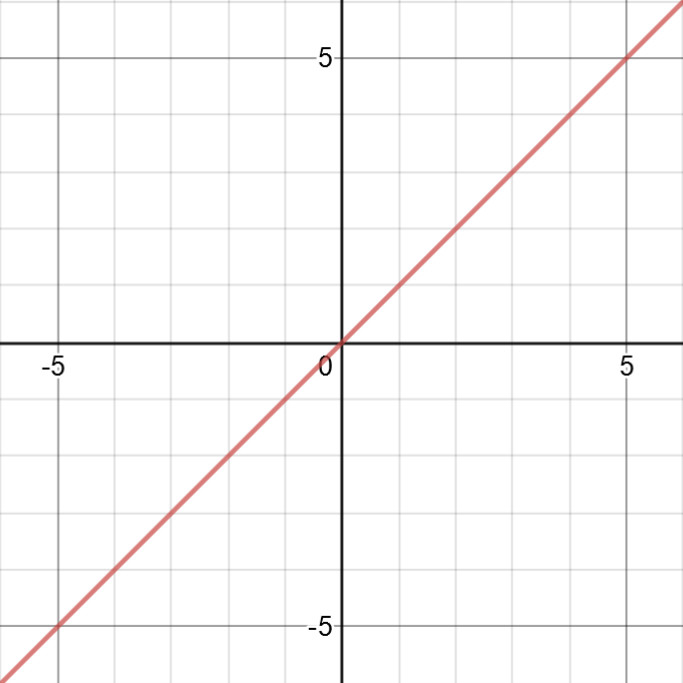
$y$ $=$ $x$, $x$ $\in$ $(-\infty,$ $+\infty)$ 就是一个典型的奇函数，如图 1：

因此，接下来，我们如果能证明一个函数是奇函数，就可以证明这个函数在关于原点对称的区间上的积分是 $0$.

于是，令：

$f(x)$ $=$ $\frac{2x}{1+x^{2}}$

则：

$\frac{2(-x)}{1+(-x)^{2}}$ $=$ $-\frac{2x}{1+x^{2}}$ $\Rightarrow$ $f(-x)$ $=$ $-f(x)$.

因此 $f(x)$ $=$ $\frac{2x}{1+x^{2}}$ 是一个奇函数，于是：

$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{2x}{1+x^{2}}$ $dx$ $=$ $0$.

即：

$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$.

方法二：利用基本积分公式直接计算

由前面的计算，我们已知，$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{2x}{1+x^{2}}$ $dx$, 于是，根据积分公式：

$d(x^{\mu})$ $=$ $\mu$ $x^{\mu-1}$ $dx$

我们可以令 $2x$ $dx$ $=$ $d(1+x^{2})$.

于是：

$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$ $+$ $\frac{d(1+x^{2})}{1+x^{2}}$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$ $+$ $\frac{1}{1+x^{2}}$ $d(1+x^{2})$.

接下来，根据基本积分公式：

$\int$ $\frac{1}{x}$ $dx$ $=$ $\ln |x|$ $+$ $c$.

我们有：

$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $+$ $\frac{1}{1+x^{2}}d(1+x^{2})$ $=$ $x$ $+$ $\ln |1+x^{2}|$ $+$ $c$ $|_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $=$ $\frac{\pi}{2}$ $+$ $|\ln[1+(\frac{\pi}{2})^{2}]|$ $+$ $c$ $-$ $(-\frac{\pi}{2})$ $-$ $|\ln[1+(-\frac{\pi}{2})^{2}]|$ $-$ $c$ $=$ $\frac{\pi}{2}+\frac{\pi}{2}$ $=$ $\pi$.

又因为，$M$ 的积分上限 $\frac{\pi}{2}$ 减去 $M$ 的积分下限 $-\frac{\pi}{2}$ 也等于 $\pi$.

根据定积分的基本性质：

$\int_{a}^{b}$ $1$ $dx$ $=$ $b$ $-$ $a$.

我们知道：

$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$.

补充：

如果是计算 $\int$ $\frac{2x}{1-x^{2}}$ $dx$, 则我们至少有以下两种计算方法：

$\int$ $\frac{2x}{1-x^{2}}$ $dx$ $=$ $-\int$ $\frac{1}{1-x^{2}}$ $=$ $-\ln |1-x^{2}|$ $+$ $c$;

或者：

$\int$ $\frac{2x}{1-x^{2}}$ $dx$ $=$ $\int$ $(\frac{1}{1-x}-\frac{1}{1+x})$ $dx$ $=$ $-\ln|x-1|$ $-$ $\ln|x+1|$ $+$ $c$ $=$ $-\ln|x^{2}-1|$ $+$ $c$.

至此，我们分别使用两种方法完成了对 $M$ 的化简计算。

根据定积分的比较定理：

设 $f(x)$ $\leqslant$ $g(x)$, $x$ $\in$ $[a,b]$, 则 $\int_{a}^{b}$ $f(x)$ $dx$ $\leqslant$ $\int_{a}^{b}$ $g(x)$ $dx$.

观察题目可知，题目中给出的三个定积分 $M$, $N$, $K$ 的上限和下限都是一样的，因此，我们可以使用上述比较定理比较他们的大小。

由于在 $M$, $N$, $K$ 中，我们目前已知的只有 $M$ 的数值，因此接下来我们先比较 $N$ 和 $K$ 中的积分函数与 $1$ 的大小关系。

首先来判断 $N$ 的积分函数和 $1$ 的大小关系。

当 $x$ $=$ $0$ 时，$1$ $+$ $x$ $=$ $e^{x}$ $=1$;

当 $x$ $<$ $0$ 时，$e^{x}$ 的减小速度小于 $1$ $+$ $x$ 的减小速度；

当 $x$ $>$ $0$ 时，$e^{x}$ 的增长速度大于 $1$ $+$ $x$ 的增长速度。

也就是说，在整个定义域内，$y$ $=$ $e^{x}$ 的函数图像始终在 $y$ $=$ $1$ $+$ $x$ 的上方或者和 $y$ $=$ $1$ $+$ $x$ 重合，他们二者的图像如图 2:

所以 $\frac{1+x}{e^{x}}$ $\leqslant$ $1$, $x$ $\in$ $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$. 再来判断 $K$ 的积分函数和 $1$ 的大小关系。

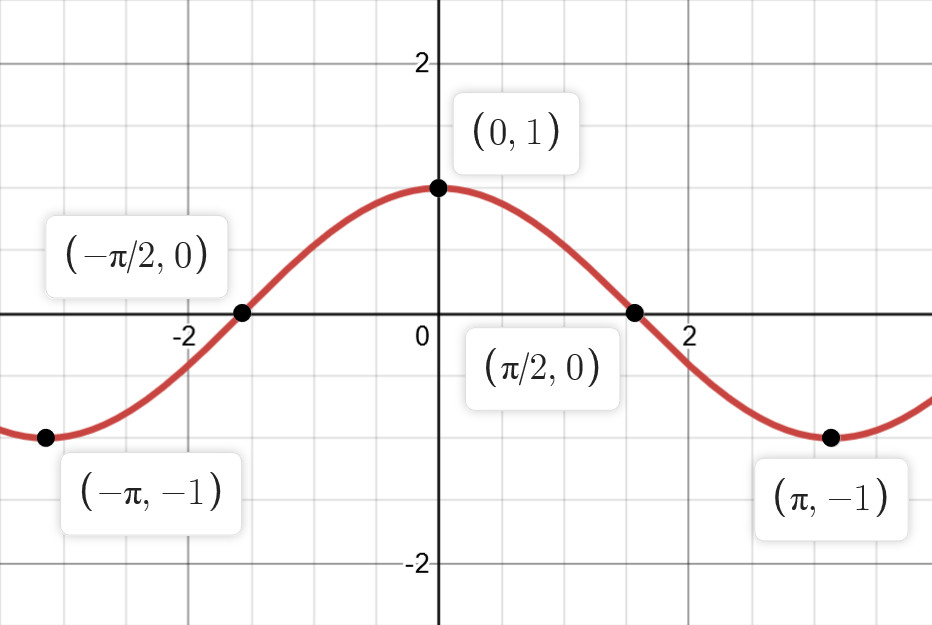
我们知道，当 $x$ $\in$ $[$ $-\frac{\pi}{2},$ $\frac{\pi}{2}$ $]$ 上时，$y$ $=$ $\cos x$ $\geqslant$ $0$ 的，如图 3:

于是 $1$ $+$ $\sqrt{\cos x}$ $\geqslant$ $1$.

综上可知：

$K$ $\geqslant$ $M$ $\geqslant$ $N$, 正确选项是：C

EOF

一、题目

设函数在 $f(x)$ 在 $(- \infty, + \infty)$ 内单调有界，${x_{n}}$ 为数列，下列命题正确的是 ( )

( A ) 若 ${x_{n}}$ 收敛，则 ${f(x_{n})}$ 收敛.

( B ) 若 ${x_{n}}$ 单调，则 ${f(x_{n})}$ 收敛.

( C ) 若 ${f(x_{n})}$ 收敛，则 ${x_{n}}$ 收敛.

( D ) 若 ${f(x_{n})}$ 单调，则 ${x_{n}}$ 收敛.

二、解析

解答本题之前，我们需要清楚“极限”，“收敛”和“有界”三者之间的区别与联系。

当我们说“极限”时，我们通常说的是“函数极限”，当我们说“收敛”时，我们通常说的是“数列收敛”。说“数列收敛”就是说该数列存在极限。我们可以认为，“收敛”是用于描述离散数据的，“极限”是用于描述连续数据的。当我们在计算或者证明数列极限的时候，我们其实是将数列看作了“连续数据”来对待。

如果一个数列收敛，那么这个数列必然有界，但是如果一个数列有界却不一定收敛，例如下面这个数列有界，但不收敛：

$\{1,-1,1,-1,1,-1\}$.

对于函数也一样，例如 $y$ $=$ $\sin x$ 是一个有界函数，但不收敛。

只有单调并且有界的数列才一定收敛（也意味着该数列一定有极限），这就是数列极限的“单调有界原理”。

注：当“单调有界原理”用在数列上时可以证明数列有界；当单调有界原理用在函数上时只能证明函数有确界，即有上确界或者下确界。

此外，本题还涉及复合函数，因此还必须清楚复合函数的几个性质：

• 复合函数的单调性

单调性包含单调递增和单调递减。对于复合函数而言，如果外函数和内函数都是单调函数，则在定义域内，它们的复合函数也是单调函数。至于是单调增还是单调减，可以用“同增异减”来判定。

“同增异减”的含义就是，如果外层函数是增函数，则复合函数的增减性与内函数的增减性一致；

如果外层函数为减函数，则复合函数的增减性与内函数的增减性相反。

“同增异减”也可以理解成，如果复合前两个函数都为增函数或者都为减函数，则复合函数为增函数；如果复合前两个函数一个为增函数，一个为减函数，则复合函数为减函数。

注：无论是单增还是单减，只要内函数和外函数都是单调函数，则复合函数也一定是单调函数。

• 复合函数的奇偶性

① 如果内函数为奇函数，则复合函数的奇偶性与外函数的奇偶性保持一致；

② 如果内函数为偶函数，则复合函数必为偶函数。

• 复合函数的周期性

① 若内函数为周期函数，则复合函数一定也是周期函数；

② 若外函数为周期函数，则复合函数不一定为周期函数。

• 复合函数的有界性

① 若内函数有界且外函数有界，则复合函数一定有界；

② 若内函数无界但外函数有界，则复合函数一定有界；

（上述两条总结一下就是，无论内函数是否有界，只要外函数有界，则复合函数一定有界。）

③ 若内函数有界但外函数无界或者内外函数都无界，这种情况下不能确定或者否定复合函数是有界还是无界，如果要确定或否定，还需要其他条件辅助分析。

有上面的阐述，我们可以发现，在判断复合函数的性质的时候，第一步要做的事情就是区分出内函数和外函数。本题在内外函数的区分上可能具有一定的迷惑性，我们不能认为在复合函数 “${f(x_{n})}$” 中，”${x_{n}}$” 是外函数而 “$f(x)$” 是内函数，这是错误的。符号 “${$” 和 “$}$” 只是说明这是一个数列，而并不是一个运算符号，其意义是多个 “$f(x_{n})$” 的值组成的数列，因此外函数是 “$f(x)$”, 内函数是 “$x_{n}$.”

下面是针对每个选项的具体分析：

A 项：

${x_{n}}$ 收敛 → ${x_{n}}$ 有界；

$f(x)$ 有界 + ${x_{n}}$ 有界 → ${f(x_{n})}$ 有界；

但是数列有界不能直接推出数列收敛，必须是单调且有界的数列才能推出收敛的结论。

A 项错误。

B 项：

${x_{n}}$ 单调 + $f(x_{n})$ 单调 → ${f(x_{n})}$ 单调；

$f(x_{n})$ 有界 → ${f(x_{n})}$ 有界；

${f(x_{n})}$单调有界 → ${f(x_{n})}$ 收敛。

B 项正确。

C 项：

由复合函数收敛不能确定其内函数是否也收敛。

C 项错误。

D 项：

$f(x_{n})$ 有界 → ${f(x_{n})}$ 有界；

${f(x_{n})}$单调有界 → ${f(x_{n})}$ 收敛；

但是 ${f(x_{n})}$ 收敛推不出内函数 ${x_{n}}$ 也收敛，和 C 项原因一致。

D 项错误。

综上可知，正确选项是：B

EOF

一、题目

$\sum_{n=0}^{\infty}(-1)^{n}$ $\frac{2n+3}{(2n+1)!}$ $=$__

( A ) $\sin$ $1$ $+$ $\cos 1$.

( B ) $2$ $\sin 1$ $+$ $\cos 1$.

( C ) $2$ $\sin 1$ $+$ $2$ $\cos 1$.

( D ) $2$ $\sin 1$ $+$ $3$ $\cos 1$.

二、解析

看到求和与阶乘，我们应该想到使用麦克劳林公式，因为麦克劳林公式中也包含求和运算与阶乘运算。因此，我们解答本题的入手点就是通过等价变形的方式把题目中的式子往常用的麦克劳林公式上凑。

$\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{2n+3}{(2n+1)!}$ $=$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{2n+1+2}{(2n+1)!}$ $=$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{2n+1}{(2n+1)!}$ $+$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{2}{(2n+1)!}$ $=$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{1}{(2n)!}$ $+$ $2$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{1}{(2n+1)!}$.

注意：上面式子中 “$\sum$” 符号前面的 “$2$” 特别容易在计算过程中丢掉，一定要记着带上！！！

我们知道在常用的五个函数的麦克劳林公式中，存在 “$(2n+1)!$” 和 “$(2n)!$” 是下面两个公式：

$\sin x$ $=$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{x^{2n+1}}{(2n+1)!}$, $x$ $\in R$;

$\cos x$ $=$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{x^{2n}}{(2n)!}$, $x$ $\in$ $R$.

当我们令 $x$ $=$ $1$ 时，就有：

$\sin x$ $=$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{1}{(2n+1)!}$

$\cos x$ $=$ $\sum_{n=0}^{\infty}$ $(-1)^{n}$ $\frac{1}{(2n)!}$

于是我们就有：

原式 $=$ $\cos 1$ $+$ $2$ $\sin 1$ $=$ $2$ $\sin 1$ $+$ $\cos 1$.

综上可知，正确选项是：D

EOF

一、题目

设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续，其 $2$ 阶导函数 $f”(x)$ 的图形如图 1 所示，则曲线 $y$ $=$ $f(x)$ 的拐点的个数为 ( )

( A ) $0$.

( B ) $1$.

( C ) $2$.

( D ) $3$.

二、解析

如图 2 所示，令左边的曲线与 $x$ 轴的交点为点 $x_{1}$, 坐标原点为点 $x_{2}$, 右边曲线与 $x$ 轴的交点为点 $x_{3}$:

由于本题涉及 2 阶导数，因此可以通过拐点存在的充分条件中的第一充分条件来判定：

若曲线 $y$ $=$ $f(x)$ 在 $x$ $=$ $x_{0}$ 处 $f”(x_{0})$ $=$ $0$ (或 $f”(x_{0})$ 不存在，但 $f(x)$ 在 $x$ $=$ $x_{0}$ 处连续)，若 $f”(x)$ 在 $x_{0}$ 的左、右两侧邻域内异号，则 $(x_{0}$, $f(x_{0}))$ 为曲线 $y$ $=$ $f(x)$ 的拐点。

我们知道，对于连续函数的图像曲线而言，拐点处的图像曲线要么等于零，要么不存在。图 2 中的 $x_{1}$, $x_{2}$, $x_{3}$ ( $f”(x_{2})$ 虽然不存在，但是由题目中给出的“函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续”的条件我们知道，$f”(x_{2})$ 在点 $x_{2}$ 的左右两侧邻域是连续的，可能是原函数的一个拐点。)三个点均满足该条件。但是点 $x_{1}$ 两侧的函数都为正($f”(x)$ 的图像在 $x$ 轴上方)，因此，不满足“左右两侧邻域内异号”的条件，因此，点 $x_{1}$ 不是函数 $f(x)$ 的拐点。点 $x_{2}$ 和 $x_{3}$ 两侧邻域的函数图像均异号，因此点 $x_{2}$ 和 $x_{3}$ 满足函数拐点存在的充分条件，函数 $f(x)$ 有两个拐点。

综上可知，本题的正确选项是：$C$.

EOF

一、题目

曲线 $y$ $=$ $(x-1)$ $(x-2)^{2}$ $(x-3)^{3}$ $(x-4)^{4}$ 的拐点是 ( )

( A ) $(1,0)$.

( B ) $(2,0)$.

( C ) $(3,0)$.

( D ) $(4,0)$.

二、解析

本题主要涉及求导，曲线的凹凸性，曲线凹凸性的判定，拐点的定义，拐点存在的充分条件这些知识。

曲线凹凸性的定义如下：

设函数 $f(x)$ 在区间 $I$ 上连续，若对 $I$ 上任意两点 $x_{1}$, $x_{2}$, 恒有：

$f(\frac{x_{1}+x_{2}}{2})$ $<$ $(>)$ $\frac{f(x_{1})+f(x_{2})}{2}$,

则称曲线 $y$ $=$ $f(x)$ 在区间 $I$ 上是向凹（凸）的.

曲线凹凸性的判定如下：

设函数 $f(x)$ 在 $[a,b]$ 上连续，在 $(a,b)$ 内具有二阶导数，那么：

① 如果在 $(a,b)$ 内 $f”(x)$ $>$ $0$, 则曲线 $y$ $=$ $f(x)$ 在 $[a,b]$ 上是凹的;

② 如果在 $(a,b)$ 内 $f”(x)$ $<$ $0$, 则曲线 $y$ $=$ $f(x)$ 在 $[a,b]$ 上是凸的.

拐点的定义如下：

设函数 $f(x)$ 在区间 $I$ 内连续，$x_{0}$ 是 $I$ 的内点，如果曲线 $y$ $=$ $f(x)$ 在经过点 $(x_{0},$ $f(x_{0}))$ 时凹凸性发生了改变，则称点 $(x_{0},$ $f(x_{0}))$ 为曲线的拐点.

拐点存在的充分条件如下：

第一充分条件：若曲线 $y$ $=$ $f(x)$ 在 $x$ $=$ $x_{0}$ 处 $f”(x_{0})$ $=0$ (或 $f”(x_{0})$ 不存在，但 $f(x)$ 在 $x$ $=$ $x_{0}$ 处连续)，若 $f”(x)$ 在 $x_{0}$ 的左右两侧邻域异号，则 $(x_{0},$ $f(x_{0}))$ 为曲线 $y$ $=$ $f(x)$的拐点.
第二充分条件：设 $f(x)$ 在 $x$ $=$ $x_{0}$ 的某邻域内有三阶导数，且 $f”(x_{0})$ $=$ $0$, $f”'(x_{0})$ $\neq$ $0$, 则 $(x_{0},$ $f(x_{0}))$ 为 $f(x)$ 的拐点.

回到本题。本题的原式是：

$y$ $=$ $(x-1)$ $(x-2)^{2}$ $(x-3)^{3}$ $(x-4)^{4}$.

观察可知，当 $x$ $=$ $1$, $2$, $3$, $4$ 时都可以使 $y$ $=$ $0$, 而我们在找拐点的时候，最重要的就是找到哪个点是大于零的，哪个点是小于零的或者哪个点是等于零的，上面式子的设定从计算上来看可以很快地找到这些特殊点。

求拐点的过程中少不了要计算导数，但是上面的式子太长，求导之后会更长，为了方便计算，尽可能避免出错，我们作如下约定：

令：

$A$ $=$ $(x-1)$;

$B$ $=$ $(x-2)^{2}$;

$C$ $=$ $(x-3)^{3}$;

$D$ $=$ $(x-4)^{4}$.

之后，我们有：

原式 $=$ $y$ $=$ $ABCD$.

于是我们有：

$y’$ $=$ $A’BCD$ $+$ $A(BCD)’$;

$y”$ $=$ $A”BCD$ $+$ $A'(BCD)’$ $+$ $A'(BCD)’$ $+$ $A(BCD)”$;

$y”’$ $=$ $A”’BCD$ $+$ $A”(BCD)’$ $+$ $A”(BCD)’$ $+$ $A'(BCD)”$ $+$ $A”(BCD)’$ $+$ $A’BCD”$ $+$ $A'(BCD)”$ $+$ $A(BCD)”’$;

令 $y’$ $=$ $0$, 则有：

$y'(2)$ $=$ $y'(3)$ $=$ $y'(4)$ $=$ $0$;

$y'(1)$ $\neq$ $0$. ($x$ $=$ $1$ 对应 $A$, 但是 $A’$ 是一个常数，不受 $x$ 的影响，因此 $x$ $=$ $1$ 不会使 $y’$ $=$ $0$, 以下计算过程中的判断与此类似.)

令 $y”$ $=$ $0$, 则有：

$y”(3)$ $=$ $y”(4)$ $=$ $0$;

$y”(1)$ $\neq$ $0$, $y”(2)$ $\neq$ $0$.

令 $y”’$ $=$ $0$, 则有：

$y”'(4)$ $=$ $0$;

$y”'(1)$ $\neq$ $0$, $y”'(2)$ $\neq$ $0$, $y”'(3)$ $\neq$ $0$.

通过上面的计算我们知道，$y”(3)$ $=$ $0$ 且 $y”'(3)$ $\neq$ $0$, 因此，根据拐点存在的充分条件中的第二充分条件，点 $(3,0)$ 是曲线 $y$ 的拐点。

综上可知，本题的正确选项是：C

EOF

一、题目

当 $x$ $\rightarrow$ $0$ 时，$f(x)$ $=$ $x$ $-$ $\sin ax$ 与 $g(x)$ $=$ $x^{2}$ $\ln(1-bx)$ 是等价无穷小，则（）

( A ) $a$ $=$ $1$, $b$ $=$ $-$ $\frac{1}{6}$.

( B ) $a$ $=$ $1$, $b$ $=$ $\frac{1}{6}$.

( C ) $a$ $=$ $-1$, $b$ $=$ $-\frac{1}{6}$.

( D ) $a$ $=$ $-1$, $b$ $=$ $\frac{1}{6}$.

二、解析

由于 $f(x)$ 和 $g(x)$ 是等价无穷小，因此，根据“无穷小的比较”中关于等价无穷小的定理：

设 $\lim$ $\alpha(x)$ $=$ $0$, $\lim$ $\beta(x)$ $=$ $0$,
若 $\lim$ $\frac{\alpha (x)}{\beta (x)}$ $=$ $1$, 则 $\alpha(x)$ 与 $\beta(x)$ 是等价无穷小，记为 $\alpha(x)$ $\sim \beta(x)$.

因此，我们有：

$\lim_{x \rightarrow 0}$ $\frac{f(x)}{g(x)}$ $=$ $\lim_{x\rightarrow 0}$ $\frac{x-\sin ax}{x^{2}\ln(1-bx)}$ $=$ $1$.

在“常用的等价无穷小”中，同时和 $\sin x$ 与 $x$ 有关的等价无穷小两个，如下：

$\sin x$ $\sim x$;

$x$ $-$ $\sin x$ $\sim$ $\frac{1}{6}x^{3}$.

同时和 $\ln x$ 与 $x$ 有关的等价无穷小也有两个，如下：

$\ln(1+x)$ $\sim x$;

$x$ $-$ $\ln(1+x)$ $\sim$ $\frac{1}{2}x^{2}$.

那么，我们现在需要考虑的问题就是：需要组合使用哪两个等价无穷小化简原式？

这里选择并确定使用哪两个等价无穷小的依据就是题目中给出的“等价无穷小”。也就是说，在对原式进行化简运算的过程中，必须保证分子分母互为等价无穷小，每一步都要遵守这个原则，最后化简出来的结果中分子分母也必须互为等价无穷小，只有这样才可以和原式划等号。

由前面的计算我们知道，原式的分子是：

$x$ $-$ $\sin ax$

原式的分母是：

$x^{2}$ $\ln(1-bx)$

于是，分子的有效化简形式有以下四种：

$x$ $-$ $\sin ax$ $=$ $x$ $-$ $ax$ (1)

或者：

$x$ $-$ $\sin ax$ $=$ $\sin x$ $-$ $\sin ax$ (2)

或者：

$x$ $-$ $\sin ax$ $=$ $x$ $-$ $[ax$ $-$ $\frac{1}{6}$ $(ax)^{3}]$ $=$ $x$ $-$ $ax$ $+$ $\frac{1}{6}$ $a^{3}$ $x^{3}$ (3)

或者：

$x$ $-$ $\sin ax$ $=$ $\frac{1}{6}x^{3}$ $+$ $\sin x$ $-$ $\sin ax$ (4)

分母的有效化简形式有以下两种：

$x^{2}$ $\ln(1-bx)$ $=$ $x^{2}$ $(-bx)$ $=$ $-bx^{3}$ (5)

或者：

$x^{2}$ $\ln(1-bx)$ $=$ $x^{2}$ $[(-bx)$ $-$ $\frac{1}{2}$ $(-bx)^{2}]$ $=$ $-bx^{3}$ $-$ $\frac{1}{2}$ $b^{2}$ $x^{4}$ (6)

由于要保证每一步计算过程中分子分母都是等价无穷小，因此，我们首先要看看那些式子组合起来可以形成等价无穷小。

(1) 到 (6) 六个式子中变量 $x$ 的次方数情况如下：

(1): 只包含 $1$ 次方；

(2): 只包含 $1$ 次方；

(3): 包含 $1$ 次方和 $3$ 次方；

(4): 包含 $1$ 次方和 $3$ 次方；

(5): 只包含 $3$ 次方；

(6): 包含 $3$ 次方和 $4$ 次方。

由于分母对应的 (5) 和 (6) 两个式子都包含 $3$ 次方，分子对应的 (1) 式和 (2) 式无论如何变化也不会出现 $3$ 次方，无法与分母构成等价无穷小，因此排除。此外，(4) 式有 $\sin x$ 和 $\sin ax$, 而分母中并没有对应的形式，因此 (4) 式被基本排除。

现在就剩下分子对应的 (3) 式和分母对应的 (5) 式和 (6) 式了。由于 (6) 式中含有 $x$ 的 4 次方，而 (3) 式无论如何变化也不会出现 4 次方，因此，正确的化简过程应该在 (3) 式和 (5) 式中产生。

基于以上分析，尝试化简如下：

原式 $=$ $\lim_{x\rightarrow 0}$ $\frac{x-ax+\frac{1}{6}a^{3}x^{3}}{-bx^{3}}$ $=$ $\lim_{x\rightarrow0}$ $\frac{(1-a)x+\frac{1}{6}a^{3}x^{3}}{-bx^{3}}$

分母中没有 $1$ 次方，因此，为了保证“分子分母互为等价无穷小”这个条件始终成立，唯一的办法就是令 $1$ $-$ $a$ $=0$, 接下来，根据 $f(x)$ $\sim$ $g(x)$ 所得的分子分母的对应关系，我们可以得到：

$\frac{1}{6}a^{3}$ $=$ $-b$

两式联立：

$\left\{\begin{matrix}1-a=0,\\ \frac{1}{6}a^{3}=-b.\end{matrix}\right.$

解得：

$\left\{\begin{matrix} a=1,\\ b=-\frac{1}{6}.\end{matrix}\right.$

综上可知，本题的正确选项是：$A$

通过本题，我们可以总结出使用等价无穷小化简原式过程中的以下规律：

• 注意原式分子分母的无穷小类型（等价，高阶，低阶，同阶，$K$ 阶），计算过程中要以始终保持一致的无穷小类型为所有计算的前提；
• 使用常见等价无穷小化简的时候一般都是由繁化简，即化简的趋势都是使式子中尽可能只出现 $x$, 例如将 $\sin x$ 化为 $x$, 将 $\ln(1+x)$ 化为 $x$ 等。
• 此外，把式子中的一部分化为和另一部分相同类型的形式更有可能简化运算，例如在本题中，分母是 $x^{2}$ $\ln(1-bx)$, 则把 $\ln(1-bx)$ 化为 $-bx$ 显然会让式子在形式上更统一，更有利于后面的计算；
• 化简过程要严格按照公式进行，特别要注意负号和变量前面的参数，必要时要先加上括号维持原来的形式，之后一步步计算。

一、题目

曲线 $\sin (xy)$ $+$ $\ln(y-x)$ $=x$ 在点 $(0,1)$ 处的切线方程为__.

本题需要用到求导法则和切线方程公式的相关知识。

需要用到的求导公式有：

$(\sin x)’$ $=$ $\cos x$;

$(\ln x)’$ $=$ $\frac{1}{x}$;

$(ab)’$ $=$ $a’b$ $+$ $ab’$;

$f'(x)$ $=$ $f'[\phi(x)]$ $\cdot$ $\phi'(x)$.

求导过程中另外需要注意的两点如下：

• 对 $x$ 求导，则包括 $x$ 和其他常量都要按照求导公式进行计算，而除了 $x$ 之外的其他变量则只加上求导符号 (例如: $’$) 即可，不进行求导计算；
• 等式两边对同一变量求导后，等式仍然成立。因为求导前是等式，求导规则也一致，则求导后等式两边仍然恒等。

切线方程的计算公式如下：

$y$ $-$ $f(x_{0})$ $=$ $f'(x_{0})$ $(x-x_{0})$.

解答思路如下：

由于切线方程的计算公式中包含导数 $f'(x)$，因此，首先需要计算出导数。原式两边同时对 $x$ 求导可以产生导数 $y’$：

$[\sin(xy)$ $+$ $\ln(y-x)]’$ $=$ $(x)’$ $\Rightarrow$ $\cos(xy)$ $(x’y+xy’)$ $+$ $\frac{1}{y-x}$ $(y-x)’$ $=$ $1$ $\Rightarrow$ $\cos(xy)$ $(y$ $+$ $xy’$ $)$ $+$ $\frac{1}{y-x}$ $(y’$ $-$ $1$ $)$ $=$ $1$.

要求的是曲线在点 $(0,1)$ 处的切线方程，因此，我们把 $x$ $=$ $0$; $y$ $=$ $1$带入上面的到的式子中，得：

$1$ $\cdot$ $1$ $+$ $1$ $\cdot$ $(y’$ $-$ $1$ $)$ $=$ $1$ $\Rightarrow$ $1$ $+$ $y’$ $-$ $1$ $=$ $1$ $\Rightarrow$ $y’$ $=$ $1$.

即：

$y'(0)$ $=$ $1$.

将上述结果带入切线方程求导公式得：

$y$ $-$ $1$ $=$ $1$ $\cdot$ $($ $x$ $-$ $0$ $)$ $\Rightarrow$ $y$ $=$ $x$ $+$ $1$.

综上可知，本题得答案是：$y$ $=$ $x$ $+$ $1$.

EOF

一、题目

设函数 $f(x)$ $=$ $\int_{0}^{x^{2}}$ $\ln(2+t)$ $dt$, 则 $f'(x)$ 的零点个数（）

( A ) $0$.

( B ) $1$.

( C ) $2$.

( D ) $3$.

二、解析

本题可以使用积分和导数的相关定理解出。

涉及到的积分知识如下：

(1) 定积分基本性质

$\int_{a}^{b}$ $f(x)$ $dx$ $=$ $\int_{a}^{b}$ $f(t)dt$;

(2) 变上限积分函数求导

• 若 $f(x)$ 在 $[a,b]$ 上连续，则 $F(x)$ $=$ $\int_{a}^{x}$ $f(t)$ $dt$ 在 $[a,b]$ 上可导，且 $F'(x)$ $=$ $f(x)$.
• 若 $f(x)$ 在 $[a,b]$ 上连续，$\phi(x)$ 在 $[a,b]$ 上可导，设$F(x)$ $=$ $\int_{a}^{\phi(x)}$ $f(t)$ $dt$, 则：

$F'(x)$ $=$ $f[\phi(x)]$ $\cdot$ $\phi'(x)$.

涉及到的求导知识如下：

$(x^{a})’$ $=$ $ax^{a-1}$;

此外，我们需要知道的是，“函数零点”指的是 $f(x)$ $=$ $0$ 时，对应的自变量 $x$ 的数值，“函数零点” 不是一个点，而是一个数值。

解题思路如下：

根据变上限积分函数求导法则，有：

$f'(x)$ $=$ $\ln(2+x^{2})$ $\cdot$ $(x^{2})’$ $=$ $2$ $x$ $\ln(2+x^{2})$.

则要求函数 $f'(x)$ 的零点的个数，就是求 $2$ $x$ $\ln(2+x^{2})$ $=$ $0$ 的解的个数。

要使 $2$ $x$ $\ln(2+x^{2})$ $=$ $0$ 成立，则有以下三种情况（分情况讨论时要注意“不重不漏”）：

(1) $2$ $x$ $=$ $0$ 且 $\ln(2+x^{2})$ $\neq$ $0$

此时解出 $x$ $=$ $0$.

(2) $2$ $x$ $\neq$ $0$ 且 $\ln(2+x^{2})$ $=$ $0$.

无解。

由于 $1$ $+$ $x^{2}$ $\geq$ $2$ 始终成立，而且当 $x$ $=$ $1$ 时，$\ln(x)$ $=$ $0$, 当 $x$ $>$ $1$ 时，$\ln(x)$ $>$ $0$.

所以，$\ln(2+x^{2})$ $>$ $0$ 始终成立，与 $x$ 轴没有交点。

(3) $2$ $x$ $=$ $0$ 且 $\ln(2+x^{2})$ $=$ $0$

$2$ $x$ $=$ $\ln(2+x^{2})$ $=$ $0$ $\Rightarrow$ 无解.

综上可知，当 $2$ $x$ $\ln(2+x^{2})$ $=$ $0$ 时，有：

$x$ $=$ $0$.

因此，只有一个零点，答案是：$B$.

EOF

一、题目

求极限 $\lim_{x \rightarrow 0}$ $\frac{[\sin x-\sin (\sin x)] \sin x}{x^{4}}$

二、解析

当题目中要求的是“极限”，而且出现了 $x$ $\rightarrow$ $0$ 时就要考虑是不是要用到或者可以用到等价无穷小。

还需要考虑的可能用到的知识是洛必达法则。当 $x$ $\rightarrow$ $0$ 时可能产生 $\frac{0}{0}$ 型的洛必达或者 $\frac{\infty}{\infty}$ 型的洛必达。而且，洛必达法则就是为求极限而生的，可以把对函数的求极限转换成对函数的导数求极限，从而可能化简原式。

方法一

本题考查的是等价无穷小，需要用到的两个等价无穷小如下（当 $x$ $\rightarrow$ $0$ 时）：

$x$ $\sim$ $\sin x$;

$x$ $-$ $\sin x$ $\sim$ $\frac{1}{6}x^{3}$.

于是有：

原式 $=$ $\lim_{x \rightarrow 0}$ $\frac{[\sin x-\sin (\sin x)]\sin x}{\sin^{4}x}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{\sin x-\sin(\sin x)}{\sin^{3} x}$

令 $\sin x$ $=$ $t$, 则有：

原式 $=$ $\lim_{x \rightarrow 0}$ $\frac{t-\sin(t)}{t^{3}}$

由于，当 $x$ $\rightarrow$ $0$ 时，$\sin x$ $\rightarrow$ $0$, 于是有 $t$ $\rightarrow$ $0$, 因此根据常见的等价无穷小，有：

$t$ $-$ $\sin t$ $\sim$ $\frac{1}{6}t^{3}$

因此有：

原式 $=$ $\lim_{x \rightarrow 0}$ $\frac{\frac{1}{6}t^{3}}{t^{3}}$ $=$ $\frac{1}{6}$

方法二

本题也可以结合使用等价无穷小与 $\frac{0}{0}$ 型洛必达等定理解出。

需要用到的等价无穷小有（当 $x$ $\rightarrow$ $0$ 时）：

$x$ $\sim$ $\sin x$;

$1$ $-$ $\cos x$ $\sim$ $\frac{1}{2}x^{2}$

需要用到的洛必达法则公式是：

$\lim_{x \rightarrow x_{0}}$ $\frac{f(x)}{g(x)}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{f'(x)}{g'(x)}$

需要用到的求导规则是：

$(\sin x)’$ $=$ $\cos x$;

$(u-v)’$ $=$ $u’$ $-$ $v’$;

$f'(x)$ $=$ $f'[g(x)]$ $g'(x)$.

解答思路如下：

由于，当 $x$ $\rightarrow$ $0$ 时，$\sin x$ $\sim x$, 于是有：

原式 $=$ $\lim_{x \rightarrow 0}$ $\frac{[\sin x-\sin(\sin x)]\sin x}{x^{3}\sin x}$ $=$ $\lim_{x \rightarrow0}$ $\frac{\sin x-\sin(\sin x)}{x^{3}}$ (1)

由于，当 $x$ $\rightarrow$ $0$ 时，有：

$\sin x$ $-$ $\sin(\sin x)$ $\rightarrow$ $0$, 且存在导数;

$x^{3}$ $\rightarrow$ $0$, 且存在导数.

因此，可以对 (1) 式使用洛必达法则：

原式 $=$ $\lim_{x\rightarrow0}$ $\frac{[\sin x-\sin(\sin x)]’}{(x^{3})’}$ $=$ $\lim_{x\rightarrow0}$ $\frac{\cos x-\cos(\sin x)\cos x}{3x^{2}}$

化简得：

原式 $=$ $\lim_{x\rightarrow0}$ $\frac{\cos[1-\cos(\sin x)]}{3x^{2}}$

由于，当 $x$ $\rightarrow$ $0$ 时，$\cos x$ $\rightarrow$ $1$, 因此，进一步化简得：

原式 $=$ $\lim_{x\rightarrow0}$ $\frac{1-\cos(\sin x)}{3x^{2}}$

使用等价无穷小进一步计算可得：

原式 $=$ $\lim_{x\rightarrow0}$ $\frac{\frac{1}{2}\sin^{2}x}{3x^{2}}$ $=$ $\frac{\frac{1}{2}}{3}$ $=$ $\frac{1}{6}$

方法一的手写作答：

方法二的手写作答：

EOF

一、题目

甲乙两人赛跑，计时开始时，甲在乙前方 $10$（单位：m）处. 图中，实线表示甲的速度曲线 $v$ $=$ $v_{1}(t)$ （单位 : m/s），虚线表示乙的速度曲线 $v$ $=$ $v_{2}(t)$ （单位 : m/s），三块阴影部分面积的数值依次为 $10$, $20$, $3$. 计时开始后乙追上甲的时刻记为 $t_{0}$ （单位 : s），则（）

( A ) $t_{0}$ $=$ $10$.

( B ) $15$ $<$ $t_{0}$ $<$ $20$.

( C ) $t_{0}$ $=$ $25$.

( D ) $t_{0}$ $>$ $25$.

二、解析

方法一

从物理学的角度，本题就是考查速度与路程的关系。

题目中给出的 $X$ $-$ $Y$ 坐标图像是“时间-速度”图像。那么，根据物理学知识我们知道，该曲线与坐标轴围成的图像的面积就是走过的路程。我们又知道，实线表示甲，虚线表示乙，而且刚开始时甲在乙前面 $10$ 米处。

由图像可知，当 $t$ $=$ $10$ 时，甲在乙前面 $20$ 米处，当 $t$ $=$ $25$ 时，乙在第 $10$ 秒到第 $25$ 秒之间的 $15$ 秒时间里比甲多跑了 $20$ 米，正好抵消了之前乙落后于甲的 $20$ 米路程。因此，当 $t$ $=$ $25$ 时，乙追上了甲，即 $t_{0}$ $=$ $25$。

综上可知，本题的正确选项是：$C$.

方法二

从数学的角度，本题主要考查的是定积分的基本运算和定积分的几何意义。

使用高等数学解答本题需要如下关于定积分的知识：

1. 定积分的几何意义：
   曲边梯形的代数和.
2. 定积分的基本性质：
   定积分的线性性：

$\int_{a}^{b}$ $[$ $k_{1}$ $f_{1}(x)$ $+$ $k_{2}$ $f_{2}(x)$ $]$ $dx$ $=$ $k_{1}$ $\int_{a}^{b}$ $f_{1}(x)$ $dx$ $+$ $k_{2}$ $\int_{a}^{b}$ $f_{2}(x)$ $dx$.

定积分积分区间的可加性：
$\int_{a}^{b}$ $f(x)$ $dx$ $=$ $\int_{a}^{c}$ $f(x)$ $dx$ $+$ $\int_{c}^{b}$ $f(x)$ $dx$.

根据上面的知识，我们可以做如下推理。

如果我们约定，使用 $v(t)$ 表示速度，使用 $s(t)$ 表示路程，那么在从 $0$ 到 $t$ 这个时间段内，可以写出如下定积分表达式：

$s(t)$ $=$ $\int_{0}^{t}$ $v(t)$ $dx$.

因此，当乙在 $t_{0}$ 时刻追上甲时，甲走过的路程为：

$s_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{1}(t)$.

乙走过的路程为：

$s_{2}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{2}(t)$.

$s_{2}(t)$

和 $s_{1}(t)$ 的关系为：

$s_{2}(t)$ $-$ $10$ $=$ $s_{1}(t)$.

于是有：

$s_{2}(t)$ $-$ $s_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{2}(t)$ $-$ $\int_{0}^{t_{0}}$ $v_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.

由于在从 $0$ 到 $10$ 秒的时间段内，$v_{2}$ 始终大于 $v_{1}$, 因此，乙超过甲的时间 $t_{0}$ 一定大于 $10$, 于是有：

$\int_{0}^{10}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $+$ $\int_{10}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.

又由于，从题中给出的图像我们可以看出：

$\int_{0}^{10}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.

因此有：

$\int_{10}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $20$. (1)

根据题中图像可知，在第 $10$ 秒到第 $25$ 秒这段时间里，图像中对应的阴影部分的面积为 $20$, 所以当 $t_{0}$ $=$ $25$ 时， $(1) $ 式成立。

综上可知，本题的正确选项是：$C$.

EOF

一、题目

已知函数 $f(x)$ $=$ $\frac{1}{1+x^{2}}$, 则 $f^{(3)}(0)$ $=$

二、解析

方法一

本题可以借助函数奇偶性的相关性质解出。

由于：

$f(x)$ $=$ $\frac{1}{1+x^{2}}$

$f(x)$ $=$ $\frac{1}{1+x^{2}}$

$f(-x)$ $=$ $\frac{1}{1+(-x)^{2}}$ $=$ $\frac{1}{1+x^{2}}$

因此：

$f(x)$ $=$ $f(-x)$

于是，我们知道，函数 $f(x)$ 是一个偶函数。

接下来，根据“偶函数的导数是奇函数，奇函数的导数是偶函数”的规律，我们知道，函数 $f^{(3)}(x)$ 是一个奇函数。

又由于，如果一个奇函数 $g(x)$ 在原点处$($ $x$ $=$ $0$ $)$有定义，则 $g(x)$ $=$ $0$, 因此有：

$f^{(3)}(0)$ $=$ $0$

综上可知，本题的答案就是：$0$.

方法二

本题也可以借助泰勒级数计算。

本题要求解的是在 $x$ $=$ $0$ 时，$f(x)$ 的三次导函数的函数值。我们知道，麦克劳林级数就是函数在 $x$ $=$ $0$ 处的泰勒级数，是泰勒级数的一个特例。于是，这里我们可以使用麦克劳林级数对原式进行级数展开。

麦克劳林级数中有一个关于几何级数的公式，如下：

$\frac{1}{1-x}$ $=$ $\sum_{0}^{\infty}$ $x^{n}$, $|x|$ $<$ $1$

当我们把上述公式中的 $x$ 替换成 $-x^{2}$ 后，$f(x)$ 就可以使用上述几何级数的公式表达，如下：

$f(x)$ $=$ $\frac{1}{1+x^{2}}$ $=$ $\frac{1}{1-(-x^{2})}$ $=$ $\sum_{0}^{\infty}$ $(-x^{2})^{n}$ $=$ $\sum_{0}^{\infty}$ $(-1)^{n}$ $x^{2n}$

之后，对 $f(x)$ 求导：

$f'(x)$ $=$ $\sum_{0}^{\infty}$ $(-1)^{n}$ $\cdot$ $2n$ $\cdot$ $x^{2n-1}$

$f”(x)$ $=$ $\sum_{0}^{\infty}$ $(-1)^{n}$ $\cdot$ $2n$ $\cdot$ $(2n-1)$ $\cdot$ $x^{2n-2}$

$f”'(x)$ $=$ $\sum_{0}^{\infty}$ $(-1)^{n}$ $\cdot$ $2n$ $\cdot$ $(2n-1)$ $\cdot$ $(2n-2)$ $\cdot$ $x^{2n-3}$

于是，$f”'(0)=0$.

综上可知，本题的答案就是： $0$.

EOF