题目
设随机变量 $Y$ 服从参数为 $1$ 的指数分布,$a$ 为常数且大于零,则 $P\{Y \leqslant a+1 | Y>a\}=$ __.
继续阅读“2013 年研究生入学考试数学一填空题第 6 题解析”设随机变量 $Y$ 服从参数为 $1$ 的指数分布,$a$ 为常数且大于零,则 $P\{Y \leqslant a+1 | Y>a\}=$ __.
继续阅读“2013 年研究生入学考试数学一填空题第 6 题解析”设二维随机变量 $(X,Y)$ 服从正态分布 $N(\mu,\mu;\sigma^{2},\sigma^{2};0),$ 则 $E(XY^{2})=$____.
由于在正态分布 $X \sim $ $N(\mu, \sigma^{2})$中 $E(X)=\mu$, $D(X)=\sigma^{2}.$ 而且二维正态分布中依然遵循这一定理。
于是,根据题目中的条件我们知道,$E(X)=$ $E(Y)=\mu$, $D(X)=$ $D(Y)=$ $\sigma^{2}.$
又由 $\rho=0$ 我们知道,$X$ 与 $Y$ 相互独立。根据随机变量的独立性中的如下性质:
若 $X_{1},X_{2},$ $\dots ,$ $ X_{n},$ $Y_{1},$ $Y_{2},$ $\dots ,$ $ Y_{m}$ 相互独立,$f(\cdot)$ 为 $n$ 元连续函数且 $g(\cdot)$ 为 $m$ 元连续函数,则 $f(X_{1},X_{2}, \cdots , X_{n})$ 与 $g(X_{1},X_{2}, \cdots , X_{m})$ 也相互独立。
因此,我们知道,$X$ 与 $Y^{2}$ 也相互独立,于是有:
$E(XY^{2})=$ $E(X)E(Y^{2})=$ $E(X) \times [D(Y)+E^{2}(Y)]=$ $\mu(\sigma^{2}+\mu^{2}).$
综上可知,本题的正确答案是:$\mu(\sigma^{2}+\mu^{2})$.
EOF
设 $A,B,C$ 是随机事件,$A$ 与 $C$ 互不相容,$P(AB)$ $=$ $\frac{1}{2}$, $P(C)$ $=$ $\frac{1}{3}$, 则 $P(AB|\bar{C})$ $=$__.
$A$与 $C$ 互不相容 $\Rightarrow$ $A$ $\cap$ $C$ $=$ $\phi$ $\Rightarrow$ $P(AC)$ $=$ $P(\phi)$ $=$ $P(\phi \cap B)$ $\Rightarrow$ $P(AC \cap B)$ $=$ $0$.
于是,我们有:
$P(AB|\bar{C})$ $=$ $\frac{P(AB \bar{C})}{P(\bar{C})}$ $=$ $\frac{P[AB(1-C)]}{1-P(C)}$ $=$ $\frac{P(AB-ABC)}{1-P(C)}$ $=$ $\frac{P(AB)-P(AB \cap ABC)}{1-P(C)}$ $=$ $\frac{P(AB)-P(ABC)}{1-P(C)}$ $=$ $\frac{\frac{1}{2}-0}{\frac{2}{3}}$ $=$ $\frac{1}{2}$ $\times$ $\frac{3}{2}$ $=$ $\frac{3}{4}$.
综上可知,正确答案:$\frac{3}{4}$.
EOF
设随机变量 $X$ 服从参数为 $1$ 的泊松分布,则 $P {X=E(X^{2})}$ $=$__.
每年考研数学一试卷中填空题的最后一题基本都是考一个概率论中的知识。本题考察的知识很明确,就是:泊松分布。
泊松分布的概念如下:
设随机变量 $X$ 的概率分布为:
$P {X=k}$ $=$ $\frac{\lambda^{k}e^{-\lambda}}{k!}$ $(\lambda>0,k=0,1,2,3 \dots)$
则称 $X$ 服从参数为 $\lambda$ 的泊松分布,记为 $X$ $\backsim$ $P(\lambda)$.
此外,在泊松分布中,数学期望 $E(X)$ $=$ $\lambda$, 方差 $D(X)$ $=$ $\lambda$.
最后,我们还需要知道 $E(X)$ 与 $D(X)$ 的关系公式:
$D(X)$ $=$ $E(X^{2})$ $-$ $[E(X)]^{2}$.
由题目信息可知,该题中泊松分布的参数 $\lambda=1$, 于是我们知道:
$E(X)$ $=$ $D(X)$ $=$ $1$.
由于题目中要求的表达式中含有 “$E(X^{2})$”, 而在 $E(X)$ 与 $D(X)$ 的关系式中也含有 “$E(X^{2})$”, 于是,我们有:
$E(X^{2})$ $=$ $D(X)$ $+$ $[E(X)]^{2}$.
进而有:
$E(X^{2})$ $=$ $1$ $+$ $1^{2}$ $=$ $1$ $+$ $1$ $=$ $2$.
于是,我们要求的表达式就变成了:
$P{X=E(X^{2})}$ $\Rightarrow$ $P{X=2}$.
至此,我们已经知道了泊松分布的计算公式中的两个未知量的数值,分别是:
$\lambda$ $=$ $1$, $k$ $=$ $E(X^{2})$ $=$ $2$.
于是,根据泊松分布的计算公式,我们有:
$P$ $=$ $\frac{\lambda^{k}e^{-\lambda}}{k!}$ $=$ $\frac{1^{2}e^{-1}}{2!}$ $=$ $\frac{e^{-1}}{2 \times 1}$ $=$ $\frac{1}{e}$ $\times$ $\frac{1}{2}$ $=$ $\frac{1}{2e}$.
综上可知,正确答案就是:$\frac{1}{2e}$.
EOF
设随机事件 $A$ 与 $B$ 相互独立,且 $P(B)$ $=$ $0.5$ ,$P(A-B)$ $=$ $0.3$, 则 $P(B-A)$ $=$ ( )
( A ) $0.1$
( B ) $0.2$
( C ) $0.3$
( D ) $0.4$
本题的关键点是“相互独立”,即 $A$ 事件与 $B$ 事件是两个相互独立的事件,$A$ 事件的发生不会影响 $B$, $B$ 事件的发生也不会影响 $A$. 由于 $A$ 事件的发生与否都不影响 $B$ 事件的发生与否,由此我们知道,若 $A$ 与 $B$ 相互独立,那么 $A$ 与 $\bar{B}$ 也相互独立,$B$ 与 $\bar{A}$ 同样相互独立。因此,我们可以在接下来的计算中,使用带有 $\bar{A}$ 和 $\bar{B}$ 的式子代替带有 $A$ 与 $B$ 的式子进行化简。
根据概率论中关于事件的独立性方面的相关知识,我们知道:
$A$与 $B$ 相互独立 $\Leftrightarrow$ $P(AB)$ $=$ $P(A)P(B)$.
综上,于是有:
$P(AB)$ $=$ $P(A)P(B)$;
$P(A \bar{B})$ $=$ $P(A)P(\bar{B})$;
$P(\bar{A}B)$ $=$ $P(\bar{A})P(B)$;
根据概率论减法公式,我们知道(这个公式没有设置 $A$ 和 $B$ 的关系,即是说,只要 $A$ 和 $B$ 是两个事件就是用这个公式计算,自然也可以应用于相互独立的事件。):
$P(B-A)$ $=$ $P(B)$ $-$ $P(AB)$.
题目中给出的条件有:
$P(B)$ $=$ $0.5$, $P(A-B)$ $=$ $0.3$
根据逆事件(对立事件)的知识,我们还知道:
$P(\bar{B})$ $=$ $1$ $-$ $P(B)$ $=$ $0.5$;
$P(B)$ $=$ $1$ $-$ $P(\bar{B})$ $=$ $0.5$.
于是,将 $P(A-B)$ 中的 $B$ 用 $\bar{B}$ 替换后得到:
$P(A-B)$ $=$ $P(A)$ $-$ $P(AB)$ $=$ $P(A)$ $-$ $P[A(1-\bar{B})]$ $=$ $P(A)$ $-$ $P(A-A \bar{B})$ $=$ $P(A)$ $-$ $[P(A)$ $-$ $P(AA \bar{B})]$ $=$ $P(A)$ $-$ $P(A)$ $+$ $P(A \bar{B})$ $=$ $P(A \bar{B})$ $=$ $P(A)P(\bar{B})$ $=$ $P(A)$ $\cdot$ $0.5$ $=$ $0.3$.
注:由于 $A$ $\cap$ $A$ $=$ $A$, 即 $AA$ $=$ $A$, 所以:$P(A)$ $-$ $P(AA \bar{B})$ $=$ $P(A)$ $-$ $P(A \bar{B})$, 下面的类似计算过程中将省略这一步。
于是有:$P(A)$ $=$ $\frac{0.3}{0.5}$ $=$ $0.6$.
又因为:
$P(B-A)$ $=$ $P(B)$ $-$ $P(AB)$ $=$ $P(B)$ $-$ $P[(1- \bar{A})B]$ $=$ $P(B)$ $-$ $P(B-\bar{A}B)$ $=$ $P(B)$ $-$ $P(B)$ $+$ $P(\bar{A}B)$ $=$ $P(\bar{A}B)$ $=$ $P(\bar{A})P(B)$.
由于,$P(A)$ $=$ $0.6$, 则,$P(\bar{A})$ $=$ $0.4$.
于是有:
$P(B-A)$ $=$ $P(\bar{A})P(B)$ $=$ $0.4$ $\cdot$ $0.5$ $=$ $0.2$.
综上可知,本题的正确选项是:$B$.
本文开头提到了,本题的关键点是“相互独立”。如果没有注意到这个关键点会发生什么呢?没有注意到这个关键点的话,可能会出现如下错误的思考方式和解法。
在概率论中有一个公式是下面这样的:
$P(B-A)$ $=$ $P(B)$ $-$ $P(A)$.
如果根据这个公式计算,那么本题将十分简单(数学一中也不会出这么“直观”的题吧 :-)):
已知:$P(B)$ $=$ $0.5$, $P(A-B)$ $=$ $0.3$, 那么:
$P(A-B)$ $=$ $P(A)$ $-$ $P(B)$ $=$ $P(A)$ $-$ $0.5$ $=$ $0.3$ $\Rightarrow$ $P(A)$ $=$ $0.8$ $\Rightarrow$ $P(B-A)$ $=$ $P(B)$ $-$ $P(A)$ $=$ $0.5$ $-$ $0.8$ $=$ $-0.3$.
但是,我们观察选项可知,并没有哪个选项是 $-0.3$, 而且 $P(B-A)$ $=$ $P(B)$ $-$ $P(A)$ 这个公式是有前提条件的,那就是:
很显然,在独立事件中,不可能出现 $A$ $\subset$ $B$ 或者 $B$ $\subset$ $A$ 的情况。
因此我们知道,在使用一个公式前,一定要仔细审查,确保该公式的适用范围符合当前的解题环境,不能只是因为题目中的参数可以和公式中的参数对应就直接拿来使用。
EOF
若 $A$, $B$ 为任意两个随机事件,则 ( )
( A ) $P(AB)$ $\leqslant$ $P(A)P(B)$.
( B ) $P(AB)$ $\geqslant$ $P(A)P(B)$.
( C ) $P(AB)$ $\leqslant$ $\frac{P(A)+P(B)}{2}$.
( D ) $P(AB)$ $\geqslant$ $\frac{P(A)+P(B)}{2}$.
我们知道,$AB$ $\Leftrightarrow$ $A$ $\cap$ $B$.
于是,我们知道,$AB$ $\subset$ $A$, $AB$ $\subset$ $B$.
接下来,根据概率的基本性质中的可比性:
设 $A$, $B$ 是两个事件,若 $A$ $\subset$ $B$, 则有:
$P(A)$ $\leqslant$ $P(B)$;
$P(B-A)$ $=$ $P(B)$ $-$ $P(A)$.
于是,我们知道:
$P(AB)$ $\leqslant$ $P(A)$; ①
$P(AB)$ $\leqslant$ $P(B)$. ②
接下来,将 ① 式与 ② 式联立可得:
$P(AB)$ $+$ $P(AB)$ $\leqslant$ $P(A)$ $+$ $P(B)$ $\Leftrightarrow$ $2$ $\cdot$ $P(AB)$ $\leqslant$ $P(A)$ $+$ $P(B)$ $\Leftrightarrow$ $P(AB)$ $\leqslant$ $\frac{P(A)+P(B)}{2}$.
综上可知,本题的正确选项是:$C$.
EOF
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续,其 $2$ 阶导函数 $f”(x)$ 的图形如图 1 所示,则曲线 $y$ $=$ $f(x)$ 的拐点的个数为 ( )
( A ) $0$.
( B ) $1$.
( C ) $2$.
( D ) $3$.
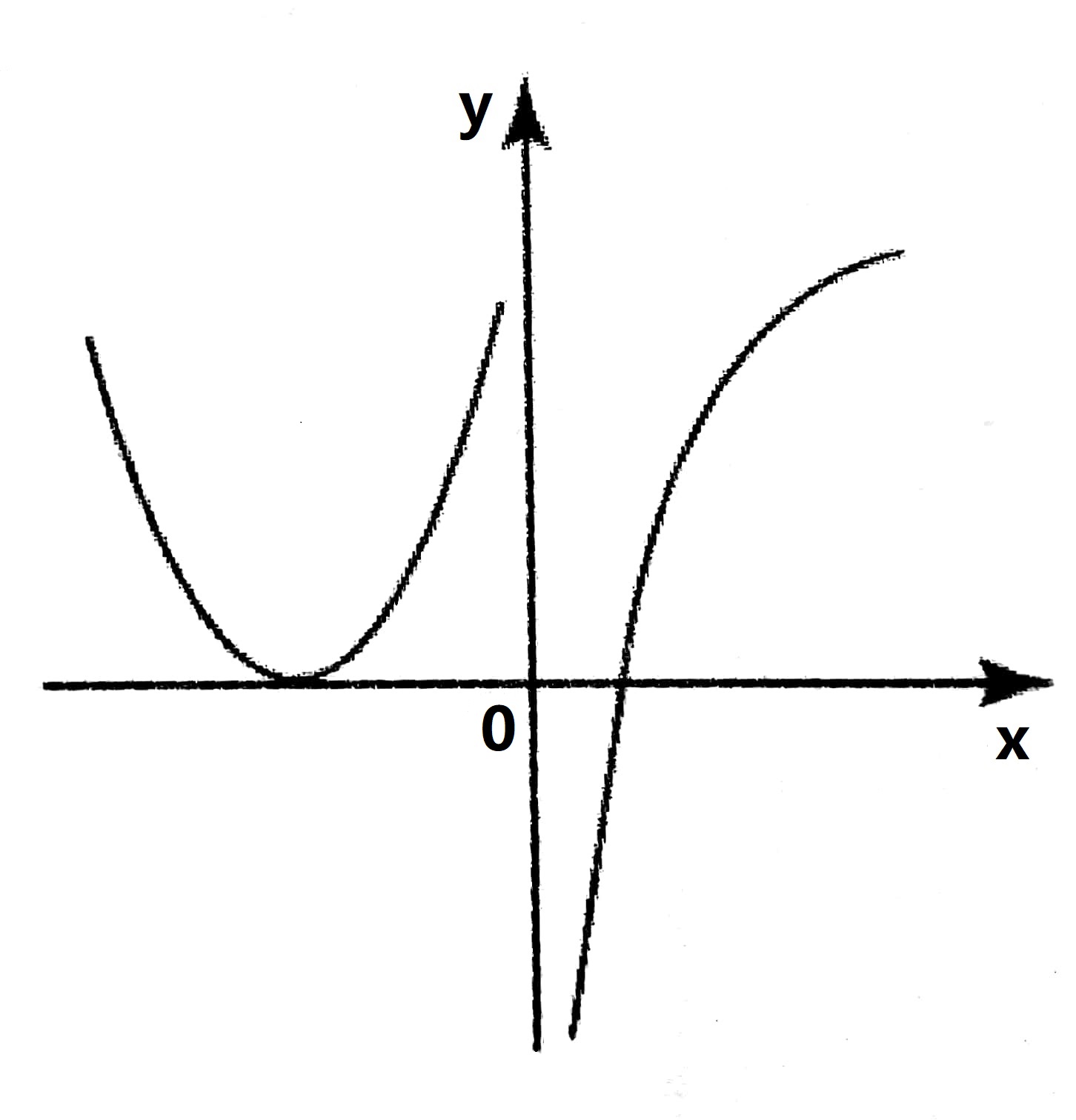
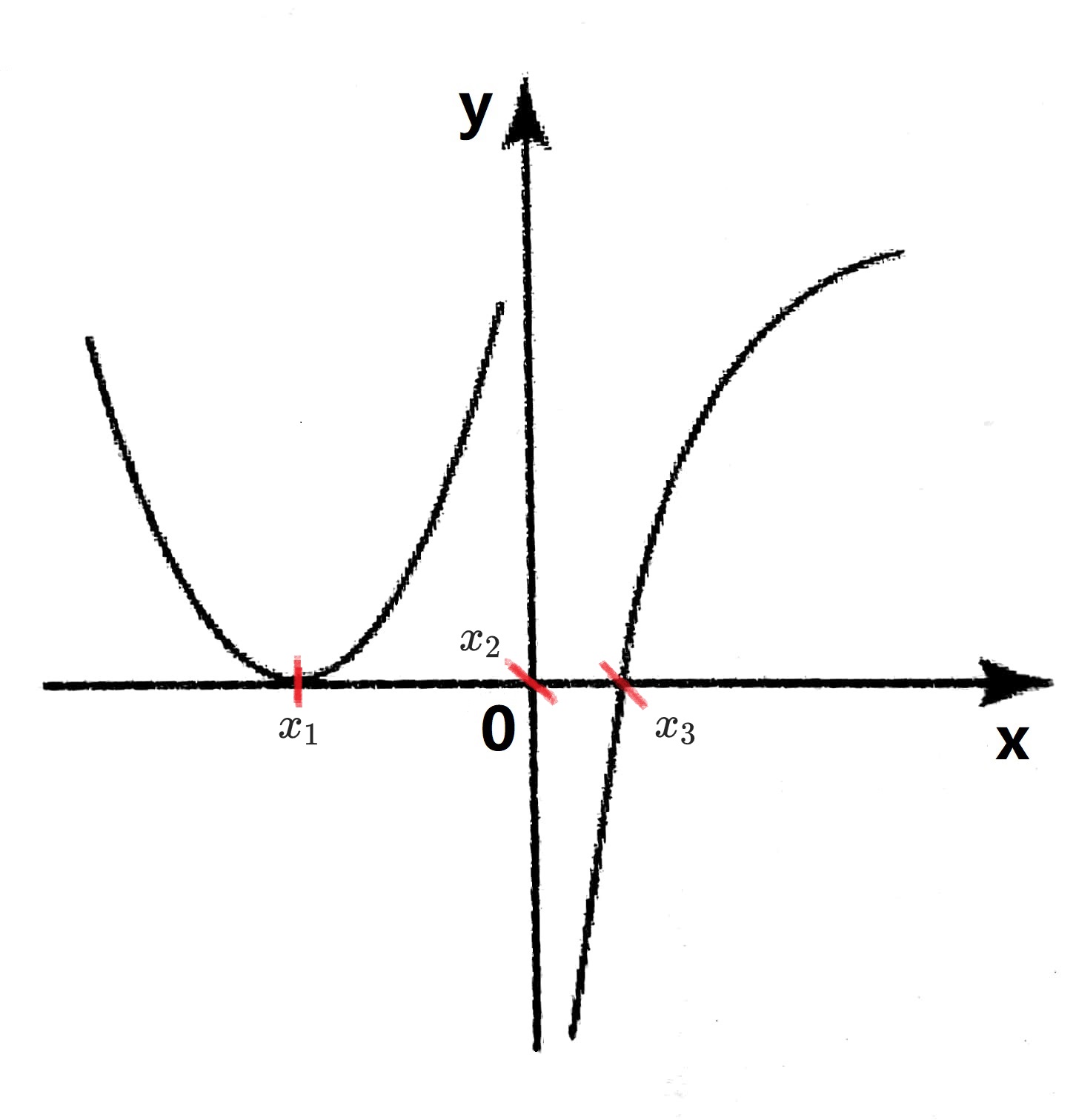
如图 2 所示,令左边的曲线与 $x$ 轴的交点为点 $x_{1}$, 坐标原点为点 $x_{2}$, 右边曲线与 $x$ 轴的交点为点 $x_{3}$:
由于本题涉及 2 阶导数,因此可以通过拐点存在的充分条件中的第一充分条件来判定:
若曲线 $y$ $=$ $f(x)$ 在 $x$ $=$ $x_{0}$ 处 $f”(x_{0})$ $=$ $0$ (或 $f”(x_{0})$ 不存在,但 $f(x)$ 在 $x$ $=$ $x_{0}$ 处连续),若 $f”(x)$ 在 $x_{0}$ 的左、右两侧邻域内异号,则 $(x_{0}$, $f(x_{0}))$ 为曲线 $y$ $=$ $f(x)$ 的拐点。
我们知道,对于连续函数的图像曲线而言,拐点处的图像曲线要么等于零,要么不存在。图 2 中的 $x_{1}$, $x_{2}$, $x_{3}$ ( $f”(x_{2})$ 虽然不存在,但是由题目中给出的“函数 $f(x)$ 在 $(-\infty,+\infty)$ 上连续”的条件我们知道,$f”(x_{2})$ 在点 $x_{2}$ 的左右两侧邻域是连续的,可能是原函数的一个拐点。)三个点均满足该条件。但是点 $x_{1}$ 两侧的函数都为正($f”(x)$ 的图像在 $x$ 轴上方),因此,不满足“左右两侧邻域内异号”的条件,因此,点 $x_{1}$ 不是函数 $f(x)$ 的拐点。点 $x_{2}$ 和 $x_{3}$ 两侧邻域的函数图像均异号,因此点 $x_{2}$ 和 $x_{3}$ 满足函数拐点存在的充分条件,函数 $f(x)$ 有两个拐点。
综上可知,本题的正确选项是:$C$.
EOF
曲线 $y$ $=$ $(x-1)$ $(x-2)^{2}$ $(x-3)^{3}$ $(x-4)^{4}$ 的拐点是 ( )
( A ) $(1,0)$.
( B ) $(2,0)$.
( C ) $(3,0)$.
( D ) $(4,0)$.
本题主要涉及求导,曲线的凹凸性,曲线凹凸性的判定,拐点的定义,拐点存在的充分条件这些知识。
曲线凹凸性的定义如下:
设函数 $f(x)$ 在区间 $I$ 上连续,若对 $I$ 上任意两点 $x_{1}$, $x_{2}$, 恒有:
$f(\frac{x_{1}+x_{2}}{2})$ $<$ $(>)$ $\frac{f(x_{1})+f(x_{2})}{2}$,
则称曲线 $y$ $=$ $f(x)$ 在区间 $I$ 上是向凹(凸)的.
曲线凹凸性的判定如下:
设函数 $f(x)$ 在 $[a,b]$ 上连续,在 $(a,b)$ 内具有二阶导数,那么:
① 如果在 $(a,b)$ 内 $f”(x)$ $>$ $0$, 则曲线 $y$ $=$ $f(x)$ 在 $[a,b]$ 上是凹的;
② 如果在 $(a,b)$ 内 $f”(x)$ $<$ $0$, 则曲线 $y$ $=$ $f(x)$ 在 $[a,b]$ 上是凸的.
拐点的定义如下:
设函数 $f(x)$ 在区间 $I$ 内连续,$x_{0}$ 是 $I$ 的内点,如果曲线 $y$ $=$ $f(x)$ 在经过点 $(x_{0},$ $f(x_{0}))$ 时凹凸性发生了改变,则称点 $(x_{0},$ $f(x_{0}))$ 为曲线的拐点.
拐点存在的充分条件如下:
第一充分条件:若曲线 $y$ $=$ $f(x)$ 在 $x$ $=$ $x_{0}$ 处 $f”(x_{0})$ $=0$ (或 $f”(x_{0})$ 不存在,但 $f(x)$ 在 $x$ $=$ $x_{0}$ 处连续),若 $f”(x)$ 在 $x_{0}$ 的左右两侧邻域异号,则 $(x_{0},$ $f(x_{0}))$ 为曲线 $y$ $=$ $f(x)$的拐点.
第二充分条件:设 $f(x)$ 在 $x$ $=$ $x_{0}$ 的某邻域内有三阶导数,且 $f”(x_{0})$ $=$ $0$, $f”'(x_{0})$ $\neq$ $0$, 则 $(x_{0},$ $f(x_{0}))$ 为 $f(x)$ 的拐点.
回到本题。本题的原式是:
$y$ $=$ $(x-1)$ $(x-2)^{2}$ $(x-3)^{3}$ $(x-4)^{4}$.
观察可知,当 $x$ $=$ $1$, $2$, $3$, $4$ 时都可以使 $y$ $=$ $0$, 而我们在找拐点的时候,最重要的就是找到哪个点是大于零的,哪个点是小于零的或者哪个点是等于零的,上面式子的设定从计算上来看可以很快地找到这些特殊点。
求拐点的过程中少不了要计算导数,但是上面的式子太长,求导之后会更长,为了方便计算,尽可能避免出错,我们作如下约定:
令:
$A$ $=$ $(x-1)$;
$B$ $=$ $(x-2)^{2}$;
$C$ $=$ $(x-3)^{3}$;
$D$ $=$ $(x-4)^{4}$.
之后,我们有:
原式 $=$ $y$ $=$ $ABCD$.
于是我们有:
$y’$ $=$ $A’BCD$ $+$ $A(BCD)’$;
$y”$ $=$ $A”BCD$ $+$ $A'(BCD)’$ $+$ $A'(BCD)’$ $+$ $A(BCD)”$;
$y”’$ $=$ $A”’BCD$ $+$ $A”(BCD)’$ $+$ $A”(BCD)’$ $+$ $A'(BCD)”$ $+$ $A”(BCD)’$ $+$ $A’BCD”$ $+$ $A'(BCD)”$ $+$ $A(BCD)”’$;
令 $y’$ $=$ $0$, 则有:
$y'(2)$ $=$ $y'(3)$ $=$ $y'(4)$ $=$ $0$;
$y'(1)$ $\neq$ $0$. ($x$ $=$ $1$ 对应 $A$, 但是 $A’$ 是一个常数,不受 $x$ 的影响,因此 $x$ $=$ $1$ 不会使 $y’$ $=$ $0$, 以下计算过程中的判断与此类似.)
令 $y”$ $=$ $0$, 则有:
$y”(3)$ $=$ $y”(4)$ $=$ $0$;
$y”(1)$ $\neq$ $0$, $y”(2)$ $\neq$ $0$.
令 $y”’$ $=$ $0$, 则有:
$y”'(4)$ $=$ $0$;
$y”'(1)$ $\neq$ $0$, $y”'(2)$ $\neq$ $0$, $y”'(3)$ $\neq$ $0$.
通过上面的计算我们知道,$y”(3)$ $=$ $0$ 且 $y”'(3)$ $\neq$ $0$, 因此,根据拐点存在的充分条件中的第二充分条件,点 $(3,0)$ 是曲线 $y$ 的拐点。
综上可知,本题的正确选项是:C
EOF
当 $x$ $\rightarrow$ $0$ 时,$f(x)$ $=$ $x$ $-$ $\sin ax$ 与 $g(x)$ $=$ $x^{2}$ $\ln(1-bx)$ 是等价无穷小,则()
( A ) $a$ $=$ $1$, $b$ $=$ $-$ $\frac{1}{6}$.
( B ) $a$ $=$ $1$, $b$ $=$ $\frac{1}{6}$.
( C ) $a$ $=$ $-1$, $b$ $=$ $-\frac{1}{6}$.
( D ) $a$ $=$ $-1$, $b$ $=$ $\frac{1}{6}$.
由于 $f(x)$ 和 $g(x)$ 是等价无穷小,因此,根据“无穷小的比较”中关于等价无穷小的定理:
设 $\lim$ $\alpha(x)$ $=$ $0$, $\lim$ $\beta(x)$ $=$ $0$,
若 $\lim$ $\frac{\alpha (x)}{\beta (x)}$ $=$ $1$, 则 $\alpha(x)$ 与 $\beta(x)$ 是等价无穷小,记为 $\alpha(x)$ $\sim \beta(x)$.
因此,我们有:
$\lim_{x \rightarrow 0}$ $\frac{f(x)}{g(x)}$ $=$ $\lim_{x\rightarrow 0}$ $\frac{x-\sin ax}{x^{2}\ln(1-bx)}$ $=$ $1$.
在“常用的等价无穷小”中,同时和 $\sin x$ 与 $x$ 有关的等价无穷小两个,如下:
$\sin x$ $\sim x$;
$x$ $-$ $\sin x$ $\sim$ $\frac{1}{6}x^{3}$.
同时和 $\ln x$ 与 $x$ 有关的等价无穷小也有两个,如下:
$\ln(1+x)$ $\sim x$;
$x$ $-$ $\ln(1+x)$ $\sim$ $\frac{1}{2}x^{2}$.
那么,我们现在需要考虑的问题就是:需要组合使用哪两个等价无穷小化简原式?
这里选择并确定使用哪两个等价无穷小的依据就是题目中给出的“等价无穷小”。也就是说,在对原式进行化简运算的过程中,必须保证分子分母互为等价无穷小,每一步都要遵守这个原则,最后化简出来的结果中分子分母也必须互为等价无穷小,只有这样才可以和原式划等号。
由前面的计算我们知道,原式的分子是:
$x$ $-$ $\sin ax$
原式的分母是:
$x^{2}$ $\ln(1-bx)$
于是,分子的有效化简形式有以下四种:
$x$ $-$ $\sin ax$ $=$ $x$ $-$ $ax$ (1)
或者:
$x$ $-$ $\sin ax$ $=$ $\sin x$ $-$ $\sin ax$ (2)
或者:
$x$ $-$ $\sin ax$ $=$ $x$ $-$ $[ax$ $-$ $\frac{1}{6}$ $(ax)^{3}]$ $=$ $x$ $-$ $ax$ $+$ $\frac{1}{6}$ $a^{3}$ $x^{3}$ (3)
或者:
$x$ $-$ $\sin ax$ $=$ $\frac{1}{6}x^{3}$ $+$ $\sin x$ $-$ $\sin ax$ (4)
分母的有效化简形式有以下两种:
$x^{2}$ $\ln(1-bx)$ $=$ $x^{2}$ $(-bx)$ $=$ $-bx^{3}$ (5)
或者:
$x^{2}$ $\ln(1-bx)$ $=$ $x^{2}$ $[(-bx)$ $-$ $\frac{1}{2}$ $(-bx)^{2}]$ $=$ $-bx^{3}$ $-$ $\frac{1}{2}$ $b^{2}$ $x^{4}$ (6)
由于要保证每一步计算过程中分子分母都是等价无穷小,因此,我们首先要看看那些式子组合起来可以形成等价无穷小。
(1) 到 (6) 六个式子中变量 $x$ 的次方数情况如下:
(1): 只包含 $1$ 次方;
(2): 只包含 $1$ 次方;
(3): 包含 $1$ 次方和 $3$ 次方;
(4): 包含 $1$ 次方和 $3$ 次方;
(5): 只包含 $3$ 次方;
(6): 包含 $3$ 次方和 $4$ 次方。
由于分母对应的 (5) 和 (6) 两个式子都包含 $3$ 次方,分子对应的 (1) 式和 (2) 式无论如何变化也不会出现 $3$ 次方,无法与分母构成等价无穷小,因此排除。此外,(4) 式有 $\sin x$ 和 $\sin ax$, 而分母中并没有对应的形式,因此 (4) 式被基本排除。
现在就剩下分子对应的 (3) 式和分母对应的 (5) 式和 (6) 式了。由于 (6) 式中含有 $x$ 的 4 次方,而 (3) 式无论如何变化也不会出现 4 次方,因此,正确的化简过程应该在 (3) 式和 (5) 式中产生。
基于以上分析,尝试化简如下:
原式 $=$ $\lim_{x\rightarrow 0}$ $\frac{x-ax+\frac{1}{6}a^{3}x^{3}}{-bx^{3}}$ $=$ $\lim_{x\rightarrow0}$ $\frac{(1-a)x+\frac{1}{6}a^{3}x^{3}}{-bx^{3}}$
分母中没有 $1$ 次方,因此,为了保证“分子分母互为等价无穷小”这个条件始终成立,唯一的办法就是令 $1$ $-$ $a$ $=0$, 接下来,根据 $f(x)$ $\sim$ $g(x)$ 所得的分子分母的对应关系,我们可以得到:
$\frac{1}{6}a^{3}$ $=$ $-b$
两式联立:
$\left\{\begin{matrix}1-a=0,\\ \frac{1}{6}a^{3}=-b.\end{matrix}\right.$
解得:
$\left\{\begin{matrix} a=1,\\ b=-\frac{1}{6}.\end{matrix}\right.$
综上可知,本题的正确选项是:$A$
通过本题,我们可以总结出使用等价无穷小化简原式过程中的以下规律:
曲线 $\sin (xy)$ $+$ $\ln(y-x)$ $=x$ 在点 $(0,1)$ 处的切线方程为__.
本题需要用到求导法则和切线方程公式的相关知识。
需要用到的求导公式有:
$(\sin x)’$ $=$ $\cos x$;
$(\ln x)’$ $=$ $\frac{1}{x}$;
$(ab)’$ $=$ $a’b$ $+$ $ab’$;
$f'(x)$ $=$ $f'[\phi(x)]$ $\cdot$ $\phi'(x)$.
求导过程中另外需要注意的两点如下:
切线方程的计算公式如下:
$y$ $-$ $f(x_{0})$ $=$ $f'(x_{0})$ $(x-x_{0})$.
解答思路如下:
由于切线方程的计算公式中包含导数 $f'(x)$,因此,首先需要计算出导数。原式两边同时对 $x$ 求导可以产生导数 $y’$:
$[\sin(xy)$ $+$ $\ln(y-x)]’$ $=$ $(x)’$ $\Rightarrow$ $\cos(xy)$ $(x’y+xy’)$ $+$ $\frac{1}{y-x}$ $(y-x)’$ $=$ $1$ $\Rightarrow$ $\cos(xy)$ $(y$ $+$ $xy’$ $)$ $+$ $\frac{1}{y-x}$ $(y’$ $-$ $1$ $)$ $=$ $1$.
要求的是曲线在点 $(0,1)$ 处的切线方程,因此,我们把 $x$ $=$ $0$; $y$ $=$ $1$带入上面的到的式子中,得:
$1$ $\cdot$ $1$ $+$ $1$ $\cdot$ $(y’$ $-$ $1$ $)$ $=$ $1$ $\Rightarrow$ $1$ $+$ $y’$ $-$ $1$ $=$ $1$ $\Rightarrow$ $y’$ $=$ $1$.
即:
$y'(0)$ $=$ $1$.
将上述结果带入切线方程求导公式得:
$y$ $-$ $1$ $=$ $1$ $\cdot$ $($ $x$ $-$ $0$ $)$ $\Rightarrow$ $y$ $=$ $x$ $+$ $1$.
综上可知,本题得答案是:$y$ $=$ $x$ $+$ $1$.
EOF
设函数 $f(x)$ $=$ $\int_{0}^{x^{2}}$ $\ln(2+t)$ $dt$, 则 $f'(x)$ 的零点个数()
( A ) $0$.
( B ) $1$.
( C ) $2$.
( D ) $3$.
本题可以使用积分和导数的相关定理解出。
涉及到的积分知识如下:
(1) 定积分基本性质
$\int_{a}^{b}$ $f(x)$ $dx$ $=$ $\int_{a}^{b}$ $f(t)dt$;
(2) 变上限积分函数求导
$F'(x)$ $=$ $f[\phi(x)]$ $\cdot$ $\phi'(x)$.
涉及到的求导知识如下:
$(x^{a})’$ $=$ $ax^{a-1}$;
此外,我们需要知道的是,“函数零点”指的是 $f(x)$ $=$ $0$ 时,对应的自变量 $x$ 的数值,“函数零点” 不是一个点,而是一个数值。
解题思路如下:
根据变上限积分函数求导法则,有:
$f'(x)$ $=$ $\ln(2+x^{2})$ $\cdot$ $(x^{2})’$ $=$ $2$ $x$ $\ln(2+x^{2})$.
则要求函数 $f'(x)$ 的零点的个数,就是求 $2$ $x$ $\ln(2+x^{2})$ $=$ $0$ 的解的个数。
要使 $2$ $x$ $\ln(2+x^{2})$ $=$ $0$ 成立,则有以下三种情况(分情况讨论时要注意“不重不漏”):
(1) $2$ $x$ $=$ $0$ 且 $\ln(2+x^{2})$ $\neq$ $0$
此时解出 $x$ $=$ $0$.
(2) $2$ $x$ $\neq$ $0$ 且 $\ln(2+x^{2})$ $=$ $0$.
无解。
由于 $1$ $+$ $x^{2}$ $\geq$ $2$ 始终成立,而且当 $x$ $=$ $1$ 时,$\ln(x)$ $=$ $0$, 当 $x$ $>$ $1$ 时,$\ln(x)$ $>$ $0$.
所以,$\ln(2+x^{2})$ $>$ $0$ 始终成立,与 $x$ 轴没有交点。
(3) $2$ $x$ $=$ $0$ 且 $\ln(2+x^{2})$ $=$ $0$
$2$ $x$ $=$ $\ln(2+x^{2})$ $=$ $0$ $\Rightarrow$ 无解.
综上可知,当 $2$ $x$ $\ln(2+x^{2})$ $=$ $0$ 时,有:
$x$ $=$ $0$.
因此,只有一个零点,答案是:$B$.
EOF
求极限 $\lim_{x \rightarrow 0}$ $\frac{[\sin x-\sin (\sin x)] \sin x}{x^{4}}$
当题目中要求的是“极限”,而且出现了 $x$ $\rightarrow$ $0$ 时就要考虑是不是要用到或者可以用到等价无穷小。
还需要考虑的可能用到的知识是洛必达法则。当 $x$ $\rightarrow$ $0$ 时可能产生 $\frac{0}{0}$ 型的洛必达或者 $\frac{\infty}{\infty}$ 型的洛必达。而且,洛必达法则就是为求极限而生的,可以把对函数的求极限转换成对函数的导数求极限,从而可能化简原式。
本题考查的是等价无穷小,需要用到的两个等价无穷小如下(当 $x$ $\rightarrow$ $0$ 时):
$x$ $\sim$ $\sin x$;
$x$ $-$ $\sin x$ $\sim$ $\frac{1}{6}x^{3}$.
于是有:
原式 $=$ $\lim_{x \rightarrow 0}$ $\frac{[\sin x-\sin (\sin x)]\sin x}{\sin^{4}x}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{\sin x-\sin(\sin x)}{\sin^{3} x}$
令 $\sin x$ $=$ $t$, 则有:
原式 $=$ $\lim_{x \rightarrow 0}$ $\frac{t-\sin(t)}{t^{3}}$
由于,当 $x$ $\rightarrow$ $0$ 时,$\sin x$ $\rightarrow$ $0$, 于是有 $t$ $\rightarrow$ $0$, 因此根据常见的等价无穷小,有:
$t$ $-$ $\sin t$ $\sim$ $\frac{1}{6}t^{3}$
因此有:
原式 $=$ $\lim_{x \rightarrow 0}$ $\frac{\frac{1}{6}t^{3}}{t^{3}}$ $=$ $\frac{1}{6}$
本题也可以结合使用等价无穷小与 $\frac{0}{0}$ 型洛必达等定理解出。
需要用到的等价无穷小有(当 $x$ $\rightarrow$ $0$ 时):
$x$ $\sim$ $\sin x$;
$1$ $-$ $\cos x$ $\sim$ $\frac{1}{2}x^{2}$
需要用到的洛必达法则公式是:
$\lim_{x \rightarrow x_{0}}$ $\frac{f(x)}{g(x)}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{f'(x)}{g'(x)}$
需要用到的求导规则是:
$(\sin x)’$ $=$ $\cos x$;
$(u-v)’$ $=$ $u’$ $-$ $v’$;
$f'(x)$ $=$ $f'[g(x)]$ $g'(x)$.
解答思路如下:
由于,当 $x$ $\rightarrow$ $0$ 时,$\sin x$ $\sim x$, 于是有:
原式 $=$ $\lim_{x \rightarrow 0}$ $\frac{[\sin x-\sin(\sin x)]\sin x}{x^{3}\sin x}$ $=$ $\lim_{x \rightarrow0}$ $\frac{\sin x-\sin(\sin x)}{x^{3}}$ (1)
由于,当 $x$ $\rightarrow$ $0$ 时,有:
$\sin x$ $-$ $\sin(\sin x)$ $\rightarrow$ $0$, 且存在导数;
$x^{3}$ $\rightarrow$ $0$, 且存在导数.
因此,可以对 (1) 式使用洛必达法则:
原式 $=$ $\lim_{x\rightarrow0}$ $\frac{[\sin x-\sin(\sin x)]’}{(x^{3})’}$ $=$ $\lim_{x\rightarrow0}$ $\frac{\cos x-\cos(\sin x)\cos x}{3x^{2}}$
化简得:
原式 $=$ $\lim_{x\rightarrow0}$ $\frac{\cos[1-\cos(\sin x)]}{3x^{2}}$
由于,当 $x$ $\rightarrow$ $0$ 时,$\cos x$ $\rightarrow$ $1$, 因此,进一步化简得:
原式 $=$ $\lim_{x\rightarrow0}$ $\frac{1-\cos(\sin x)}{3x^{2}}$
使用等价无穷小进一步计算可得:
原式 $=$ $\lim_{x\rightarrow0}$ $\frac{\frac{1}{2}\sin^{2}x}{3x^{2}}$ $=$ $\frac{\frac{1}{2}}{3}$ $=$ $\frac{1}{6}$
方法一的手写作答:

方法二的手写作答:

EOF
甲乙两人赛跑,计时开始时,甲在乙前方 $10$(单位:m)处. 图中,实线表示甲的速度曲线 $v$ $=$ $v_{1}(t)$ (单位 : m/s),虚线表示乙的速度曲线 $v$ $=$ $v_{2}(t)$ (单位 : m/s),三块阴影部分面积的数值依次为 $10$, $20$, $3$. 计时开始后乙追上甲的时刻记为 $t_{0}$ (单位 : s),则()
( A ) $t_{0}$ $=$ $10$.
( B ) $15$ $<$ $t_{0}$ $<$ $20$.
( C ) $t_{0}$ $=$ $25$.
( D ) $t_{0}$ $>$ $25$.
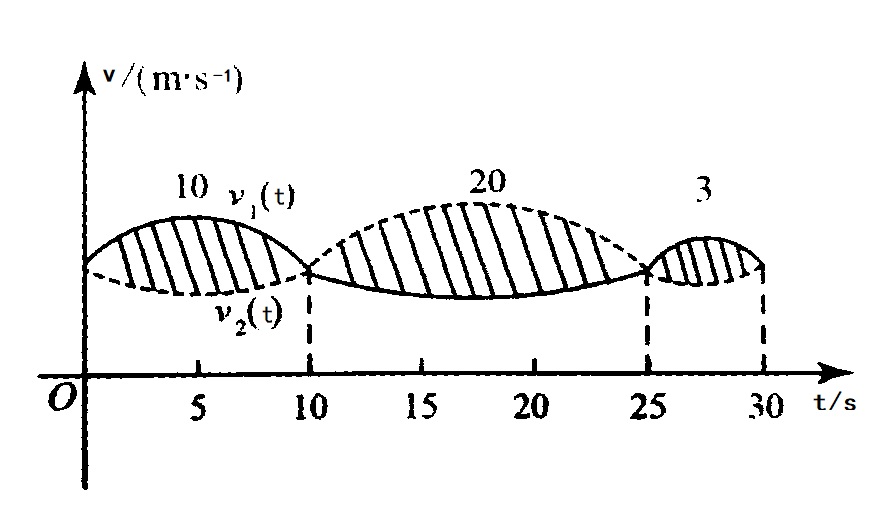
从物理学的角度,本题就是考查速度与路程的关系。
题目中给出的 $X$ $-$ $Y$ 坐标图像是“时间-速度”图像。那么,根据物理学知识我们知道,该曲线与坐标轴围成的图像的面积就是走过的路程。我们又知道,实线表示甲,虚线表示乙,而且刚开始时甲在乙前面 $10$ 米处。
由图像可知,当 $t$ $=$ $10$ 时,甲在乙前面 $20$ 米处,当 $t$ $=$ $25$ 时,乙在第 $10$ 秒到第 $25$ 秒之间的 $15$ 秒时间里比甲多跑了 $20$ 米,正好抵消了之前乙落后于甲的 $20$ 米路程。因此,当 $t$ $=$ $25$ 时,乙追上了甲,即 $t_{0}$ $=$ $25$。
综上可知,本题的正确选项是:$C$.
从数学的角度,本题主要考查的是定积分的基本运算和定积分的几何意义。
使用高等数学解答本题需要如下关于定积分的知识:
$\int_{a}^{b}$ $[$ $k_{1}$ $f_{1}(x)$ $+$ $k_{2}$ $f_{2}(x)$ $]$ $dx$ $=$ $k_{1}$ $\int_{a}^{b}$ $f_{1}(x)$ $dx$ $+$ $k_{2}$ $\int_{a}^{b}$ $f_{2}(x)$ $dx$.
定积分积分区间的可加性:
$\int_{a}^{b}$ $f(x)$ $dx$ $=$ $\int_{a}^{c}$ $f(x)$ $dx$ $+$ $\int_{c}^{b}$ $f(x)$ $dx$.
根据上面的知识,我们可以做如下推理。
如果我们约定,使用 $v(t)$ 表示速度,使用 $s(t)$ 表示路程,那么在从 $0$ 到 $t$ 这个时间段内,可以写出如下定积分表达式:
$s(t)$ $=$ $\int_{0}^{t}$ $v(t)$ $dx$.
因此,当乙在 $t_{0}$ 时刻追上甲时,甲走过的路程为:
$s_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{1}(t)$.
乙走过的路程为:
$s_{2}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{2}(t)$.
$s_{2}(t)$
和 $s_{1}(t)$ 的关系为:
$s_{2}(t)$ $-$ $10$ $=$ $s_{1}(t)$.
于是有:
$s_{2}(t)$ $-$ $s_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $v_{2}(t)$ $-$ $\int_{0}^{t_{0}}$ $v_{1}(t)$ $=$ $\int_{0}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.
由于在从 $0$ 到 $10$ 秒的时间段内,$v_{2}$ 始终大于 $v_{1}$, 因此,乙超过甲的时间 $t_{0}$ 一定大于 $10$, 于是有:
$\int_{0}^{10}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $+$ $\int_{10}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.
又由于,从题中给出的图像我们可以看出:
$\int_{0}^{10}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $10$.
因此有:
$\int_{10}^{t_{0}}$ $[$ $v_{2}(t)$ $-$ $v_{1}(t)$ $]$ $=$ $20$. (1)
根据题中图像可知,在第 $10$ 秒到第 $25$ 秒这段时间里,图像中对应的阴影部分的面积为 $20$, 所以当 $t_{0}$ $=$ $25$ 时, $(1) $ 式成立。
综上可知,本题的正确选项是:$C$.
EOF
已知函数 $f(x)$ $=$ $\frac{1}{1+x^{2}}$, 则 $f^{(3)}(0)$ $=$
本题可以借助函数奇偶性的相关性质解出。
由于:
$f(x)$ $=$ $\frac{1}{1+x^{2}}$
$f(x)$ $=$ $\frac{1}{1+x^{2}}$
$f(-x)$ $=$ $\frac{1}{1+(-x)^{2}}$ $=$ $\frac{1}{1+x^{2}}$
因此:
$f(x)$ $=$ $f(-x)$
于是,我们知道,函数 $f(x)$ 是一个偶函数。
接下来,根据“偶函数的导数是奇函数,奇函数的导数是偶函数”的规律,我们知道,函数 $f^{(3)}(x)$ 是一个奇函数。
又由于,如果一个奇函数 $g(x)$ 在原点处$($ $x$ $=$ $0$ $)$有定义,则 $g(x)$ $=$ $0$, 因此有:
$f^{(3)}(0)$ $=$ $0$
综上可知,本题的答案就是:$0$.
本题也可以借助泰勒级数计算。
本题要求解的是在 $x$ $=$ $0$ 时,$f(x)$ 的三次导函数的函数值。我们知道,麦克劳林级数就是函数在 $x$ $=$ $0$ 处的泰勒级数,是泰勒级数的一个特例。于是,这里我们可以使用麦克劳林级数对原式进行级数展开。
麦克劳林级数中有一个关于几何级数的公式,如下:
$\frac{1}{1-x}$ $=$ $\sum_{0}^{\infty}$ $x^{n}$, $|x|$ $<$ $1$
当我们把上述公式中的 $x$ 替换成 $-x^{2}$ 后,$f(x)$ 就可以使用上述几何级数的公式表达,如下:
$f(x)$ $=$ $\frac{1}{1+x^{2}}$ $=$ $\frac{1}{1-(-x^{2})}$ $=$ $\sum_{0}^{\infty}$ $(-x^{2})^{n}$ $=$ $\sum_{0}^{\infty}$ $(-1)^{n}$ $x^{2n}$
之后,对 $f(x)$ 求导:
$f'(x)$ $=$ $\sum_{0}^{\infty}$ $(-1)^{n}$ $\cdot$ $2n$ $\cdot$ $x^{2n-1}$
$f”(x)$ $=$ $\sum_{0}^{\infty}$ $(-1)^{n}$ $\cdot$ $2n$ $\cdot$ $(2n-1)$ $\cdot$ $x^{2n-2}$
$f”'(x)$ $=$ $\sum_{0}^{\infty}$ $(-1)^{n}$ $\cdot$ $2n$ $\cdot$ $(2n-1)$ $\cdot$ $(2n-2)$ $\cdot$ $x^{2n-3}$
于是,$f”'(0)=0$.
综上可知,本题的答案就是: $0$.
EOF
若函数 $f(x)$ 可导,且 $f(x)$ $f'(x)$ $>$ $0$, 则()
( A ) $f(1)$ $>$ $f(-1)$
( B ) $f(1)$ $<$ $f(-1)$
( C ) $|f(1)|$ $>$ $|f(-1)|$
( D ) $|f(1)|$ $<$ $|f(-1)|$
观察题目我们可以发现,$f(x)$ $f'(x)$ 和下面这个这个公式很像:
$[f(x)$ $\cdot$ $g(x)]’$ $=$ $f'(x)$ $g(x)$ $+$ $f(x)$ $g'(x)$
如果我们令 $g(x)$ $=$ $f(x)$, 则有:
$f'(x)g(x)$ $+$ $f(x)g'(x)$ $=$ $f'(x)f(x)$ $+$ $f(x)f'(x)$ $=$ $f(x)f'(x)$ $+$ $f(x)f'(x)$ $=$ $2f(x)f'(x)$
进一步,我们可以令 $F(x)$ $=$ $f^{2}(x)$, 则有:
$F'(x)$ $=$ $2$ $f(x)f'(x)$
由题可知,$f(x)f'(x)$ $>$ $0$, 于是有 $F'(x)$ $>$ $0$, 即 $F(x)$ 是一个单调递增的函数,由此可得:
$F(1)$ $-$ $F(-1)$ $>$ $0$
即:
$f^{2}(1)$ $-$ $f^{2}(-1)$ $>$ $0$ $\Rightarrow$ $f^{2}(1)$ $>$ $f^{2}(-1)$ $\Rightarrow$ $|f(1)|$ $>$ $|f(-1)|$
综上可知,正确答案为:$C$.
EOF