题目
设 $A>0$, $D$ 是由曲线段 $y=$ $A \sin x$ $(0 \leqslant x \leqslant \frac{\pi}{2})$ 及直线 $y=0$, $x = \frac{\pi}{2}$ 所围成的平面区域，$V_{1}$, $V_{2}$ 分别表示 $D$ 绕 $x$ 轴与绕 $y$ 轴旋转所成旋转体的体积，若 $V_{1}=V_{2}$, 求 $A$ 的值.
继续阅读“2015年考研数二第16题解析：定积分、旋转体的体积”分类： 高等数学
2015年考研数二第15题解析：等价无穷小、麦克劳林公式
题目
设函数 $f(x)=$ $x +$ $a \ln(1+x) +$ $bx \sin x$, $g(x)=$ $kx^{3}$. 若 $f(x)$ 与 $g(x)$ 在 $x \rightarrow 0$ 时是等价无穷小，求 $a$, $b$, $k$ 的值.
继续阅读“2015年考研数二第15题解析：等价无穷小、麦克劳林公式”2014年考研数二第23题解析：矩阵相似性、矩阵相似对角化
题目
证明：$n$ 阶矩阵 $\begin{bmatrix}
1 & 1 & \cdots & 1\\
1 & 1 & \cdots & 1\\
\vdots & \vdots & & \vdots\\
1 & 1 & \cdots & 1
\end{bmatrix}$ 与 $\begin{bmatrix}
0 & \cdots & 0 & 1\\
0 & \cdots & 0 & 2\\
\vdots & & \vdots & \vdots\\
0 & \cdots & 0 & n
\end{bmatrix}$ 相似.
2014年考研数二第21题解析：旋转体的体积、偏导数
题目
已知函数 $f(x,y)$ 满足 $\frac{\partial f}{\partial y} =$ $2(y+1)$, 且 $f(y,y) =$ $(y+1)^{2}-$ $(2-y) \ln y$, 求曲线 $f(x,y)=0$ 所围图形绕直线 $y=-1$ 旋转所成旋转体的体积.
继续阅读“2014年考研数二第21题解析：旋转体的体积、偏导数”2014年考研数二第20题解析：极限、数列、数学归纳法
题目
设函数 $f(x)=$ $\frac{x}{1+x}$, $x \in [0,1]$, 定义数列：
$$
f_{1}(x) = f(x),
$$
$$
f_{2}(x) = f[f_{1}(x)],
$$
$$
\cdot \cdot \cdot,
$$
$$
f_{n}(x) = f[f_{n-1}(x)],
$$
$$
\cdot \cdot \cdot
$$
记 $S_{n}$ 是曲线 $y=f_{n}(x)$, 直线 $x=1$ 及 $x$ 轴所围平面图形的面积，求极限 $\lim_{n \rightarrow \infty} n S_{n}$.
继续阅读“2014年考研数二第20题解析：极限、数列、数学归纳法”2014年考研数二第19题解析：变上限积分、函数的单调性、积分中值定理
题目
设 $f(x)$, $g(x)$ 在 $[a,b]$ 上连续，且 $f(x)$ 单调增加，$0 \leqslant g(x) \leqslant 1$, 证明：
$(Ⅰ)$ $0 \leqslant \int_{a}^{x} g(t) dt$ $\leqslant x-a$, $x \in [a,b]$;
$(Ⅱ)$ $\int_{a}^{a+\int_{a}^{b}g(t) dt} f(x) dx$ $\leqslant$ $\int_{a}^{b} f(x) g(x) dx$.
继续阅读“2014年考研数二第19题解析：变上限积分、函数的单调性、积分中值定理”2014年考研数二第18题解析：偏导数、二阶常系数非齐次线性微分方程
题目
设函数 $f(u)$ 二阶连续可导，$z=f(e^{x} \cos y)$ 满足 $\frac{\partial ^{2} z}{\partial x^{2}} + \frac{\partial ^{2} z}{\partial y^{2}}$ $=(4z + e^{x} \cos y)e^{2x}$, 若 $f(0)=0$, $f^{‘}(0)=0$, 求 $f(u)$ 的表达式.
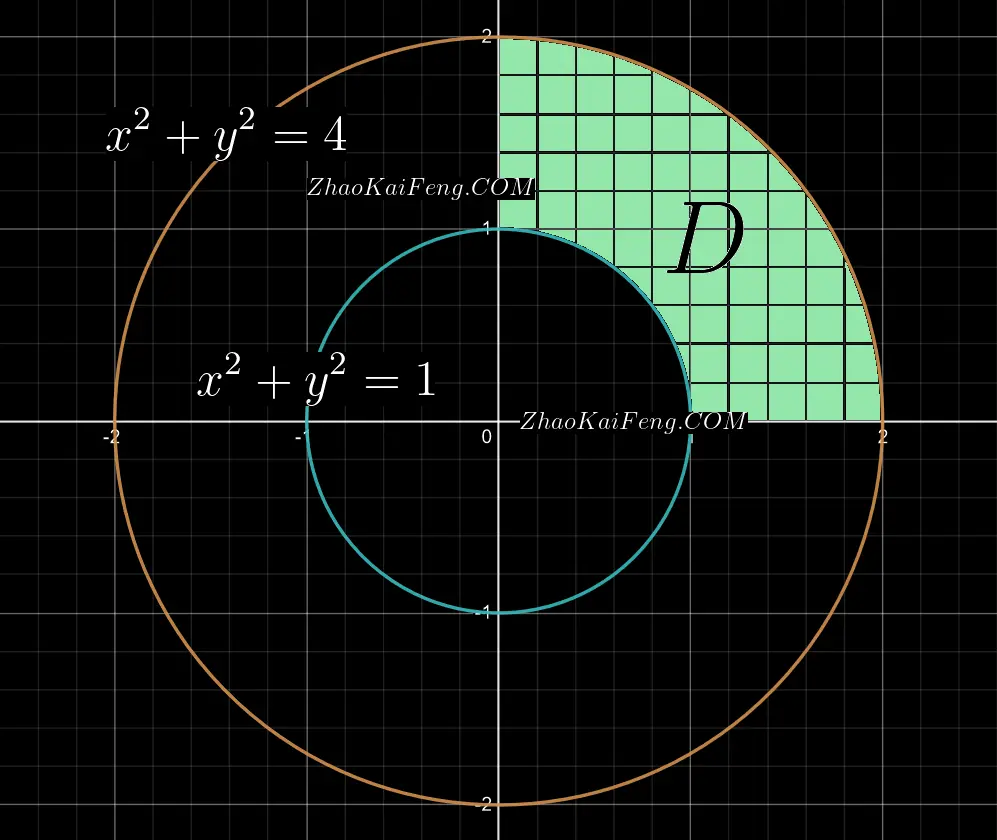
继续阅读“2014年考研数二第18题解析：偏导数、二阶常系数非齐次线性微分方程”2014年考研数二第17题解析：二重积分、极坐标系
题目
设平面区域 $D=$ $\{(x,y)|$ $1 \leqslant x^{2} + y^{2} \leqslant 4$, $x \geqslant 0$, $y \geqslant 0 \}$, 计算：
$$
\iint_{D} \frac{x \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} dxdy.
$$
解析
根据题目可知，积分区域 $D$ 是由两个圆心坐标均为 $(0,0)$, 半径分别为 $1$ 和 $2$ 的两个同心圆在直角坐标系的第一象限中围成的，如图 01 所示：
2014年考研数二第16题解析：一阶线性微分方程求极值、求导
题目
已知函数 $y=y(x)$ 满足微分方程 $x^{2}+y^{2}y^{‘} = 1-y^{‘}$, 且 $y(2)=0$, 求 $y=y(x)$ 的极大值与极小值.
继续阅读“2014年考研数二第16题解析：一阶线性微分方程求极值、求导”2014年考研数二第15题解析：极限、等价无穷小、麦克劳林公式
题目
求极限：
$$
\lim_{x \rightarrow + \infty} \frac{ \int_{1}^{x}[t^{2}(e^{\frac{1}{t}}-1)-t] dt }{x^{2} \ln (1+\frac{1}{x})}.
$$
2013年考研数二第21题解析：平面曲线的弧长、平面图形的形心
题目
设曲线 $L$ 的方程为 $y=\frac{1}{4} x^{2} – \frac{1}{2} \ln x$ $(1 \leqslant x \leqslant e)$.
$(Ⅰ)$ 求 $L$ 的弧长；
$(Ⅱ)$ 设 $D$ 是由曲线 $L$, 直线 $x=1$, $x=e$ 及 $x$ 轴所围平面图形，求 $D$ 的形心的横坐标.
继续阅读“2013年考研数二第21题解析：平面曲线的弧长、平面图形的形心”$x \ln x$的原函数是多少？
$x \ln x$ 的原函数是 $\frac{1}{2} x^{2} \ln x – \frac{1}{4} x^{2} + C$, 即：
$$
\int x \ln x dx = \frac{1}{2} x^{2} \ln x – \frac{1}{4} x^{2} + C, 其中 C 为任意常数。
$$
$\ln x$的原函数是多少？
$\ln x$ 的原函数是 $x \ln x – x + C$, 即：
$$
\int \ln x dx = x \ln x – x + C, 其中 C 为任意常数。
$$
2013年考研数二第20题解析：导数与最值、数列极限的判定与求解
题目
设函数 $f(x)=\ln x + \frac{1}{x}$.
$(Ⅰ)$ 求 $f(x)$ 的最小值；
$(Ⅱ)$ 设数列 ${x_{n}}$ 满足 $\ln x_{n} + \frac{1}{x_{n+1}}<1$. 证明 $\lim_{n \rightarrow \infty} x_{n}$ 存在，并求此极限。
继续阅读“2013年考研数二第20题解析：导数与最值、数列极限的判定与求解”2013年考研数二第19题解析：拉格朗日乘数法求条件极值、求曲线上的最值
题目
求曲线 $x^{3}-xy+y^{3}=1$ $(x \geqslant 0, y \geqslant 0)$ 上的点到坐标原点的最长距离与最短距离。
继续阅读“2013年考研数二第19题解析：拉格朗日乘数法求条件极值、求曲线上的最值”