题目
已知函数 $f(x) =$ $\int_{x}^{1} \sqrt{1+t^{2}} {\rm d} t +$ $\int_{1}^{x^{2}} \sqrt{1+t} {\rm d} t$, 求 $f(x)$ 零点的个数.
解析
首先要明确一点,函数 $f(x)$ 的零点,就是使 $f(x) = 0$ 成立的点。
根据题目,有:
$$
f^{‘}(x) =
$$
$$
(-1) \cdot \sqrt{1+x^{2}} + 2x \sqrt{1+x^{2}} =
$$
$$
(2x-1) \sqrt{1+x^{2}}.
$$
令 $f^{‘}(x) = 0$, 则:
$$
(2x-1) \sqrt{1+x^{2}} = 0 \Rightarrow
$$
$$
x = \frac{1}{2}.
$$
当 $x < \frac{1}{2}$ 时:
$$
(2x-1) \sqrt{1+x^{2}} < 0 \Rightarrow
$$
$$
f^{‘}(x) < 0.
$$
当 $x > \frac{1}{2}$ 时:
$$
(2x-1) \sqrt{1+x^{2}} > 0 \Rightarrow
$$
$$
f^{‘}(x) > 0.
$$
综上可知:
- 函数 $f(x)$ 在区间 $(- \infty, \frac{1}{2})$ 上单调递减;
- 函数 $f(x)$ 在区间 $(\frac{1}{2}, + \infty)$ 上单调递增。
于是,当 $x = \frac{1}{2}$ 时,函数 $f(x)$ 取得最小值,且:
$$
f(\frac{1}{2}) =
$$
$$
\int_{\frac{1}{2}}^{1} \sqrt{1+t^{2}} {\rm d} t + \int_{1}^{\frac{1}{4}} \sqrt{1+t} {\rm d} t =
$$
$$
\int_{\frac{1}{2}}^{1} \sqrt{1+t^{2}} {\rm d} t – \int_{\frac{1}{4}}^{1} \sqrt{1+t} {\rm d} t.
$$
分析可知,$\int_{\frac{1}{2}}^{1} \sqrt{1+t^{2}} {\rm d} t$ 的积分区间 $[\frac{1}{2}, 1]$ 只是 $\int_{\frac{1}{4}}^{1} \sqrt{1+t} {\rm d} t$ 的积分区间 $[\frac{1}{4}, 1]$ 的一个子集,而且,在区间 $(0,1]$ 中,必有 $t^{2} < t$, 于是:
$$
\int_{\frac{1}{2}}^{1} \sqrt{1+t^{2}} {\rm d} t < \int_{\frac{1}{4}}^{1} \sqrt{1+t} {\rm d} t \Rightarrow
$$
$$
\int_{\frac{1}{2}}^{1} \sqrt{1+t^{2}} {\rm d} t – \int_{\frac{1}{4}}^{1} \sqrt{1+t} {\rm d} t < 0 \Rightarrow
$$
$$
f(\frac{1}{2}) < 0.
$$
注:
[1]. 计算可知:
$\int_{\frac{1}{2}}^{1} \sqrt{1+t^{2}} {\rm d} t \approx 0.627679164979$;
$\int_{\frac{1}{4}}^{1} \sqrt{1+t} {\rm d} t \approx 0.953923092539$.
又由于 $\sqrt{1+t^{2}} > 0$ 和 $\sqrt{1+t} > 0$ 始终成立,因此:
$$
\lim_{x \rightarrow – \infty} f(x) > 0;
$$
$$
\lim_{x \rightarrow + \infty} f(x) > 0.
$$
因此,函数 $f(x)$ 有两个零点:
- 函数 $f(x)$ 在区间 $(-\infty, \frac{1}{2})$ 之间存在一个零点;
- 函数 $f(x)$ 在区间 $(\frac{1}{2}, +\infty)$ 之间存在一个零点。由于 $f(1) =$ $\int_{1}^{1} \sqrt{1+t^{2}} {\rm d} t +$ $\int_{1}^{1} \sqrt{1+t} {\rm d} t =$ $0+0=0$, 所以,位于区间 $(\frac{1}{2}, +\infty)$ 上的这个零点就是点 $(1,0)$.
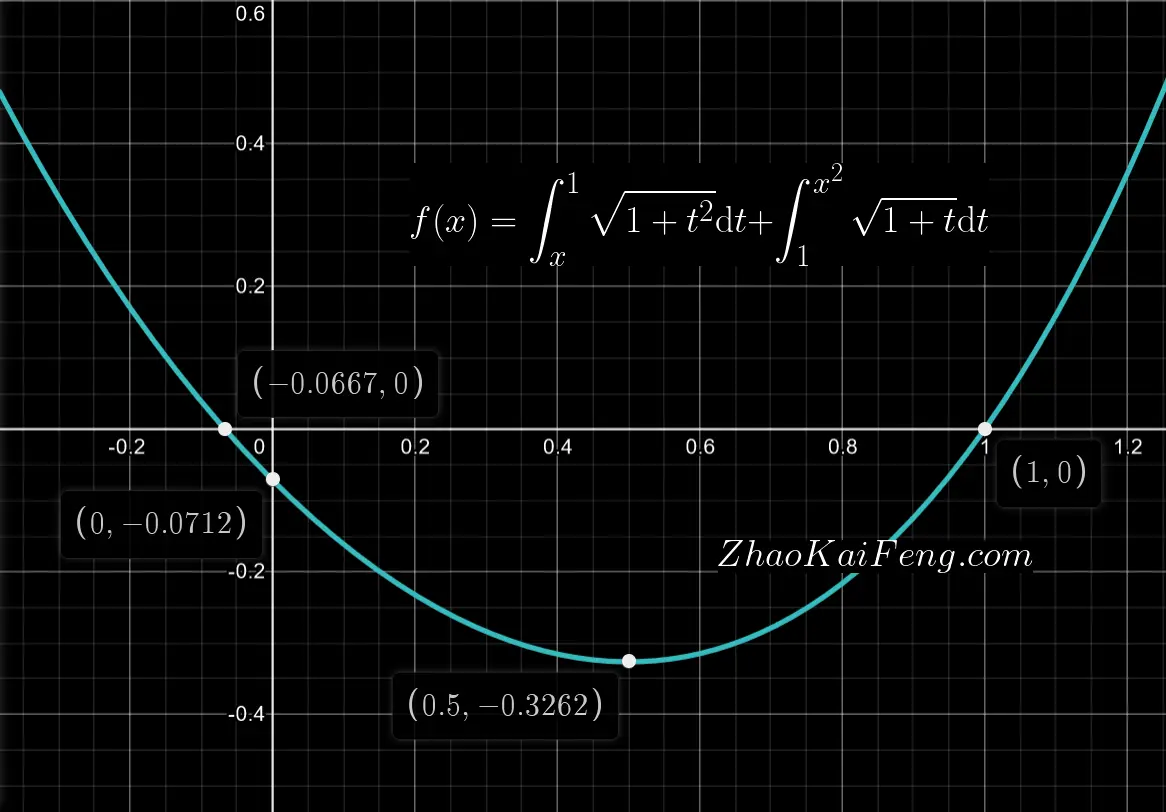
补充
函数 $f(x) =$ $\int_{x}^{1} \sqrt{1+t^{2}} {\rm d} t +$ $\int_{1}^{x^{2}} \sqrt{1+t} {\rm d} t$ 的具体图像可以参考图 01: