先来看一下互斥事件与对立事件的定义。
互斥事件的定义:
互斥事件(互不相容):当 $AB$ $=$ $\varnothing$ (也可以写成 $A$ $\cap$ $B$ $=$ $\varnothing$)时,称事件 $A$ 与 事件$B$ 互不相容或互斥,事件 $A$, $B$ 不能同时发生.
对立事件的定义:
对立事件(逆事件):若 $A$ $\cup$ $B$ $=$ $\Omega$ 且 $A$ $\cap$ $B$ $=$ $\varnothing$, 则称 $A$ 与 $B$ 互为逆事件,也称互为对立事件. $A$ 的对立事件记为 $\bar{A}$.
总的来说,互斥事件是一个比对立事件更广泛一些的概念,这一点从互斥事件与对立事件各自的定义上也可以看出来。互斥事件只限制了 $A$ $\cap$ $B$ $=$ $\varnothing$, 而对立事件不仅限制了 $A$ $\cap$ $B$ $=$ $\varnothing$, 还限制了 $A$ $\cup$ $B$ $=$ $\Omega$. 很显然,互斥事件的限制范围更宽松,因此能表示的范围也更大。
我们可以将互斥事件和对立事件理解成包含和被包含的关系:
对立必然互斥,互斥不一定对立。
如果要用普通语言表述互斥事件与对立事件,那就是:
对立是要么一定且只能是我,要么就一定且只能是你;
互斥是如果不是我,则可能是你,也可能另外的其他人。
为了进一步辅助理解,我画了两张图,大致表示出了对立事件和互斥事件,如下。
图 1 表示 $A$ 与 $B$ 为对立事件时其相互之间的关系:
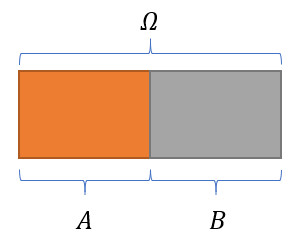
图 2 表示 $A$ 与 $B$ 为互斥事件时其 相互之间的关系:
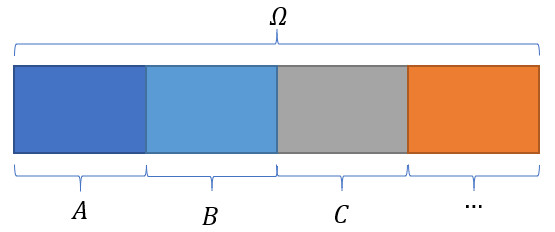
注:本文中的 “$\Omega$” 表示当前语境下的样本空间,即当前语境下所有样本点组成的集合。
高等数学
涵盖高等数学基础概念、解题技巧等内容,图文并茂,计算过程清晰严谨。
线性代数
以独特的视角解析线性代数,让繁复的知识变得直观明了。
特别专题
通过专题的形式对数学知识结构做必要的补充,使所学知识更加连贯坚实。
EOF