通过二阶导函数和一阶导函数的函数图像判断原函数拐点的个数

总结：拐点本质上是二阶导的正负性发生改变的点，这个点可能是二阶导等于零的点，也可能是二阶导不存在的点。

题目 01

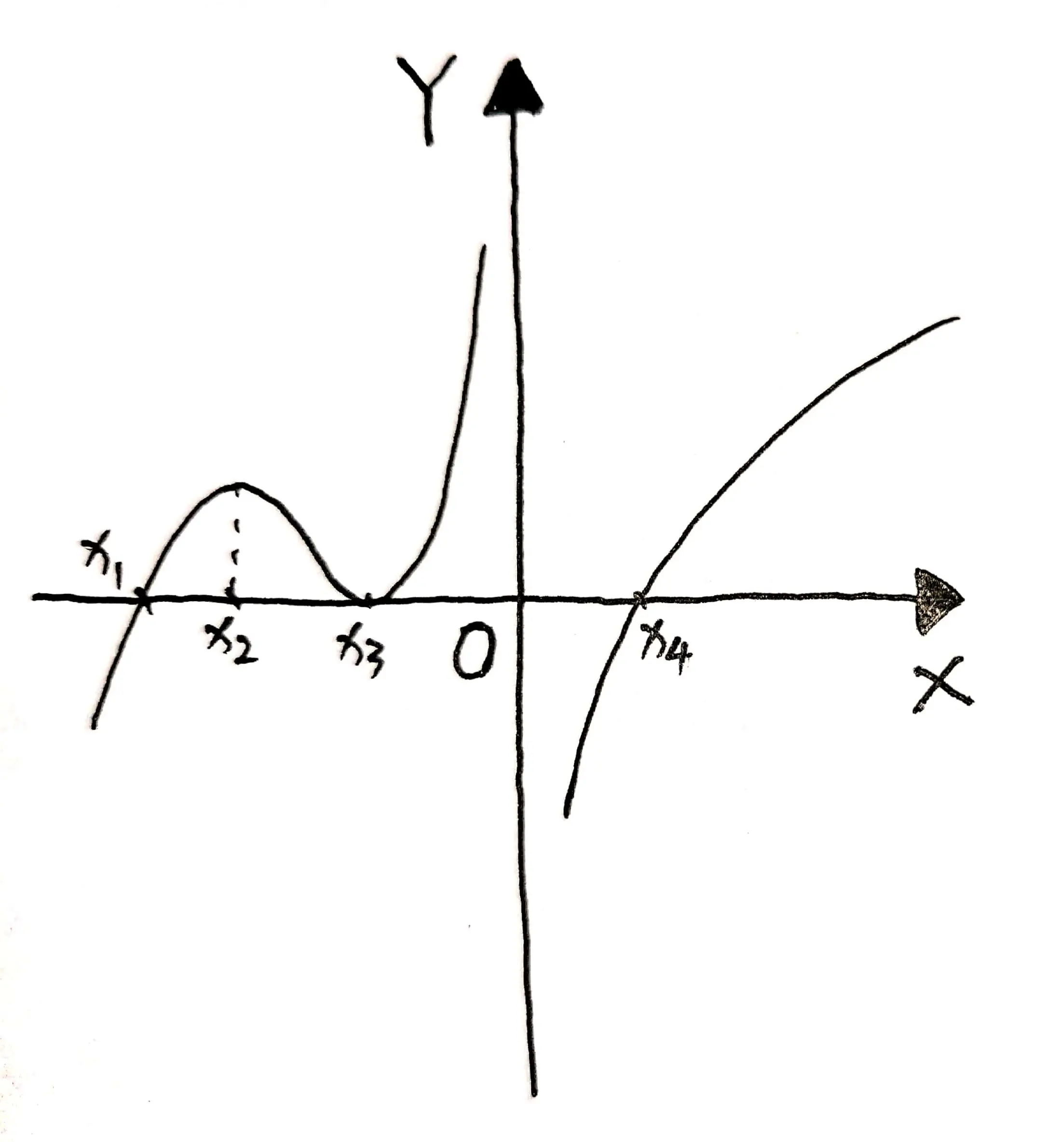
已知，函数 $y=f(x)$ 在 $(-\infty,+\infty)$ 连续，其二阶导函数的图形如图 01 所示，则 $y=f(x)$ 的拐点的个数是多少？

难度评级：

解析 01

由于二阶导正负发生改变的点就是拐点，因此，据图可知，以下三个点是拐点：

$$
\begin{cases}
x = x_{1} \\
\textcolor{orangered}{ x = 0 } \\
x = x_{4}
\end{cases}
$$

另一种判断方法：二阶导等于零且左右两侧异号的点 $x = x_{1}$, $x = x_{4}$ 一定是拐点、二阶导不存在的点 $x = 0$ 左右两侧也正负异号，因此同样是拐点。

注意：二阶导等于零和二阶导不存在的点都不一定是拐点

Next

题目 02

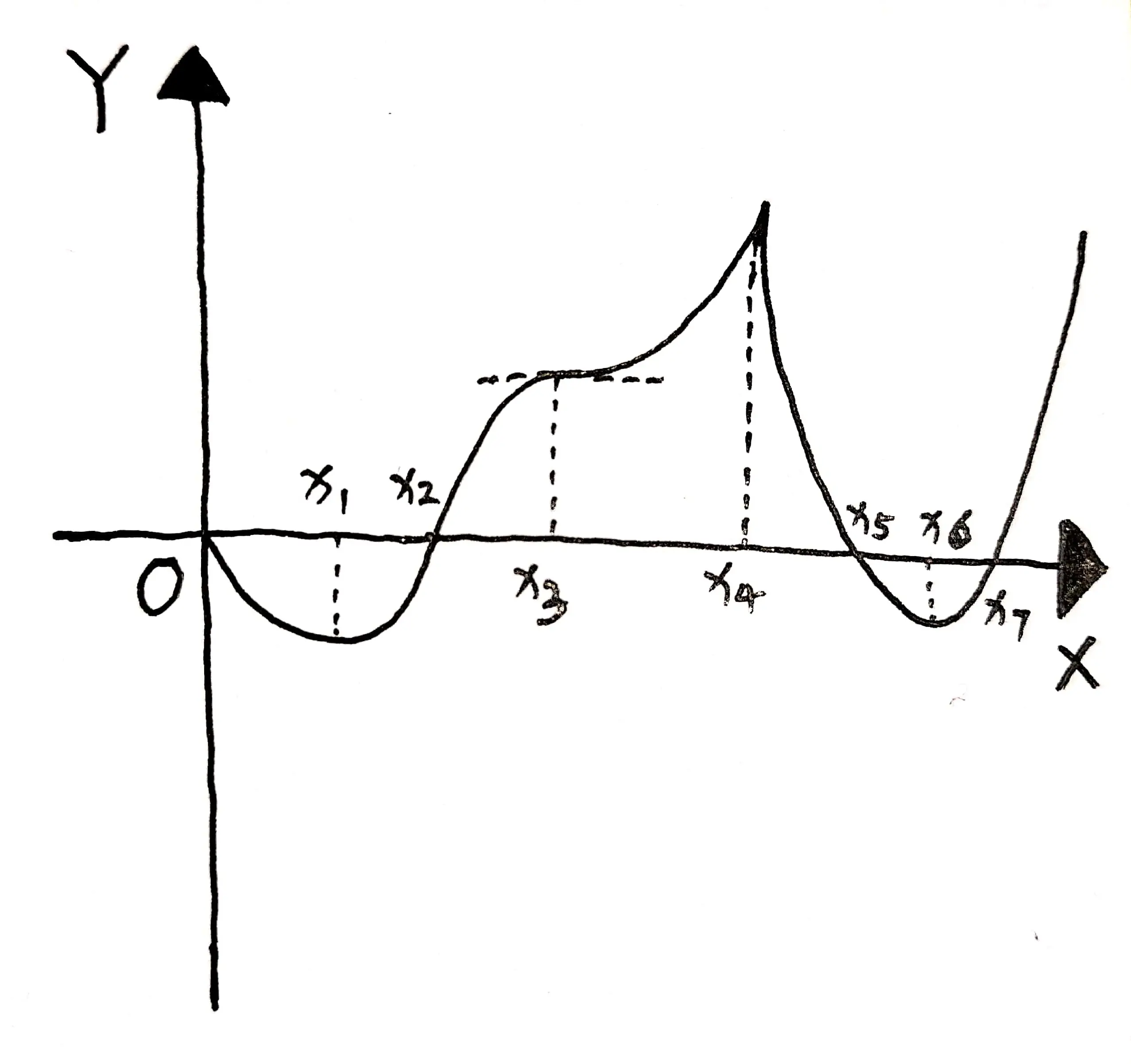
已知，在 $[0,+\infty)$ 区间上 $y=f(x)$ 的导函数的图形如下图 02 所示，则 $y=f(x)$ 的拐点的个数是多少？

难度评级：

解析 02

二阶导等于零的点（一阶导的驻点，即原函数切线水平的点）可能是拐点：

$$
\begin{cases}
x = x_{1} \\
x = x_{3} \\
x = x_{6}
\end{cases}
$$

二阶导不存在（一阶导不可导）的点也可能是拐点：

$$
x = x_{4}
$$

继续分许可知：

$x = x_{1}$ 和 $x = x_{6}$ 两侧单调性相反，继续求导得到的原函数的二阶导函数一定正负异号，所以这两个点一定是原函数的拐点，同理可知，$x = x_{3}$ 的左右两侧单调性不变，因此不是原函数的拐点。

$x = x_{4}$ 处虽然不可导，但单调性同样发生了改变，因此也是原函数的拐点。

---