前言
一般情况下,对于下面这些量是无穷大量,我们应该是没有疑问的:
$$
\begin{aligned}
& \lim_{ x \rightarrow 0^{+} } \ln x & \rightarrow \infty \\ \\
& \lim_{ x \rightarrow 0^{+} } \frac{1}{x} & \rightarrow \infty \\ \\
& \lim_{ x \rightarrow + \infty } x & \rightarrow \infty \\ \\
& \lim_{ x \rightarrow + \infty } \ln x & \rightarrow \infty \\ \\
& \lim_{ x \rightarrow + \infty } x^{2} & \rightarrow \infty \\ \\
& \lim_{ x \rightarrow + \infty } e^{x} & \rightarrow \infty
\end{aligned}
$$
但是,对于下面这些量是否是无穷大量,我们可能会有一些疑问,在本文中,荒原之梦考研数学将帮助大家解决这些疑问:
$$
\begin{aligned}
& \lim_{ x \rightarrow 0 } \left( \frac{1}{x^{2}} \sin \frac{1}{x} \right) & \rightarrow ? \\ \\
& \lim_{n \rightarrow \infty} (-1)^{n} (\sqrt{n}) & \rightarrow ?
\end{aligned}
$$
正文
我们知道,震荡无极限可以分为有界震荡无极限和无界震荡无极限。虽然无穷大量不是极限值,但是一般情况,“震荡”就意味着“不存在”无穷大,或者说不【趋于】无穷大——
这是因为,说一个量是无穷大量,必须要满足的首要条件就是,在某个位置之后,所有的数值都是非常非常大的数字,不能出现常数。
对于 $\frac{1}{x^{2}} \sin \frac{1}{x}$, 当 $x \rightarrow 0$ 的时候,$\frac{1}{x^{2}}$ 会趋于无穷大,但是,$\sin \frac{1}{x}$ 则会在 $-1$ 到 $0$ 以及 $0$ 到 $1$ 之间不断做有界震荡,因此,$\frac{1}{x^{2}} \sin \frac{1}{x}$ 的取值除了会有产生无穷大的情况,也会存在等于 $0$ 的情况(零乘以无穷大仍得零)。
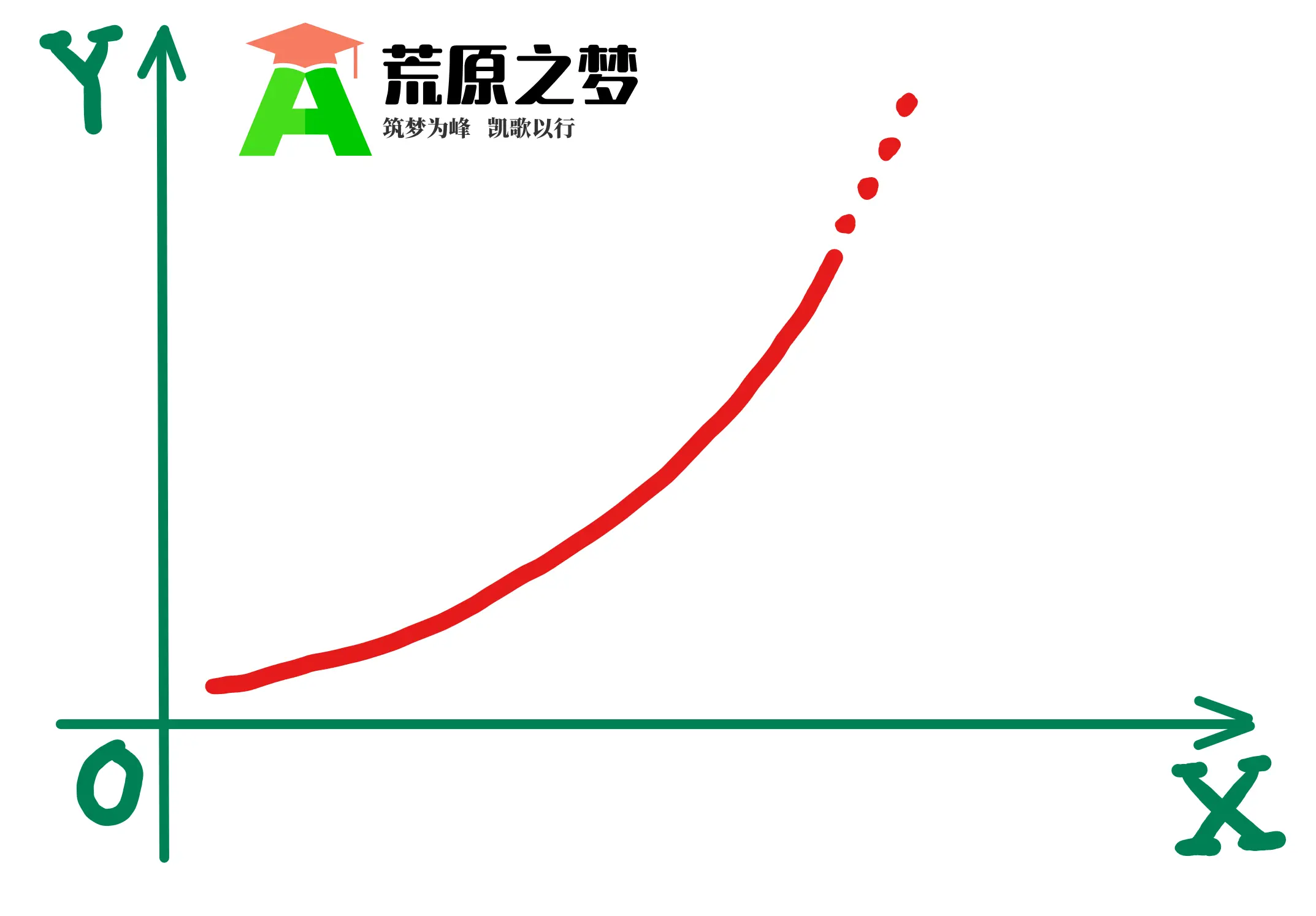
因此,当 $x \rightarrow 0$ 的时候,$\frac{1}{x^{2}} \sin \frac{1}{x}$ 其实是无界震荡且非无穷大量,其函数图像如图 01 所示:
既然取值中有常数(非无穷大量)就不算无穷大量,那么,如果取值只在趋于正无穷和趋于负无穷两个方向上进行,又是否算是无穷大量呢?
虽然说,无论正无穷大还是负无穷大都可以称为“无穷大”,但上面一段所说的这种情况,也不能算是无穷大量。
因为无穷大事实上是要“趋于”的,而“趋于”就意味着在整个过程中,取值的“总体方向”不能发生变化,只能有一个“方向”——
“方向唯一且不能发生变化”不仅要求取值方向上不能出现常数,也要求不能出现相反方向的无穷大量。
例如,对于数列 $\{x_{n} \}$ $=$ $(-1)^{n} (\sqrt{n})$, 当 $n$ $=$ $1$, $2$, $3$. $\cdots$ 时,$x_{n}$ 的取值为:
$$
x_{n} = 1, \quad \sqrt{2}, \quad – \sqrt{3}, \quad \sqrt{4}, \quad – \sqrt{5}, \quad \cdots
$$
从上面的式子,我们可以看出,数列 $\{ x_{n} \}$ 的取值其实是在两个方向上反复变化的,一个方向上趋于 $+ \infty$, 另一个方向上趋于 $- \infty$, 此时,我们只能说数列 $\{ x_{n} \}$ 是一个无界数列,而不能说当 $x \rightarrow \infty$ 时,数列 $\{ x_{n} \}$ 是一个无穷大量。
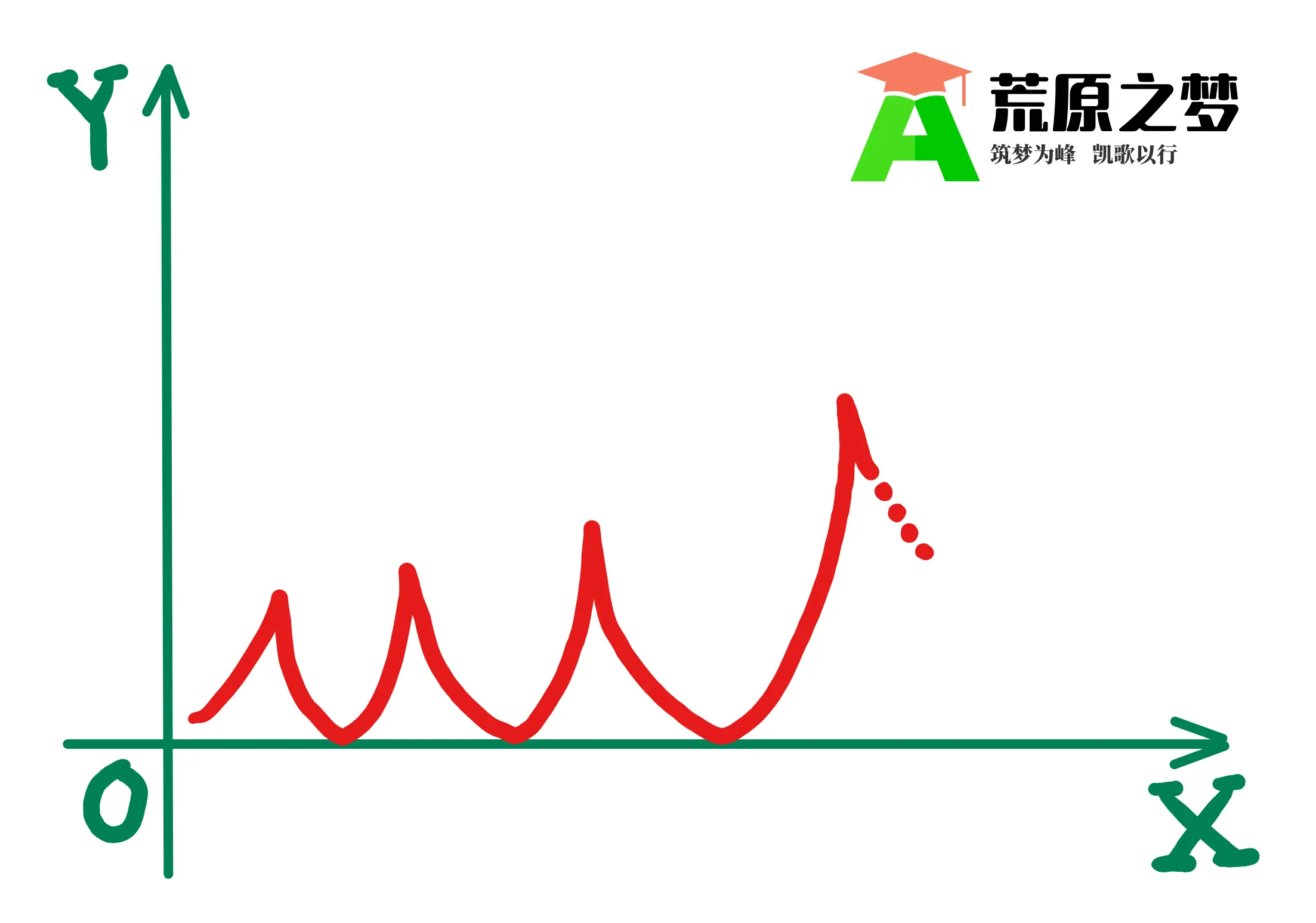
数列 $\{ x_{n} \}$ 的取值示意图如图 02 所示:
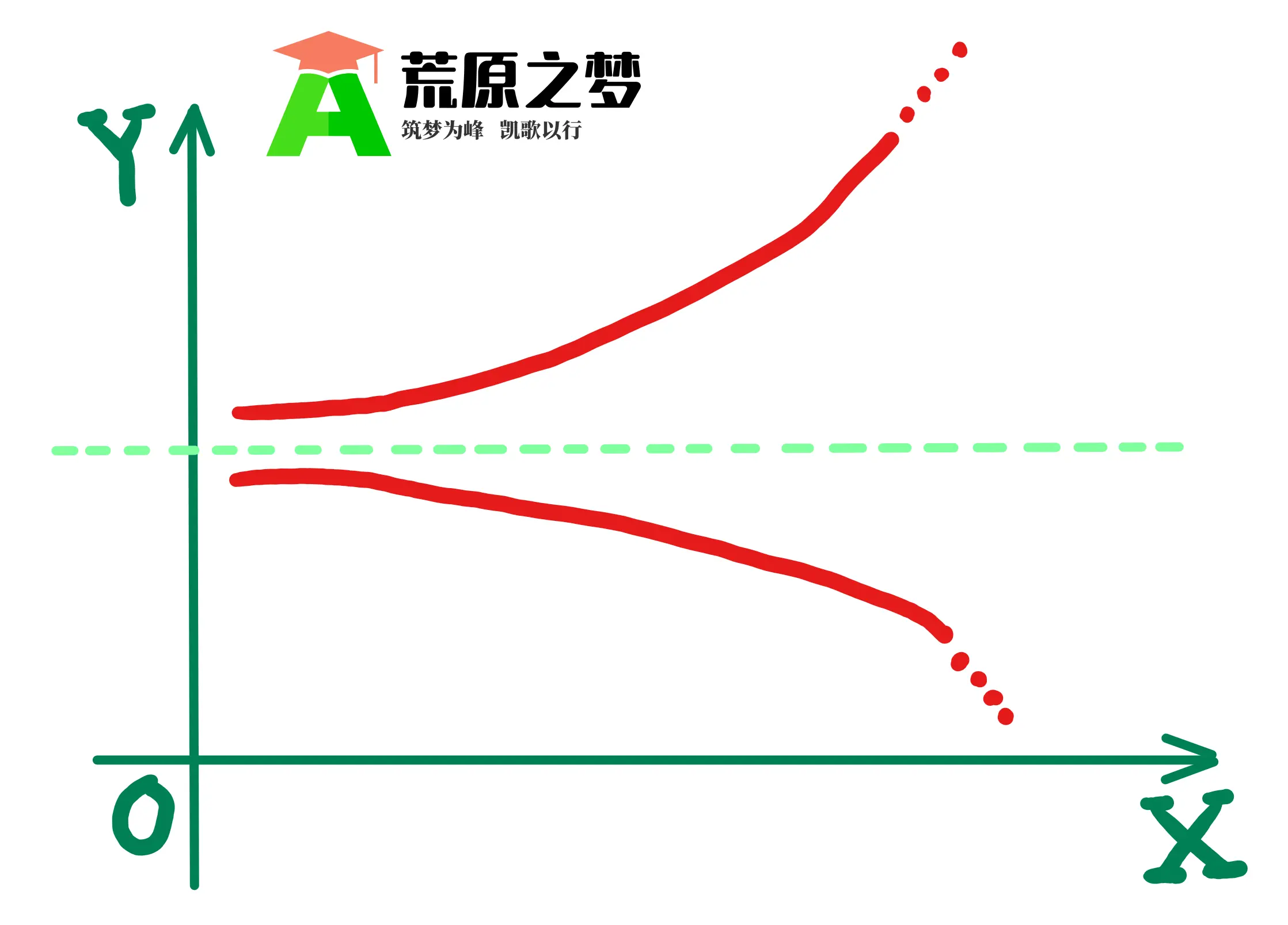
如果要用图示的方式阐明荒原之梦考研数学的这篇笔记,那就是,只有如图 02 的这种形式算是趋向于无穷大量,而如图 03 和如图 04 所示的形式都不能算是趋向于无穷大量:
总结
总的来说,如果要趋于无穷大,就必须保证无穷大趋于路径的唯一性和单向性。由于无论是“震荡”(如上图 02)。还是同时趋于正无穷和负无穷(如上图 03),都破坏了趋于无穷大路径的唯一性和单向性,因此,下面这两个式子都不趋于无穷大:
$$
\begin{aligned}
& \lim_{ x \rightarrow 0 } \left( \frac{1}{x^{2}} \sin \frac{1}{x} \right) & \nRightarrow \infty \\ \\
& \lim_{n \rightarrow \infty} (-1)^{n} (\sqrt{n}) & \nRightarrow \infty
\end{aligned}
$$
高等数学
涵盖高等数学基础概念、解题技巧等内容,图文并茂,计算过程清晰严谨。
线性代数
以独特的视角解析线性代数,让繁复的知识变得直观明了。
特别专题
通过专题的形式对数学知识结构做必要的补充,使所学知识更加连贯坚实。