这道题算是算不出来的，只能“分类讨论”这样子

一、题目

已知 $f(x)$ 在 $[a, b]$ 上可导, 又 $f^{\prime}(x)+f^{2}(x)$ $-$ $\int_{a}^{x} f(t) \mathrm{d} t$ $=$ $0$ 且 $\int_{a}^{b} f(t) \mathrm{d} t=0$, 则 $\int_{a}^{x} f(t) \mathrm{d} t$ 在 $(a, b)$ 内是恒为负？还是恒为正？变号？还是恒为零？

难度评级：

二、解析

若令 $F(x)=\int_{a}^{x} f(t) \mathrm{~ d} t$, 则：

$$
F(a)=\int_{a}^{a} f(t) \mathrm{~ d} t=0
$$

$$
F(b)=\int_{a_{2}}^{b} f(t) \mathrm{~ d} t=0
$$

于是：

$$
f^{\prime}(x)+f^{2}(x)-\int_{a_{2}}^{x} f(t) \mathrm{~ d} t=0 \Rightarrow
$$

$$
F^{\prime \prime}(x)+\left[F^{\prime}(x)\right]^{2}-F(x)=0
$$

接着进行分类讨论：

情况 (1)

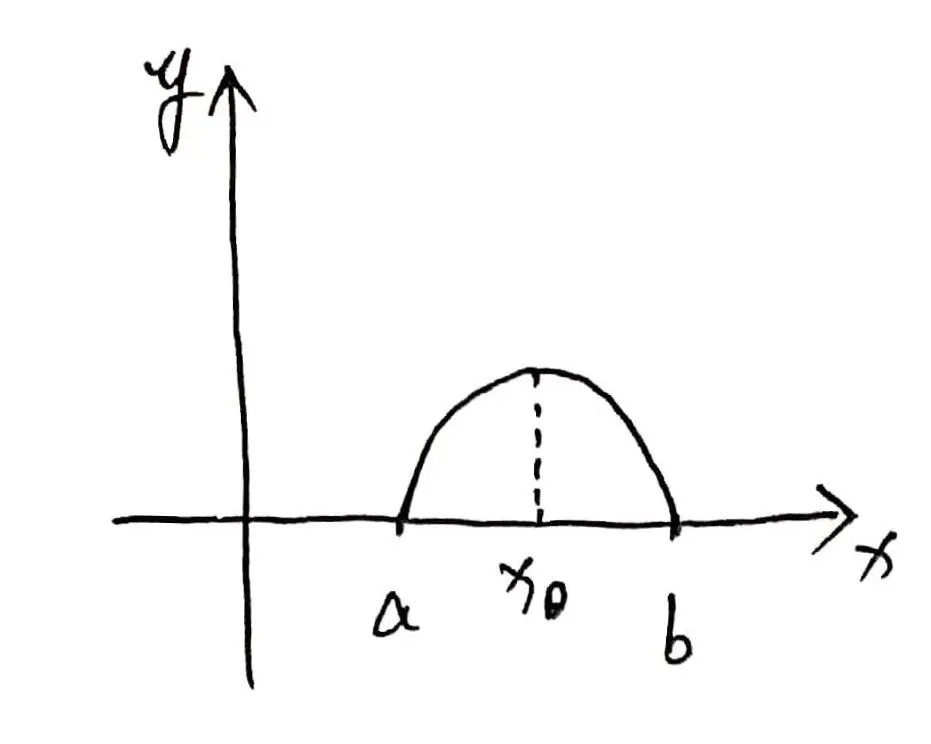
示意图：

$$
x \in[a, b], f(x)>0 \Rightarrow \max [a, b]=x_{0} \Rightarrow
$$

$$
F\left(x_{0}\right)>0, F^{\prime}\left(x_{0}\right)=0, F^{\prime \prime}\left(x_{0}\right) \leqslant 0 \Rightarrow
$$

$$
F^{\prime \prime}\left(x_{0}\right)+\left[F^{\prime}\left(x_{0}\right)\right]^{2}-F\left(x_{0}\right) \Rightarrow
$$

$$
F^{\prime \prime}\left(x_{0}\right)-F\left(x_{0}\right)<0 \neq 0
$$

情况 (2)

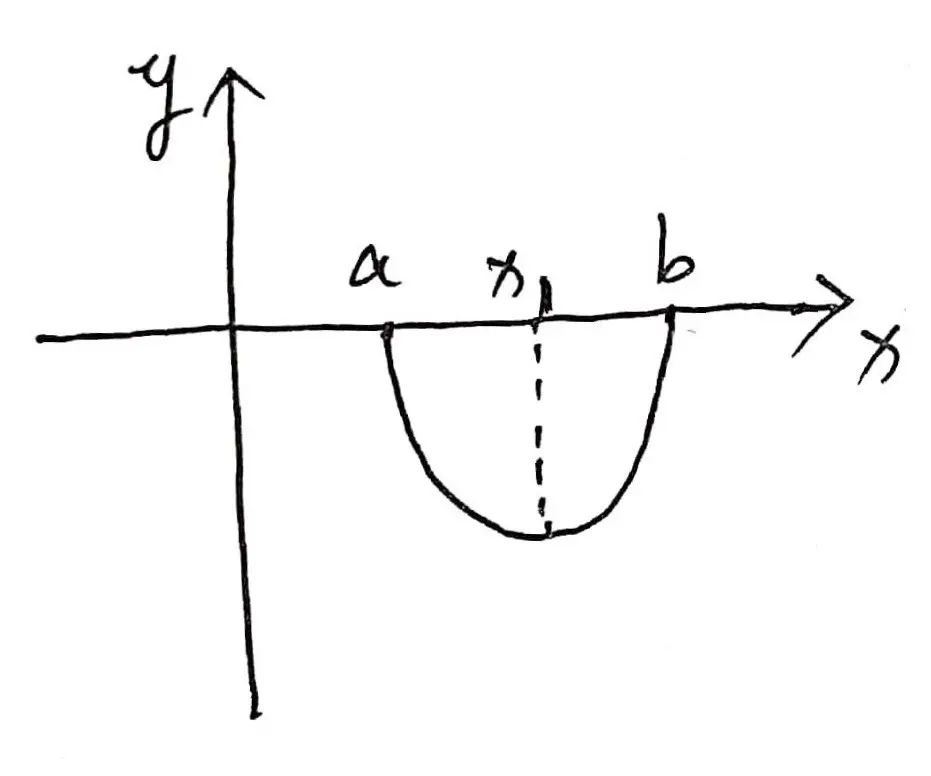
示意图：

$$
x \in[a, b], \quad F(x)<0 \Rightarrow \min [a, b]=x_{1} \Rightarrow
$$

$$
F\left(x_{1}\right)<0, \quad F^{\prime}\left(x_{1}\right)=0, \quad F^{\prime \prime}\left(x_{1}\right) \geqslant 0 \Rightarrow
$$

$$
F^{\prime \prime}\left(x_{1}\right)+\left[F^{\prime}\left(x_{1}\right)\right]^{2}-F\left(x_{1}\right) \Rightarrow
$$

$$
F^{\prime \prime}\left(x_{1}\right)-F\left(x_{1}\right)<0 \neq 0
$$

情况 (3)

$$
x \in[a, c), F(x)>0 \quad x \in[c, b], F(x)<0
$$

示意图：

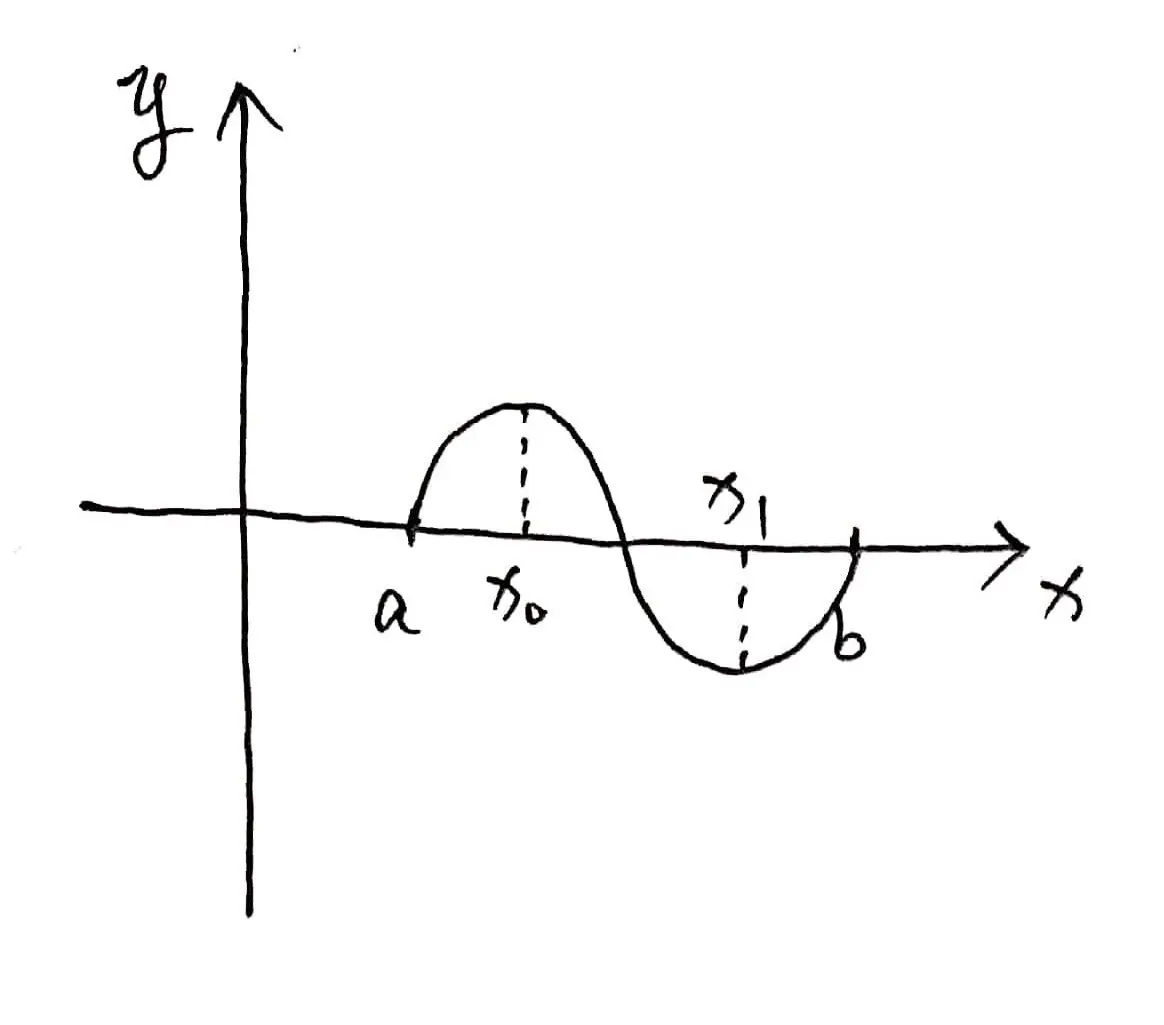
使用类似情况 (1) 和 (2) 中的判断方式可知，$[a, c)$ 和 $[c, d]$ 区间上都不满足 $f^{\prime}(x)+f^{2}(x)$ $-$ $\int_{a}^{x} f(t) \mathrm{d} t$ $=$ $0$

情况 (4)

$$
x \in[a, c), F(x)<0 \quad x \in[c, b], F(x)>0
$$

示意图：

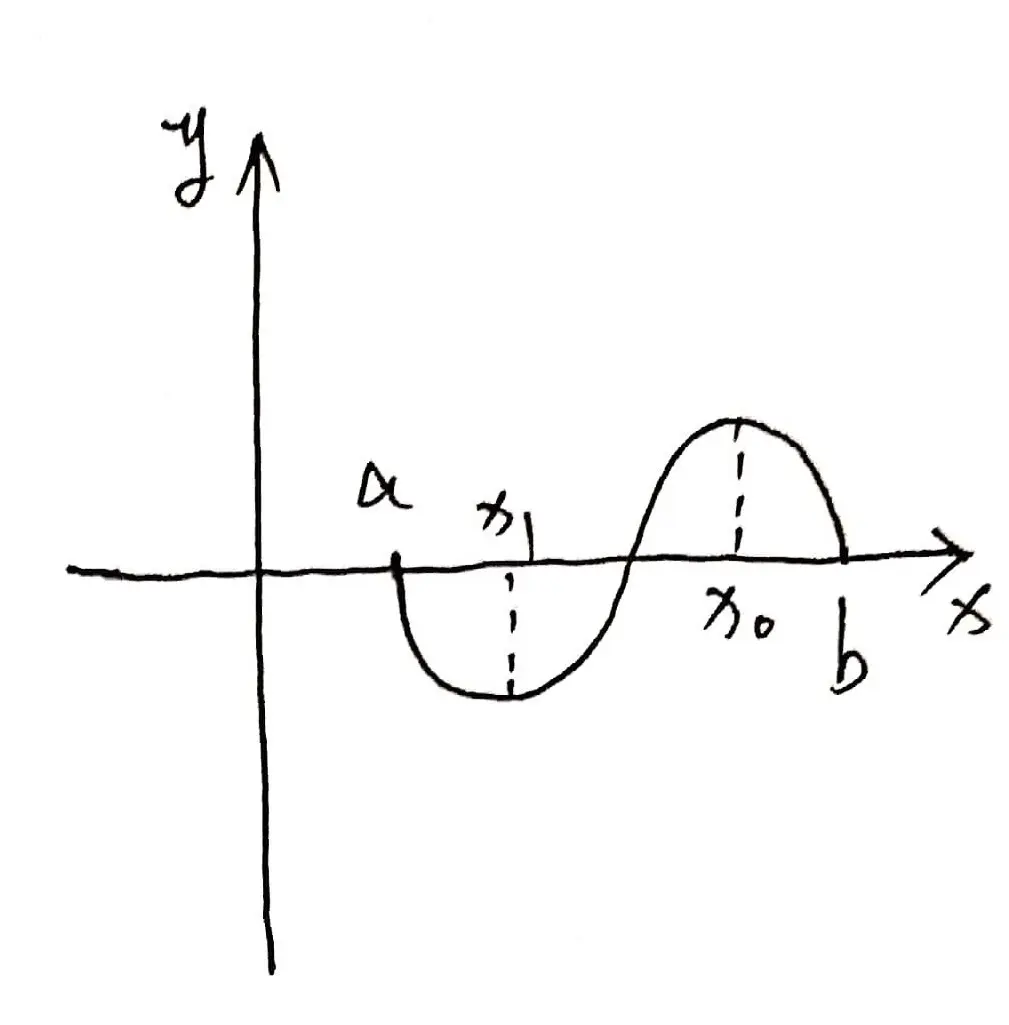
使用类似情况 (1) 和 (2) 中的判断方式可知，$[a, c)$ 和 $[c, d]$ 区间上都不满足 $f^{\prime}(x)+f^{2}(x)$ $-$ $\int_{a}^{x} f(t) \mathrm{d} t$ $=$ $0$

---