明白了这两张图你就记住了这两个重要的常用不等式

一、前言

我们知道，下面这两个不等式很常用也很重要（已知 $a \geqslant 0$, $b \geqslant 0$）：

$$
a^{2} + b^{2} \geqslant 2ab
$$

$$
a + b \geqslant 2 \sqrt{ab}
$$

那么，你知道这两个不等式背后隐藏的几何规律吗？你是怎么记住这两个不等式的？其实，只要搞明白这背后的几何原理，想记不住它们都难哦！

Tips:

本文中的理解方法由荒原之梦（zhaokaifeng.com）原创。

二、解析

$a^{2} + b^{2} \geqslant 2ab$ $\Rightarrow$ $a^{2} + b^{2} \geqslant ab + ab$

该不等式表达的意思就是：

在【和】一定的情况下，两个数字越【接近】，相【乘】所得的数就越【大】。

例如，$2 + 2$ 和 $1 + 3$ 都等于 $4$, 但是，由于 $2$ 和 $2$ 很“接近”，$1$ 和 $3$ 相对不那么“接近”，因此，$2 \times 2$ 大于 $1 \times 3$.

如图 01 所示，当 $a$ 和 $b$ 相差不多的时候是一个矩形，其面积 $S = ab = K$（其中，$K$ 是一个不为零的常数），但是，当 $a \rightarrow 0$ 时，$b \rightarrow + \infty$, 此时，原本的矩形其实就变成了一条“线段”，由于线段是没有面积的，因此，此时的面积 $S \rightarrow 0$:

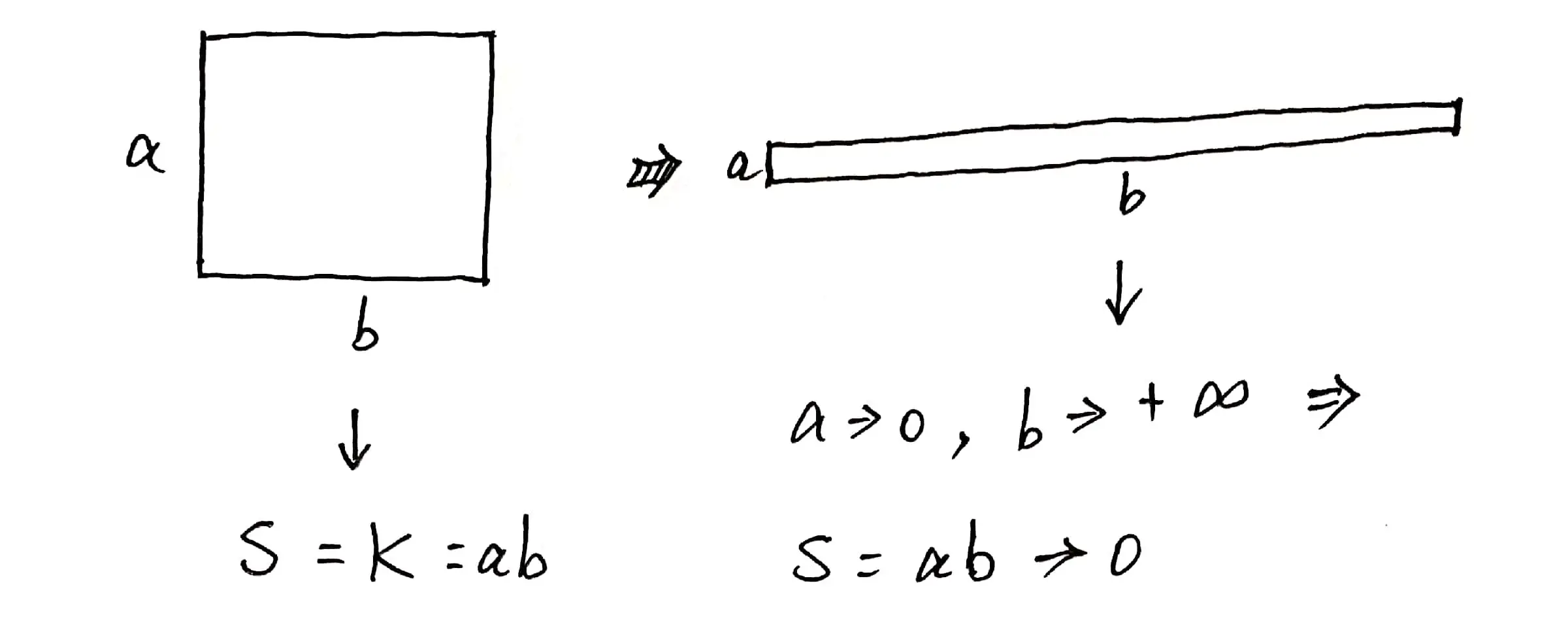
$a + b \geqslant 2 \sqrt{ab}$ $\Rightarrow$ $a + b \geqslant \sqrt{ab} + \sqrt{ab}$

该不等式表达的意思就是：

在【积】一定的情况下，两个数字越【接近】，相【加】所得的数就越【小】。

例如，$1 \times 4$ 和 $2 \times 2$ 都等于 $4$, 但是，由于 $1$ 与 $4$ 之间的距离相较于 $2$ 与 $2$ 之间的距离更大，因此，$1 + 4$ 大于 $2 + 2$.

由于 $\sqrt{ab}$ 相当于把 $a$ 与 $b$ 融合之后再通过开方的方式平分，因此，$\sqrt{ab}$ 加上 $\sqrt{ab}$ 就没有直接令 $a$ 与 $b$ 相加更大。

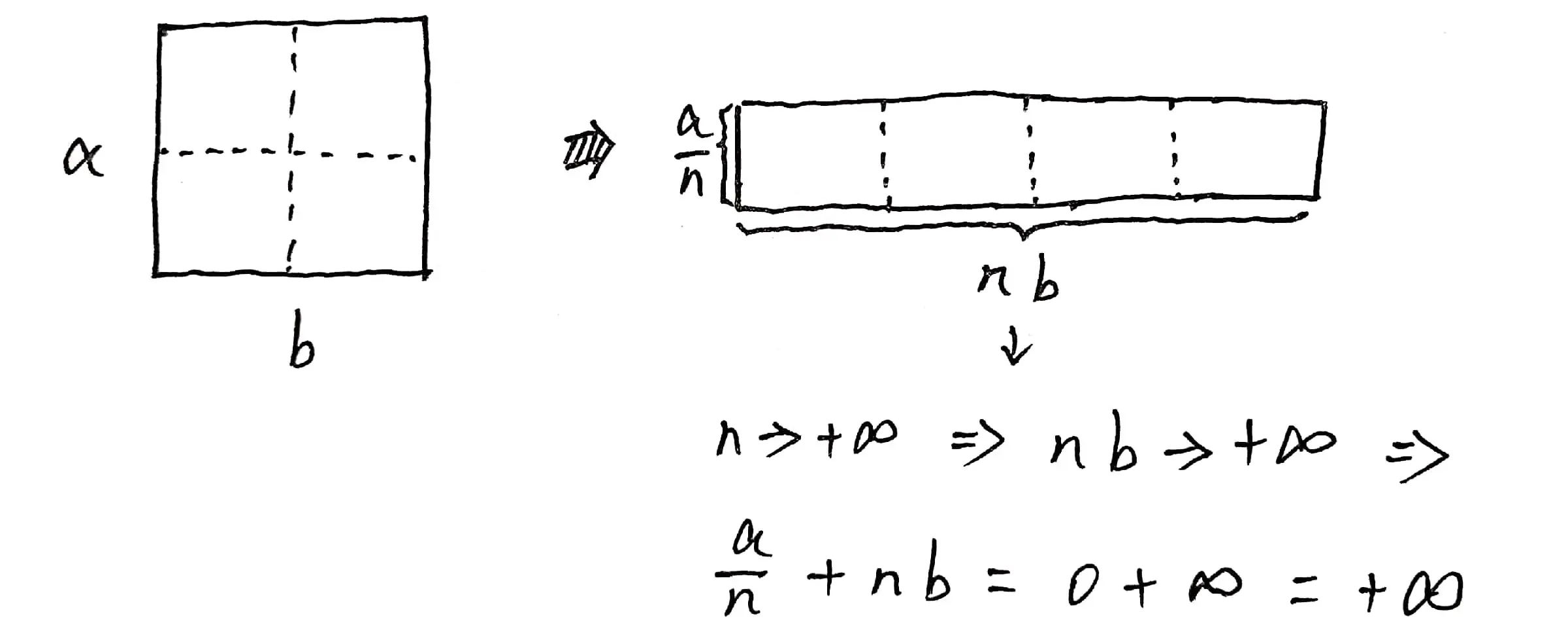
如图 02 所示，在保证面积不变的情况下，如果我们把左侧的矩形切成 $n \times n$ 份，之后再拼接成一排，就会发现，其“长”加“宽”的值由原来的 $a + b$ 变成了 $+ \infty$ 了：

---