与三次函数有三个交点？还是选择题？画图秒解！

一、题目

假设曲线 $y=x^{3}-3 x$ 与直线 $y=A$ 有 3 个不同的交点，则以下结论成立的是哪个？

(A) $A<3$.

(B) $A>-3$.

(C) $-2<A<2$.

(D) $A \neq 0$.

难度评级：

二、解析

满足题意得示意图如下：

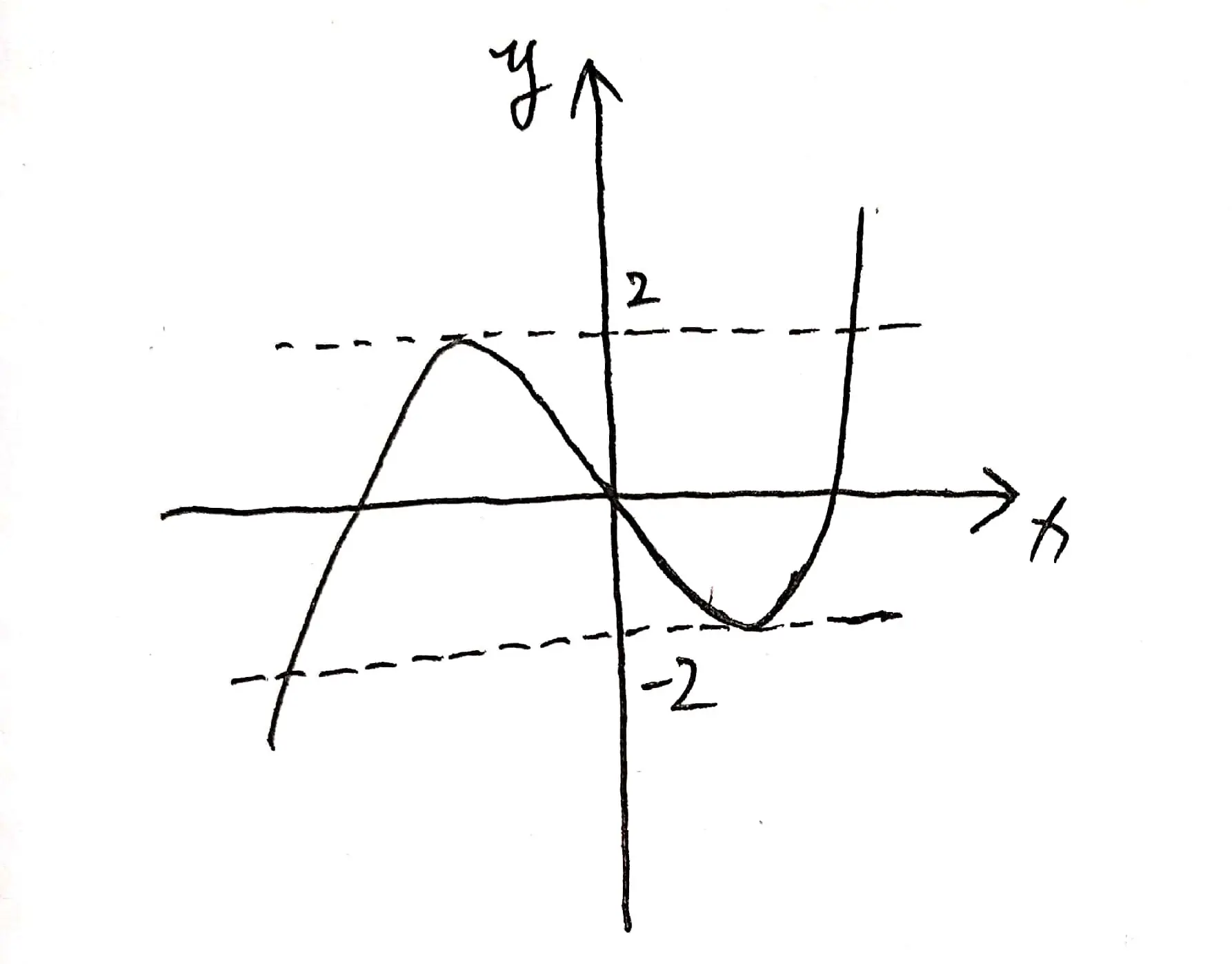
因此，只能选 C.

当然，如果这不是选择题，那么，我们就可以进行如下计算：

$$
y^{\prime}=3 x^{2}-3 \Rightarrow y^{\prime}=0 \Rightarrow x= \pm 1
$$

$$
x \in(-\infty,-1) \Rightarrow y^{\prime}>0 \Rightarrow y \text { 单调递增 }
$$

$$
x \in(-1,1) \Rightarrow y^{\prime}<0 \Rightarrow y \text { 单调递减 }
$$

$$
x \in(1,+\infty) \Rightarrow y^{\prime}>0 \Rightarrow y \text { 单调递增 }
$$

$$
x=-1 \Rightarrow y(-1)=-1+3=2
$$

$$
x=1 \Rightarrow y(1)=1-3=-2
$$

综上：

$$
-2<A<2
$$

---