单路径约束法：快速判断一个函数是否为周期函数

一、前言

通常，借助周期函数的性质可以帮助我们寻找解题思路，或者简化求解的难度——但这一切的前提是，我们必须知道一个函数是否是一个周期函数。

为此，荒原之梦网在一般的周期函数判断方法的基础上，提出了一种名为“单路径约束”的全新判断方式，帮助大家快速判断一个函数是否是周期函数。

本文用于判断函数的周期性，如果想判断函数的奇偶性可以参考《快速判断函数奇偶性的口诀》一文。

如果想了解周期函数的积分的有关性质，可以参考《周期函数的积分性质汇总》一文。

二、正文

一、常见的周期函数

为了快速判断一个函数是否是一个周期函数，我们首先需要掌握一些常见的周期函数——在考研数学中，我们可能遇到的周期函数一般都与三角函数有关：

$$y=\sin x$$

$$y=|\sin x|$$

$$y=\cos x$$

$$y=|\cos x|$$

$$y=\tan x$$

$$y=\cot x$$

二、四则运算对函数周期的影响

当两个周期函数的周期 $T_1$, $T_2$ 的比值 $\frac{T_1}{T_2}$ $=$ $\frac{p}{q}$ 是有理数的时候，则这两个周期函数进行加、减、乘、除的四则运算之后，得到的仍然是一个周期函数，且新函数的周期 $T$ $=$ $q{T}_1$ $=$ $p{T}_2$.

注意：

1. $T$ 不一定是新周期函数的最小正周期；
2. $p$ 和 $q$ 均为有理整数。

相反，如果两个周期函数的周期 $T_1$, $T_2$ 的比值 $\frac{T_1}{T_2}$ $=$ $\frac{p}{q}$ 不是有理数，则这两个周期函数进行加、减、乘、除的四则运算之后，得到的就一定不是一个周期函数。

三、复合运算对函数周期的影响

周期函数的本质，就是当自变量在 $X$ 轴上自由取值时，因变量的变化受到了“周期性的约束”，因此，判断一个函数是否是周期函数，最主要的着手点就是看这个函数是否受到了周期性的约束——

周期函数本身一定是受到周期性约束的，于是，在一个包含我们常见的周期性函数的式子中，看整个式子是否是周期性函数，就看这种周期性的约束是否能贯穿整个式子，此外，还要看这个式子中，是否还受到其他非周期性约束条件的影响——

如果来自一个周期函数的周期性约束能作用到整个式子，且这个式子不再受其他非周期函数的影响，那么这个式子整体也会表现出周期性约束，也就是周期函数“单路径约束”得到的仍是周期函数。例如，下面的 $(\sin x{)}^2$ 和 $e^{\cos x}$ 都是周期性函数，图中的红色箭头表示“单约束路径”：

注意：使用“单路径约束法”划线判断一个函数是否是周期函数时，一条约束路径只能以一个自变量为起点，同时在整个路径中不能再经过第二个单独的自变量——每一个单独的自变量都对应着一个约束路径。

$(\sin x{)}^2$ 的判断图示：

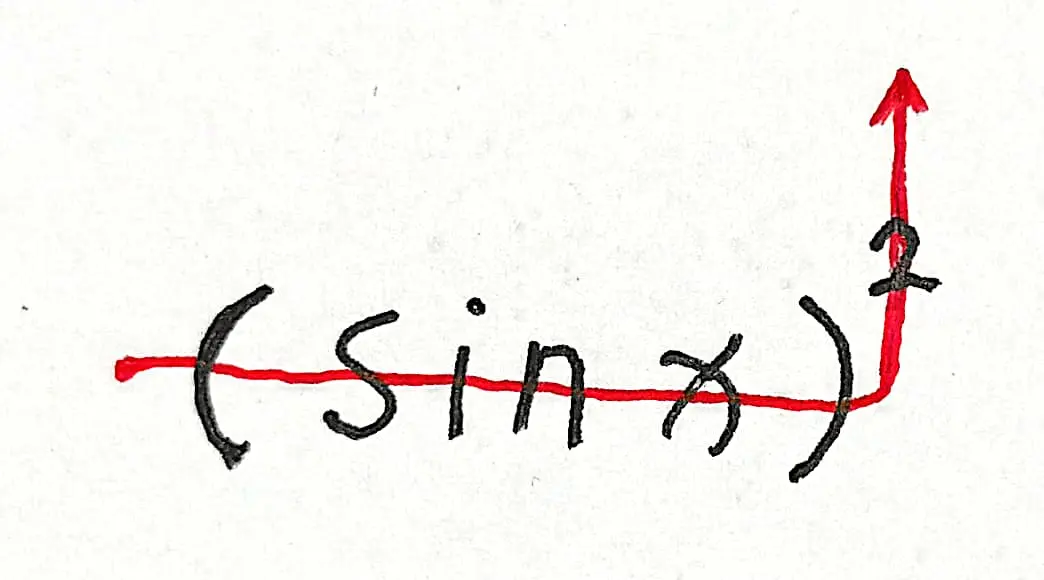
$(\sin x{)}^2$ 的函数图像：

$e^{\cos x}$ 的判断图示：

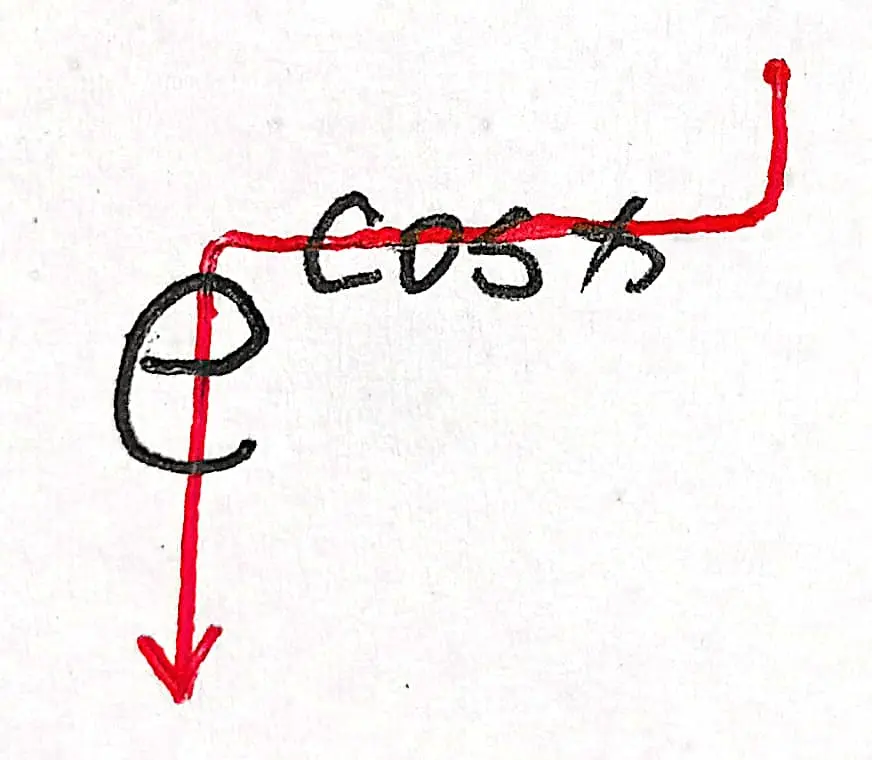
$e^{\cos x}$ 的函数图像：

此外，结合前面的“四则运算对函数周期的影响”可知，虽然 $e^{\cos x}$ $-$ $e^{-\sin x}$ 有两条“单约束路径”，但也是一个周期性函数：

$e^{\cos x}$ $-$ $e^{-\sin x}$ 的判断图示：

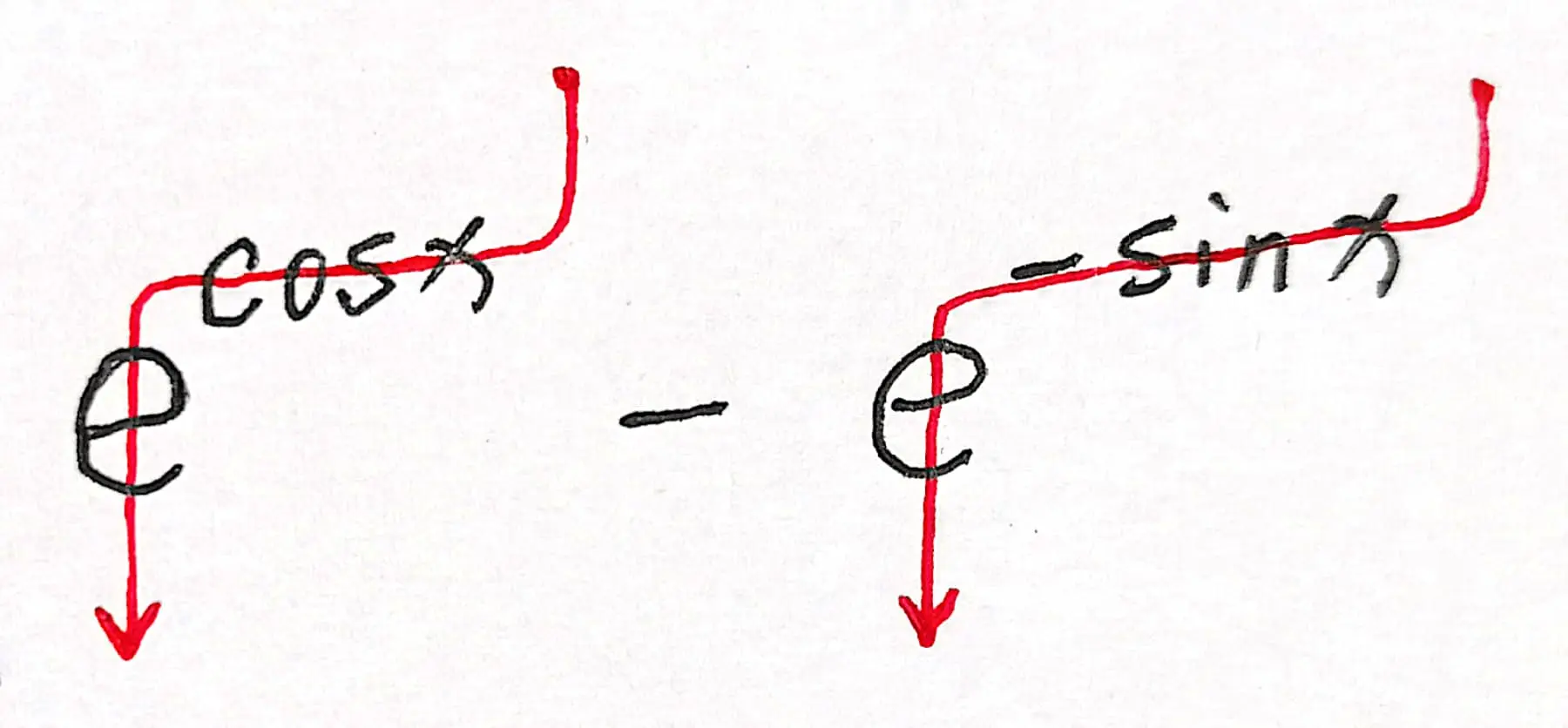
$e^{\cos x}$ $-$ $e^{-\sin x}$ 的函数图像：

但是，如果一个式子中出现了非周期函数的影响，那么，该式子就很可能不是一个周期函数了，例如，式子 $x\sin x$ 有一条单约束路径（红色），还有一条来自非周期函数 $x$ 的影响路径（蓝色），导致 $x\sin x$ 不是一个周期函数。

$x\sin x$ 的判断图示：

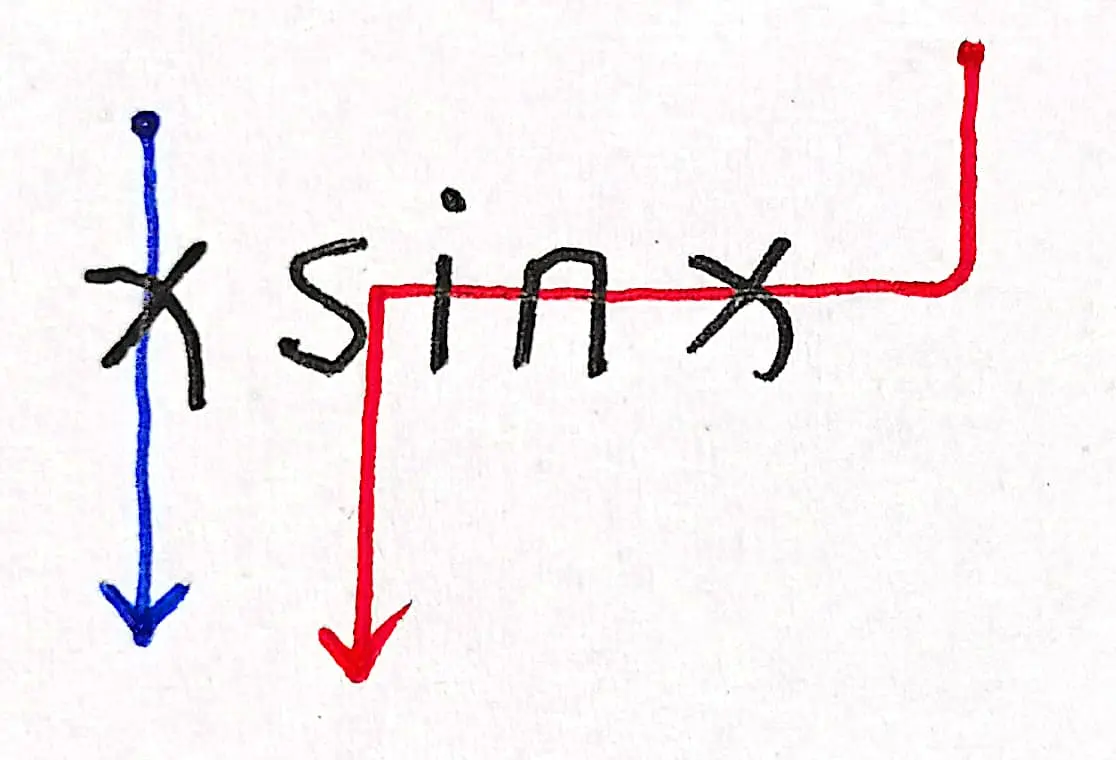
Tip

蓝色路径经过的 $x$ 虽然不是一个周期函数，但却是一个单调函数，所以，我们实际上可以用本文所提出的单路径约束法判断出 $x\sin x$ 是一个波纹函数。

zhaokaifeng.com

$x\sin x$ 的函数图像：

---