题目
设 $\left\{\begin{matrix}x = \arctan t,\\ y = 3t + t^{3},\end{matrix}\right.$ 则 $\frac{d^{2}y}{dx^{2}}|_{t=1} = ?$
继续阅读“2015年考研数二第09题解析”分类： 高等数学
2015年考研数二第06题解析
题目
设 $D$ 是第一象限中由曲线 $2xy=1$, $4xy=1$ 与直线 $y=x$, $y= \sqrt{3}x$ 围成的平面区域，函数 $f(x,y)$ 在 $D$ 上连续，则 $\iint_{D} f(x,y) \mathrm{~d} x \mathrm{d} y = ?$
$$
A. \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \mathrm{~d} \theta \int_{\frac{1}{2 \sin 2 \theta}}^{\frac{1}{\sin 2 \theta}} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r
$$
$$
B. \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \mathrm{~d} \theta \int_{\frac{1}{\sqrt{2 \sin 2 \theta}}}^{\frac{1}{\sqrt{\sin 2 \theta}}} f(r \cos \theta, r \sin \theta) r \mathrm{~d} r
$$
$$
C. \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \mathrm{~d} \theta \int_{\frac{1}{2 \sin 2 \theta}}^{\frac{1}{\sin 2 \theta}} f(r \cos \theta, r \sin \theta) \mathrm{~d} r
$$
$$
D. \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \mathrm{~d} \theta \int_{\frac{1}{\sqrt{2 \sin 2 \theta}}}^{\frac{1}{\sqrt{\sin 2 \theta}}} f(r \cos \theta, r \sin \theta) \mathrm{~d} r
$$
2015年考研数二第05题解析
题目
设函数 $f(u,v)$ 满足 $f(x + y, \frac{y}{x}) = x^{2} – y^{2}$, 则 $\frac{\partial f}{\partial u} |_{u=1,v=1}$ 和 $\frac{\partial f}{\partial v} |_{u=1,v=1}$ 依次是 $?$
$$
A. \frac{1}{2}, 0
$$
$$
B. 0, \frac{1}{2}
$$
$$
C. – \frac{1}{2}, 0
$$
$$
D. 0, – \frac{1}{2}
$$
2015年考研数二第04题解析
题目
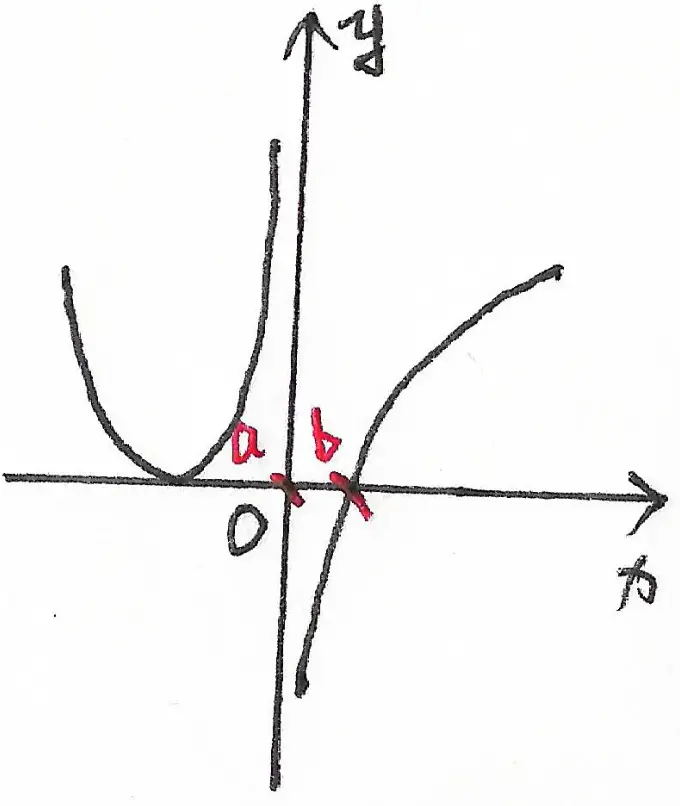
设函数 $f(x)$ 在 $(- \infty, +\infty)$ 内连续，其二阶导数 $f^{”}(x)$ 的图形如图 1 所示，则曲线 $y=f(x)$ 的拐点的个数为 $?$
$$
A. 0
$$
$$
B. 1
$$
$$
C. 2
$$
$$
D. 3
$$
2015年考研数二第03题解析
题目
设函数 $f(x) = \left\{\begin{matrix}
x^{\alpha} \cos \frac{1}{x^{\beta}}, x > 0\\
0, x \leqslant 0,
\end{matrix}\right.$ $(\alpha > 0, \beta > 0)$, 若 $f^{‘}(x)$ 在 $x=0$ 处连续，则 $?$
$$
A. \alpha – \beta > 1
$$
$$
B. 0 < \alpha – \beta \leqslant 1
$$
$$
C. \alpha – \beta > 2
$$
$$
D. 0 < \alpha – \beta \leqslant 2
$$
2015年考研数二第02题解析
题目
函数 $f(x) = \lim_{t \rightarrow 0}(1+\frac{\sin t}{x})^{\frac{x^{2}}{t}}$ 在 $(- \infty, + \infty)$ 内 $?$
$$
A. 连续
$$
$$
B. 有可去间断点
$$
$$
C. 有跳跃间断点
$$
$$
D. 有无穷间断点
$$
2015年考研数二第01题解析
题目
下列反常积分中收敛的是？
A. $\int_{2}^{+ \infty} \frac{1}{\sqrt{x}} dx$
B. $\int_{2}^{+ \infty} \frac{\ln x}{x} dx$
C. $\int_{2}^{+ \infty} \frac{1}{x \ln x} dx$
D. $\int_{2}^{+ \infty} \frac{x}{e^{x}} dx$
2016年考研数二真题解析汇总
2016年考研数二第13题解析
一、题目
编号：A2016213
已知动点 $P$ 在曲线 $y=x^{3}$ 上运动，记坐标原点与点 $P$ 间的距离为 $l$. 若点 $P$ 的横坐标对时间的变化率为常数 $v_{0}$, 则当点 $P$ 运动到点 $(1,1)$ 时，$l$ 对时间的变化率是 $?$
2016年考研数二第12题解析
题目
编号：A2016212
已知函数 $f(x)$ 在 $(- \infty, + \infty)$ 上连续，且 $f(x) = (x+1)^{2} + 2 \int_{0}^{x} f(t) \mathrm{~d} t$, 则当 $n \geqslant 2$ 时，$f^{(n)}(0) = ?$
2016年考研数二第11题解析
2016年考研数二第10题解析
题目
编号：A2016210
极限 $\lim_{n \rightarrow \infty}$ $\frac{1}{n^{2}}$ $($ $\sin \frac{1}{n}$ $+$ $2 \sin \frac{2}{n}$ $+…+$ $n \sin \frac{n}{n}$ $)$ $=?$
难度评级：
继续阅读“2016年考研数二第10题解析”2016年考研数二第09题解析
题目
编号：A2016209
曲线 $y$ $=$ $\frac{x^{3}}{1+x^{2}}$ $+$ $\arctan(1+x^{2})$ 的斜渐近线方程为 $?$
继续阅读“2016年考研数二第09题解析”2016年考研数二第06题解析
题目
编号：A2016206
已知函数 $f(x,y)=\frac{e^{x}}{x-y}$, 则 $?$
$$
A. f_{x}^{\prime} – f_{y}^{\prime} = 0
$$
$$
B. f_{x}^{\prime} + f_{y}^{\prime} = 0
$$
$$
C. f_{x}^{\prime} – f_{y}^{\prime} = f
$$
$$
D. f_{x}^{\prime} + f_{y}^{\prime} = f
$$
2016年考研数二第05题解析
题目
编号：A2016205
设函数 $f_{i}(x) (i=1,2)$ 具有二阶连续导数，且 $f_{i}^{”}(x_{0}) < 0 (i=1,2)$. 若两条曲线 $y=f_{i}(x) (i=1,2)$ 在点 $(x_{0}, y_{0})$ 处具有公切线 $y=g(x)$, 且在该点处曲线 $y=f_{1}(x)$ 的曲率大于 $y=f_{2}(x)$ 的曲率，则在 $x_{0}$ 的某个邻域内，有 $?$
$$
A. f_{1}(x) \leqslant f_{2}(x) \leqslant g(x)
$$
$$
B. f_{2}(x) \leqslant f_{1}(x) \leqslant g(x)
$$
$$
C. f_{1}(x) \leqslant g(x) \leqslant f_{2}(x)
$$
$$
D. f_{2}(x) \leqslant g(x) \leqslant f_{1}(x)
$$