GitHub CEO Nat Friedman 于当地时间 07 月 27 日发布数条推文回应了 GitHub 限制部分被美国制裁的国家的用户使用 GitHub 一事。
以下是 Nat Friedman 的原推及参考译文。
原推 1:
It is painful for me to hear how trade restrictions have hurt people. We have gone to great lengths to do no more than what is required by the law, but of course people are still affected. GitHub is subject to US trade law, just like any company that does business in the US.
翻译 1:
当我听到贸易制裁伤害到了人们的时候,我感到很痛苦。我们竭尽全力使我们的行为符合法律的要求,但是确实有人仍然受到了伤害。就像许多在美国开展业务的公司一样,GitHub 必须服从美国法律。
原推 2:
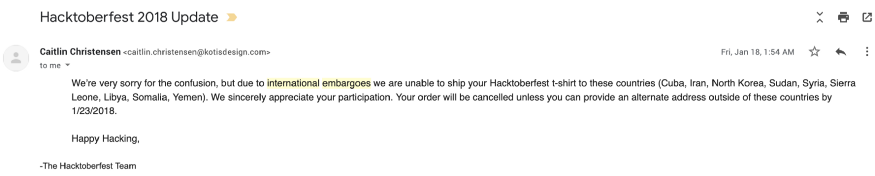
To comply with US sanctions, we unfortunately had to implement new restrictions on private repos and paid accounts in Iran, Syria, and Crimea.
Public repos remain available to developers everywhere – open source repos are NOT affected.
翻译 2:
为了遵守美国的制裁,非常不幸的是,我们必须对伊朗,叙利亚和克里米亚地区的私有仓库和付过费的账户施加限制。
公开的仓库仍然对所有地区的开发者开放,开源项目的仓库不受影响。
原推 3:
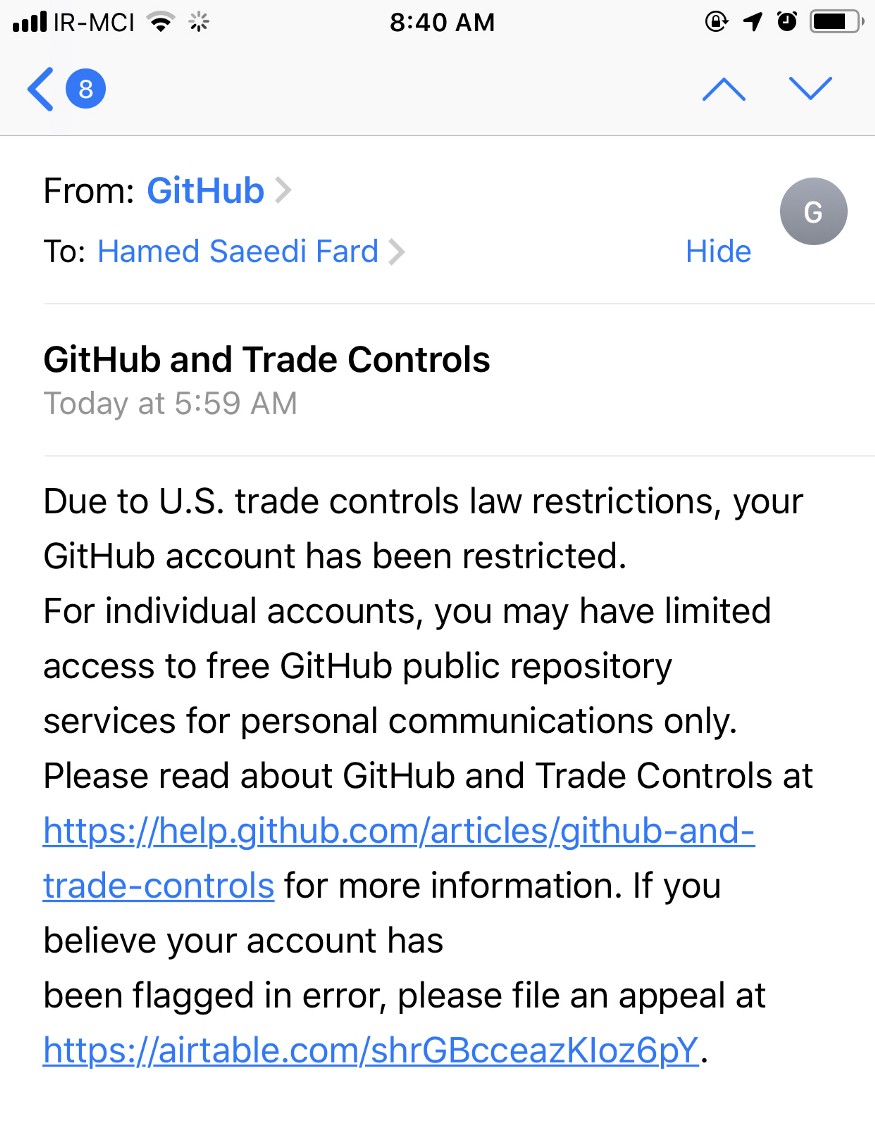
The restrictions are based on place of residence and location, not on nationality or heritage. If someone was flagged in error, they can fill out a form to get the restrictions lifted on their account within hours.
More info is on our policy page: https://help.github.com/en/articles/github-and-trade-controls
翻译 3:
这些限制是基于居住地点的,而不是国籍。如果有人被错误地标记了,他们可以填写一个表格来在数小时之内解除这些限制。
更多的信息在我们的政策页面:https://help.github.com/en/articles/github-and-trade-controls
原推 4:
Users with restricted private repos can also choose to make them public. Our understanding of the law does not give us the option to give anyone advance notice of restrictions.
翻译 4:
被限制的用户可以选择把私有仓库开源。根据我们对法律的理解,我们没有在账户被限制之前提前通知用户的选项。
原推 5:
We’re not doing this because we want to; we’re doing it because we have to. GitHub will continue to advocate vigorously with governments around the world for policies that protect software developers and the global open source community.
翻译 5:
我们这样做不是因为我们想这样做,我们这样做是因为我们不得不这么做。
GitHub 将继续向世界上各个国家大力倡导保护软件开发人员和开源社区的政策。
注:以上英文“原推”内容来自 Nat Friedman 的推特” @natfriedman”, 中文译文仅供参考,如果译文与原文存在冲突,请以原文为准。
EOF