By Emperorhoney – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=93020043
在数学中,“曲率”是用来描述几何体弯曲程度的一个量,例如曲线偏离其切直线的程度或者曲面偏离其切平面的程度都可以通过曲率来描述。
严格地说,曲率分为“外在曲率”和“内蕴曲率”两大类,在本文中,我们讨论的是嵌入到欧氏空间中的几何体所表现出来的“外在曲率”,这种曲率也是我们平时最常见到和使用到的一种曲率。
由于,当圆的半径趋于零时,该圆的弯曲程度几乎是 $- 180^{\circ}$, 而当圆的半径趋于无穷时,该圆几乎就是一条直线,弯曲程度也几乎是 $+ 180^{\circ}$, 因此,我们可以借助圆形来描述一条曲线上某点处的弯曲程度——在数学中,这个圆就是“曲率圆”。
如果说,一条曲线在某点处的曲率为 $k$, 那么该点所对应的曲率圆的半径,也就是曲率半径 $r$ $=$ $\frac{1}{k}$, 同时,该曲率圆的圆心与曲线上该点的连线必须垂直于过曲线上该点的切线(如图 01 所示)。
若曲线方程为直角坐标系下的 $y$ $=$ $f(x)$, 则其曲率 $k$ 的计算公式为:
$$
k = \frac{|y^{\prime \prime}|}{(1+y’^{2})^{\frac{3}{2}}}
$$
若曲线方程为极坐标系下的 $r$ $=$ $r(\theta)$, 则其曲率 $k(\theta)$ 为:
$$
k(\theta) = \frac{|r^{2} + 2r^{\prime 2}-r r^{\prime \prime}|}{(r^{2} + r^{\prime 2})^{\frac{3}{2}}}.
$$
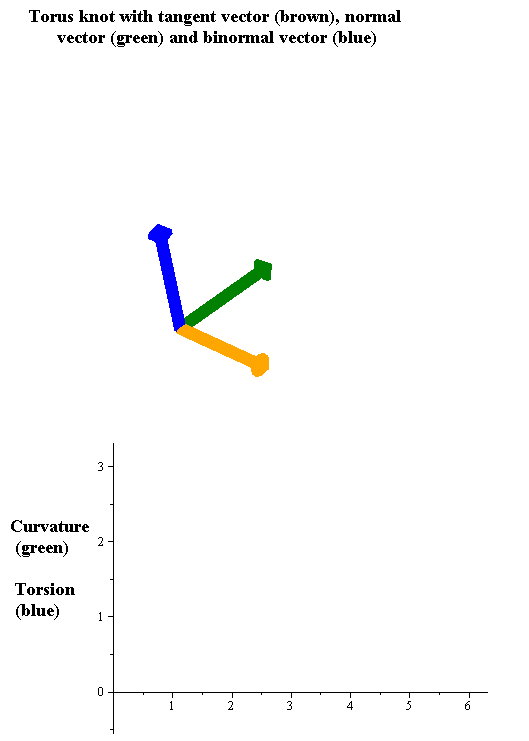
By Urs Hartl – Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18546393
参考资料:
[1]. https://en.wikipedia.org/wiki/Curvature
相关例题 
高等数学
涵盖高等数学基础概念、解题技巧等内容,图文并茂,计算过程清晰严谨。
线性代数
以独特的视角解析线性代数,让繁复的知识变得直观明了。
特别专题
通过专题的形式对数学知识结构做必要的补充,使所学知识更加连贯坚实。