题目
已知曲线 $L: y = \frac{4}{9} x^{2}$ $(x \geqslant 0)$, 点 $O(0, 0)$, 点 $A(0, 1)$. 设 $P$ 是 $L$ 上的动点, $S$ 是直线 $OA$ 与直线 $AP$ 及曲线 $L$ 所围图形的面积. 若 $P$ 运动到点 $(3, 4)$ 时沿 $x$ 轴正向的速度是 $4$, 求此时 $S$ 关于时间 $t$ 的变化率.
解析
根据题目描述,我们可以绘制出如图 01 所示的示意图,其中阴影部分就是直线 $OA$ 与直线 $AP$ 及曲线 $L$ 所围成的图形:
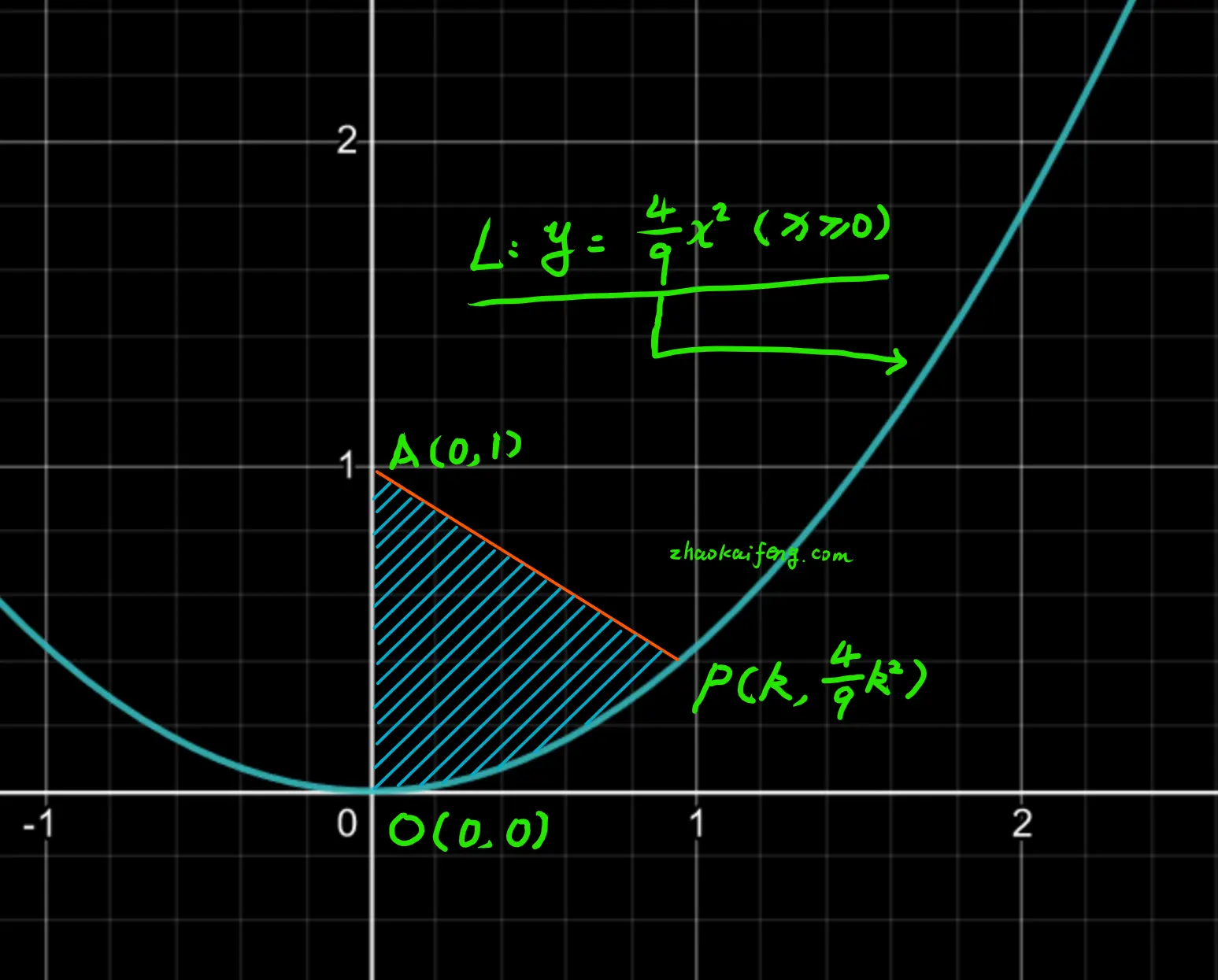
分析可知,要求解特定时间点时,面积 $S$ 关于时间 $t$ 的变化率,就是求在该时间点时,面积 $S$ 的微分 $\mathrm{d} S$ 与时间 $t$ 的微分 $\mathrm{d} t$ 之间的比值:$\frac{\mathrm{d} S}{\mathrm{d} t}$.
为此,我们首先要求出面积 $S$ 的表达式,过程如下:
设点 $P$ 的坐标为:$(k, \frac{4}{9} k^{2})$, 则:
由题可知,直线 $AP$ 的斜率为:
$$
\frac{\frac{4}{9} k^{2} – 1}{k – 0} = \frac{4}{9} k – \frac{1}{k}.
$$
于是,直线 $AP$ 的方程可表示为:
$$
y = (\frac{4}{9} k – \frac{1}{k}) x + 1.
$$
于是有:
$$
S = \int_{0}^{k} \Bigg[ (\frac{4}{9} k – \frac{1}{k}) x + 1 \Bigg] \mathrm{d} x – \int_{0}^{k} \frac{4}{9} x^{2} \mathrm{d} x \Rightarrow
$$
$$
S = (\frac{4}{9} k – \frac{1}{k}) \int_{0}^{k} x \mathrm{d} x + k – \frac{4}{9} \int_{0}^{k} x^{2} \mathrm{d} x \Rightarrow
$$
$$
S = (\frac{4}{9} k – \frac{1}{k}) \cdot \frac{1}{2} k^{2} + k – \frac{4}{9} \cdot \frac{1}{3} k^{3} \Rightarrow
$$
$$
S = \frac{2 k^{3}}{9} – \frac{k}{2} + k – \frac{4 k^{3}}{27} \Rightarrow
$$
$$
{\color{Red}
S = \frac{2 k^{3}}{27} + \frac{k}{2}} \Rightarrow
$$
$$
{\color{Red}
\frac{\mathrm{d} S}{\mathrm{d} k} = \frac{2 k^{2}}{9} + \frac{1}{2}}.
$$
于是:
$$
\frac{\mathrm{d} S}{\mathrm{d} t} \Rightarrow
$$
$$
\frac{\mathrm{d} S}{\mathrm{d} k} \cdot \frac{\mathrm{d} k}{\mathrm{d} t}.
$$
由于变量 $k$ 是点 $P$ 的横坐标,且由题可知,当点 $P$ 运动到点 $(3, 4)$ 时沿 $x$ 轴正向的速度是 $4$, 于是:
$$
{\color{Red}
\frac{\mathrm{d} k}{\mathrm{d} t} = 4}.
$$
进而:
$$
\frac{\mathrm{d} S}{\mathrm{d} k} \cdot \frac{\mathrm{d} k}{\mathrm{d} t} =
$$
$$
\frac{\mathrm{d} S}{\mathrm{d} k} \cdot 4 =
$$
$$
{\color{Red}
4(\frac{2 k^{2}}{9} + \frac{1}{2})}.
$$
将横坐标 $k = 3$ 代入上式,可知,当点 $P$ 运动到点 $(3, 4)$ 时,面积 $S$ 关于时间 $t$ 的变化率为:
$$
4(2 + \frac{1}{2}) = 8 + 2 = {\color{Red}10}.
$$