一、题目
设 $M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{(1+x)^{2}}{1+x^{2}}$ $dx$, $N$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{1+x}{e^{x}}$ $dx$, $K$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $(1+\sqrt{\cos x})$ $dx$, 则 ( )
( A ) $M$ $>$ $N$ $>$ $K$
( B ) $M$ $>$ $K$ $>$ $N$
( C ) $K$ $>$ $M$ $>$ $N$
( D ) $K$ $>$ $N$ $>$ $M$
二、解析
在解答题目时,能化简的要先化简,能计算出具体数值的要先计算出具体数值。
首先观察本题,发现 $M$ 对应的式子应该是可以化简或者通过积分计算出具体的数值。于是:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{(1+x)^{2}}{1+x^{2}}$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{1+x^{2}+2x}{1+x^{2}}$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $[\frac{1+x^{2}}{1+x^{2}}$ $+$ $\frac{2x}{1+x^{2}}]$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $[$ $1$ $+$ $\frac{2x}{1+x^{2}}]$ $dx$
计算到上面这一步之后,我们有两种方法可以继续上面的计算,一种方法是利用积分函数在对称区间上的性质,另一种是利用基本积分公式直接计算。
下面分别使用上述提到的两种方法展开计算。
方法一:利用积分函数在对称区间上的性质
这里说的“对称区间”指的是关于原点对称的区间,观察题目可知,题目中的积分函数的上限和下限组成的区间 $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$ 正好是关于原点对称的。
根据积分的几何意义,我们知道,奇函数在关于原点对称的对称区间上的积分是等于 $0$ 的。
$y$ $=$ $x$, $x$ $\in$ $(-\infty,$ $+\infty)$ 就是一个典型的奇函数,如图 1:
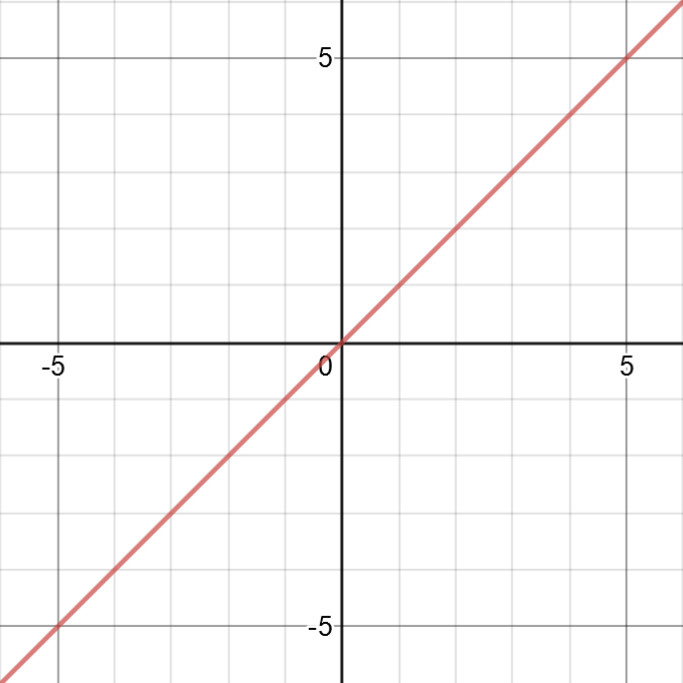
因此,接下来,我们如果能证明一个函数是奇函数,就可以证明这个函数在关于原点对称的区间上的积分是 $0$.
于是,令:
$f(x)$ $=$ $\frac{2x}{1+x^{2}}$
则:
$\frac{2(-x)}{1+(-x)^{2}}$ $=$ $-\frac{2x}{1+x^{2}}$ $\Rightarrow$ $f(-x)$ $=$ $-f(x)$.
因此 $f(x)$ $=$ $\frac{2x}{1+x^{2}}$ 是一个奇函数,于是:
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{2x}{1+x^{2}}$ $dx$ $=$ $0$.
即:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$.
方法二:利用基本积分公式直接计算
由前面的计算,我们已知,$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{2x}{1+x^{2}}$ $dx$, 于是,根据积分公式:
$d(x^{\mu})$ $=$ $\mu$ $x^{\mu-1}$ $dx$
我们可以令 $2x$ $dx$ $=$ $d(1+x^{2})$.
于是:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$ $+$ $\frac{d(1+x^{2})}{1+x^{2}}$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$ $+$ $\frac{1}{1+x^{2}}$ $d(1+x^{2})$.
接下来,根据基本积分公式:
$\int$ $\frac{1}{x}$ $dx$ $=$ $\ln |x|$ $+$ $c$.
我们有:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $+$ $\frac{1}{1+x^{2}}d(1+x^{2})$ $=$ $x$ $+$ $\ln |1+x^{2}|$ $+$ $c$ $|_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $=$ $\frac{\pi}{2}$ $+$ $|\ln[1+(\frac{\pi}{2})^{2}]|$ $+$ $c$ $-$ $(-\frac{\pi}{2})$ $-$ $|\ln[1+(-\frac{\pi}{2})^{2}]|$ $-$ $c$ $=$ $\frac{\pi}{2}+\frac{\pi}{2}$ $=$ $\pi$.
又因为,$M$ 的积分上限 $\frac{\pi}{2}$ 减去 $M$ 的积分下限 $-\frac{\pi}{2}$ 也等于 $\pi$.
根据定积分的基本性质:
$\int_{a}^{b}$ $1$ $dx$ $=$ $b$ $-$ $a$.
我们知道:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$.
补充:
如果是计算 $\int$ $\frac{2x}{1-x^{2}}$ $dx$, 则我们至少有以下两种计算方法:
$\int$ $\frac{2x}{1-x^{2}}$ $dx$ $=$ $-\int$ $\frac{1}{1-x^{2}}$ $=$ $-\ln |1-x^{2}|$ $+$ $c$;
或者:
$\int$ $\frac{2x}{1-x^{2}}$ $dx$ $=$ $\int$ $(\frac{1}{1-x}-\frac{1}{1+x})$ $dx$ $=$ $-\ln|x-1|$ $-$ $\ln|x+1|$ $+$ $c$ $=$ $-\ln|x^{2}-1|$ $+$ $c$.
至此,我们分别使用两种方法完成了对 $M$ 的化简计算。
根据定积分的比较定理:
设 $f(x)$ $\leqslant$ $g(x)$, $x$ $\in$ $[a,b]$, 则 $\int_{a}^{b}$ $f(x)$ $dx$ $\leqslant$ $\int_{a}^{b}$ $g(x)$ $dx$.
观察题目可知,题目中给出的三个定积分 $M$, $N$, $K$ 的上限和下限都是一样的,因此,我们可以使用上述比较定理比较他们的大小。
由于在 $M$, $N$, $K$ 中,我们目前已知的只有 $M$ 的数值,因此接下来我们先比较 $N$ 和 $K$ 中的积分函数与 $1$ 的大小关系。
首先来判断 $N$ 的积分函数和 $1$ 的大小关系。
当 $x$ $=$ $0$ 时,$1$ $+$ $x$ $=$ $e^{x}$ $=1$;
当 $x$ $<$ $0$ 时,$e^{x}$ 的减小速度小于 $1$ $+$ $x$ 的减小速度;
当 $x$ $>$ $0$ 时,$e^{x}$ 的增长速度大于 $1$ $+$ $x$ 的增长速度。
也就是说,在整个定义域内,$y$ $=$ $e^{x}$ 的函数图像始终在 $y$ $=$ $1$ $+$ $x$ 的上方或者和 $y$ $=$ $1$ $+$ $x$ 重合,他们二者的图像如图 2:
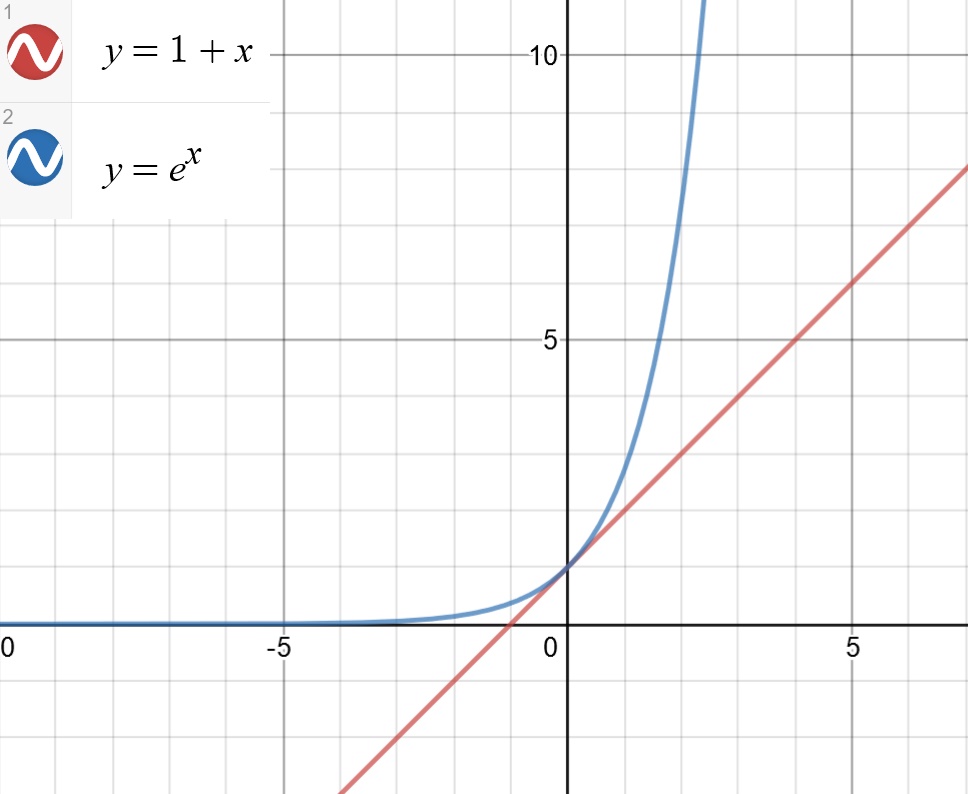
所以 $\frac{1+x}{e^{x}}$ $\leqslant$ $1$, $x$ $\in$ $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$. 再来判断 $K$ 的积分函数和 $1$ 的大小关系。
我们知道,当 $x$ $\in$ $[$ $-\frac{\pi}{2},$ $\frac{\pi}{2}$ $]$ 上时,$y$ $=$ $\cos x$ $\geqslant$ $0$ 的,如图 3:
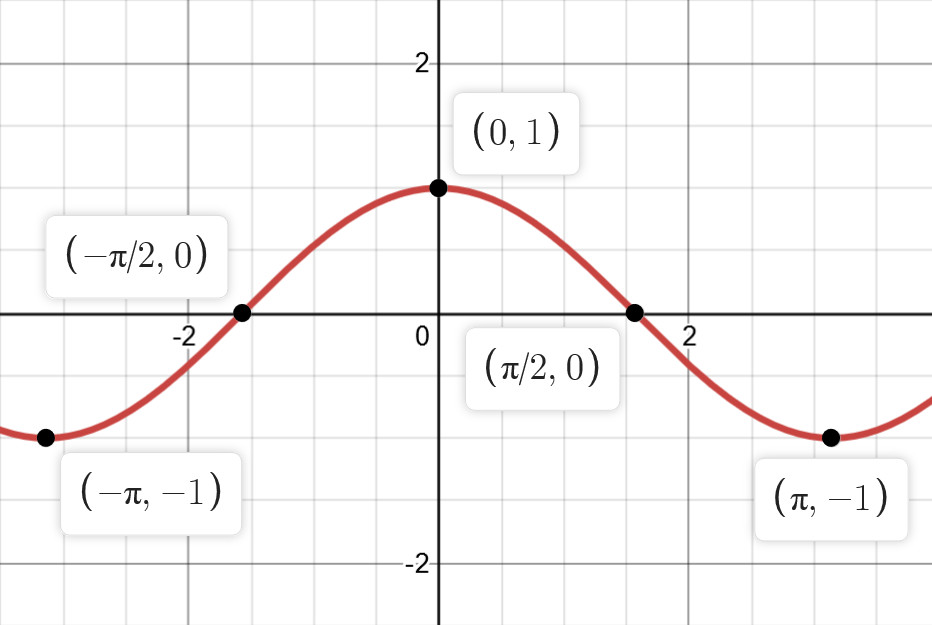
于是 $1$ $+$ $\sqrt{\cos x}$ $\geqslant$ $1$.
综上可知:
$K$ $\geqslant$ $M$ $\geqslant$ $N$, 正确选项是:C
EOF