一、前言 
本文侧重于从考试需要出发对摆线进行说明,摆线相关知识的说明详见:《摆线及其性质》
二、正文 
通常,摆线是通过参数方程表示出来的:
$$
\begin{cases}
& x = \textcolor{orangered}{ a } (t – \sin t) \\
& y = \textcolor{orangered}{ a } (1 – \cos t)
\end{cases}
$$
当然,有些题目也可能会把摆线的参数方程写成下面这种形式:
$$
x = a (t – \sin t), \ y = a (1 – \cos t)
$$
此外,摆线通常是由无数个“拱”组成的,但在考试中,我们一般只研究第一个“拱”,而要形成第一个拱,就需要上面参数方程中的参数 $t$ 的取值范围为:
$$
t \in (0, 2 \pi)
$$
这样的拱的长度是:
$$
2 \pi \textcolor{orangered}{ a }
$$
拱的高度是:
$$
2 \textcolor{orangered}{ a }
$$
当然,如果我们忘记了上面的规律,则只需要把 $\textcolor{springgreen}{ t = 0 }$ 和 $\textcolor{springgreen}{ t = 2 \pi }$ 分别代入到 $x = \textcolor{orangered}{ a } (t – \sin t)$ 中,就可以求解出摆线与 $X$ 轴的两个交点,同样的,把 $\textcolor{springgreen}{ t = \pi }$ 代入到 $y = \textcolor{orangered}{ a } (1 – \cos t)$ 就可以求解出摆线的最高点。
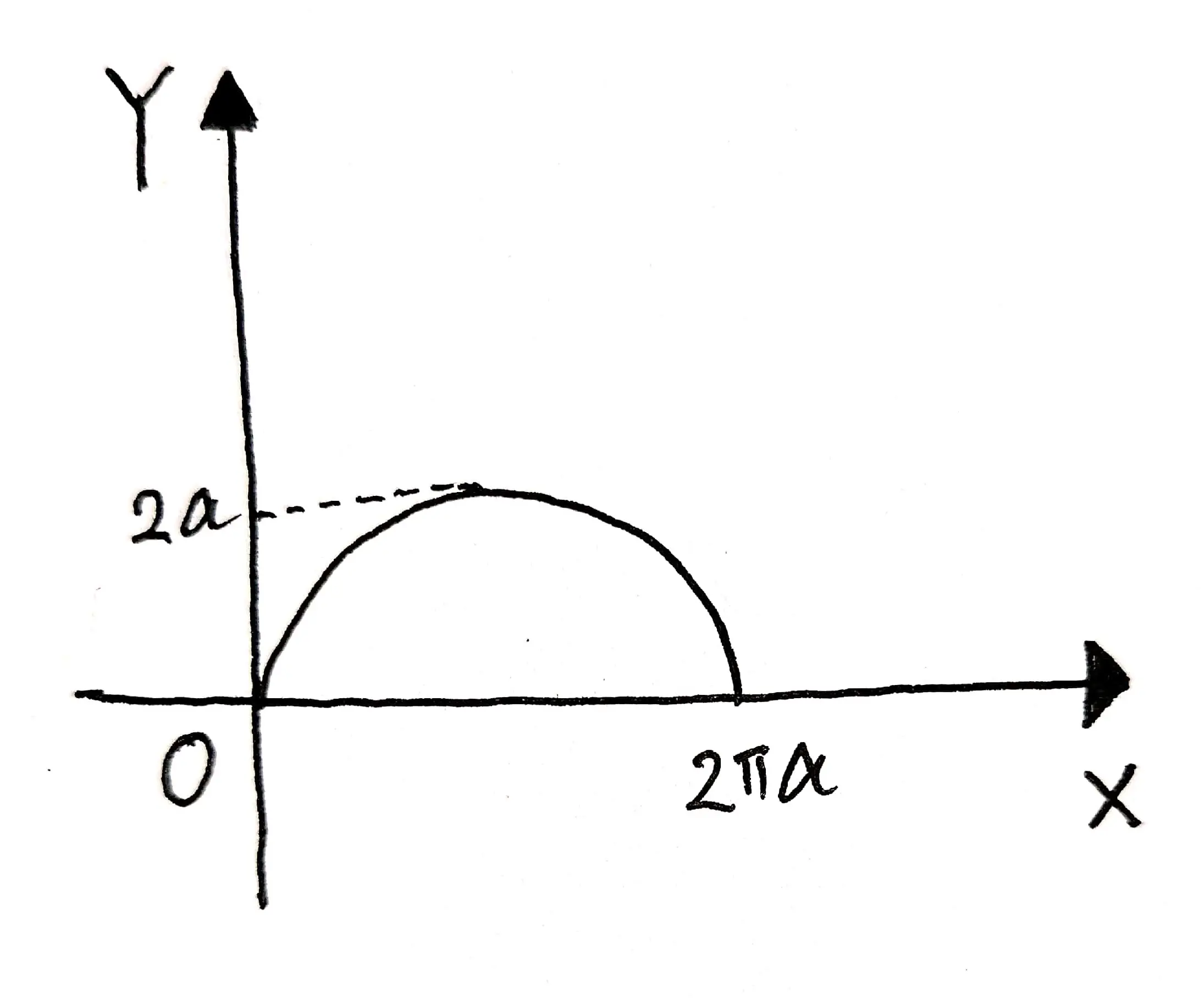
根据上面的分析,我们就可以手绘出摆线的大致示意图: