分类： 考研数学

一、题目

已知 $f(0)=0$, 则 $\lim \limits_{x \rightarrow 0} \frac{f\left(x^{2}\right)}{x^{2}}$ 存在是 $f(x)$ 在 $x=0$ 可导的充要条件吗？

难度评级：

一、题目

已知 $f(x)=\left\{\begin{array}{cc}\frac{g(x)-\mathrm{e}^{-x}}{x}, & x \neq 0 \\ 0, \quad x=0\end{array}\right.$, 其中 $g(x)$ 二阶连续可导, 且 $g(0)=1$, $g^{\prime}(0)=-1$, 则 $f^{\prime}(0)=?$ $f^{\prime}(x)$ 在 $(-\infty,+\infty)$ 上连续吗？

难度评级：

一、题目

已知 $f(x)=\left\{\begin{array}{cl}\mathrm{e}^{\frac{1}{x^{2}-1}}, & |x|<1 \\ x^{4}-b x^{2}+c, & |x| \geqslant 1\end{array}\right.$ 可导，则 $(b, c)=?$

难度评级：

一、前言

在本文中，我们将通过研究如下函数，来说明“间断点并不能决定一个函数是否是偶函数”这一结论。

$$
f(x) = e^{\frac{1}{x^{2} – 1}}
$$

难度评级：

一、题目

以下函数 $f[g(x)]$ 以 $x=0$ 为第二类间断点的是哪个？

(A) $f(u)=\ln \left(1+u^{2}\right), g(x)=\left\{\begin{array}{ll}\sin ^{2} x+(x+1)^{2}, & x \leqslant 0, \\ x^{2}+1, & x>0 .\end{array}\right.$

(B) $f(u)=\left\{\begin{array}{ll}1-u, & u \leqslant 0, \\ u^{2}+1, & u>0,\end{array}, g(x)=2 \cos x-1\right.$.

(C) $f(u)=\left\{\begin{array}{ll}\frac{\ln \left(1-u^{2}\right)}{u} \sin \frac{1}{u}, & u<0, \\ 1-\cos \sqrt{u}, & u \geqslant 0,\end{array}, g(x)=\left\{\begin{array}{ll}x, & x<0, \\ x+\frac{\pi^{2}}{4}, & x \geqslant 0 .\end{array}\right.\right.$.

(D) $f(u)=\mathrm{e}^{u^{2}}+1, g(x)=\left\{\begin{array}{ll}\frac{1}{x}, & x<0, \\ 0, & x=0, \\ \sin \frac{1}{x}, & x>0 .\end{array}\right.$

难度评级：

一、题目

已知 $f(x)$ 在 $[a,+\infty)$ 连续,则 “ $\exists x_{n} \in[a,+\infty)$ 有 $\lim \limits_{n \rightarrow \infty} x_{n}=+\infty$ 且 $\lim \limits_{n \rightarrow \infty} f\left(x_{n}\right)=\infty$ ”是 $f(x)$ 在 $[a,+\infty)$ 无界的

(A) 既非充分又非必要条件.
(B) 必要非充分条件.
(C) 充要条件.
(D) 充分非必要条件.

难度评级：

一、题目

请问，$f(x)$ 在 $x_{0}$ 点连续” 是 $|f(x)|$ 在 $x_{0}$ 点连续的

(A) 充分条件，但不是必要条件.
(B) 必要条件，但不是充分条件.
(C) 充分必要条件.
(D) 既不是充分，也不是必要条件.

难度评级：

一、题目

已知 $f(x)$ 在点 $x_{0}$ 的某邻域内有定义，且 $f(x)$ 在 $x_{0}$ 间断，则在点 $x_{0}$ 处必定间断的函数是哪个？

(A) $f(x) \sin x$.
(B) $f(x)+\sin x$.
(C) $f^{2}(x)$.
(D) $|f(x)|$.

难度评级：

一、题目

已知 $u_{n}$ $=$ $\left(1+\frac{1}{2}\right)\left(1+\frac{1}{2^{2}}\right) \cdots\left(1+\frac{1}{2^{n}}\right)$, 则下列命题正确的是哪个？

(A) $\lim \limits_{n \rightarrow \infty} u_{n}$ 不存在, 且 $\lim \limits_{n \rightarrow \infty} u_{n} \neq+\infty$.
(B) $\lim \limits_{n \rightarrow \infty} u_{n}=A>0$.
(C) $\lim \limits_{n \rightarrow \infty} u_{n}=+\infty$.
(D) $\lim \limits_{n \rightarrow \infty} u_{n}=0$.

难度评级：

一、题目

下列命题中正确的是哪个？

(A) 若 $\lim \limits_{x \rightarrow x_{0}} f(x) \geqslant \lim \limits_{x \rightarrow x_{0}} g(x) \Rightarrow$ 存在 $\delta>0$, 当 $0<\left|x-x_{0}\right|<\delta$ 时, $f(x) \geqslant g(x)$

(B) 若存在 $\delta>0$ 使得当 $0<\left|x-x_{0}\right|<\delta$ 时有 $f(x)>g(x)$ 且 $\lim \limits_{x \rightarrow x_{0}} f(x)=A_{0}$, $\lim \limits_{x \rightarrow x_{0}} g(x)=B_{0}$ 均存在, 则 $A_{0}>B_{0}$

(C) 若存在 $\delta>0$, 当 $0<\left|x-x_{0}\right|<\delta$ 时 $f(x)>g(x) \Rightarrow \lim \limits_{x \rightarrow x_{0}} f(x) \geqslant \lim \limits_{x \rightarrow x_{0}} g(x)$

(D) 若 $\lim \limits_{x \rightarrow x_{0}} f(x)>\lim \limits_{x \rightarrow x_{0}} g(x) \Rightarrow$ 存在 $\delta>0$, 当 $0<\left|x-x_{0}\right|<\delta$ 时有 $f(x)>g(x)$

难度评级：

一、题目

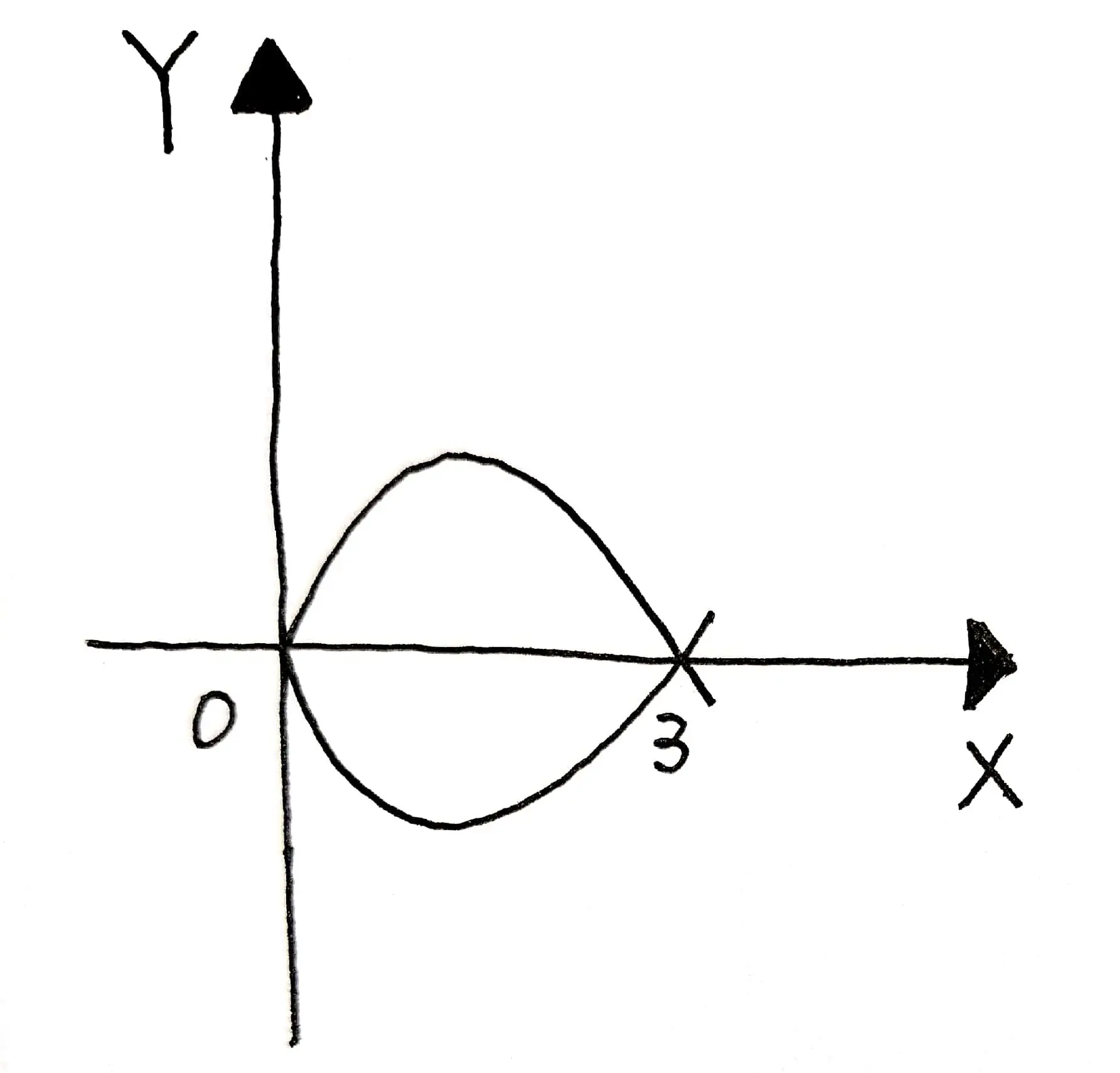
已知抛物叶形线的一部分公式为：

$$
y^{2}=\frac{x}{9}(3-x)^{2}(0 \leqslant x \leqslant 3)
$$

如图 01 所示，它围成的图形为 $M$, 则 $M$ 的面积 $A=?$, $M$ 的质心 (形心) $(\bar{x}, \bar{y})=?$

难度评级：

一、题目

由相交于三点 $\left(x_{1}, y_{1}\right)\left(x_{2}, y_{2}\right)\left(x_{3}, y_{3}\right)$ (其中 $\left.x_{1} < x_{2} < x_{3}\right)$ 的两曲线 $y=f(x) > $ $0, y=g(x) > 0$ 所围成的图形绕 $x$ 轴旋转一周所得旋转体体积为：

(A) $\int_{x_{1}}^{x_{3}} \pi[f(x)-g(x)]^{2} \mathrm{~d} x$
(B) $\int_{x_{1}}^{x_{3}} \pi\left[f^{2}(x)-g^{2}(x)\right] \mathrm{d} x$
(C) $\int_{x_{1}}^{x_{3}} \pi\left|f^{2}(x)-g^{2}(x)\right| \mathrm{d} x$
(D) $\left|\int_{x_{1}}^{x_{3}} \pi\left[f^{2}(x)-g^{2}(x)\right] \mathrm{d} x\right|$

难度评级：

一、题目

已知，无穷长直线 $L$ 的线密度为 $1$, 引力常数为 $k$, 则 $L$ 对距直线为 $a$ 的单位质点 $A$ 的引力是多少？

难度评级：

一、题目

已知，有曲线 $y=\sqrt{x-1}$, 过原点作其切线, 则以曲线、切线及 $x$ 轴所围成平面图形绕 $x$轴旋转一圈所得到的表面积是多少？

难度评级：