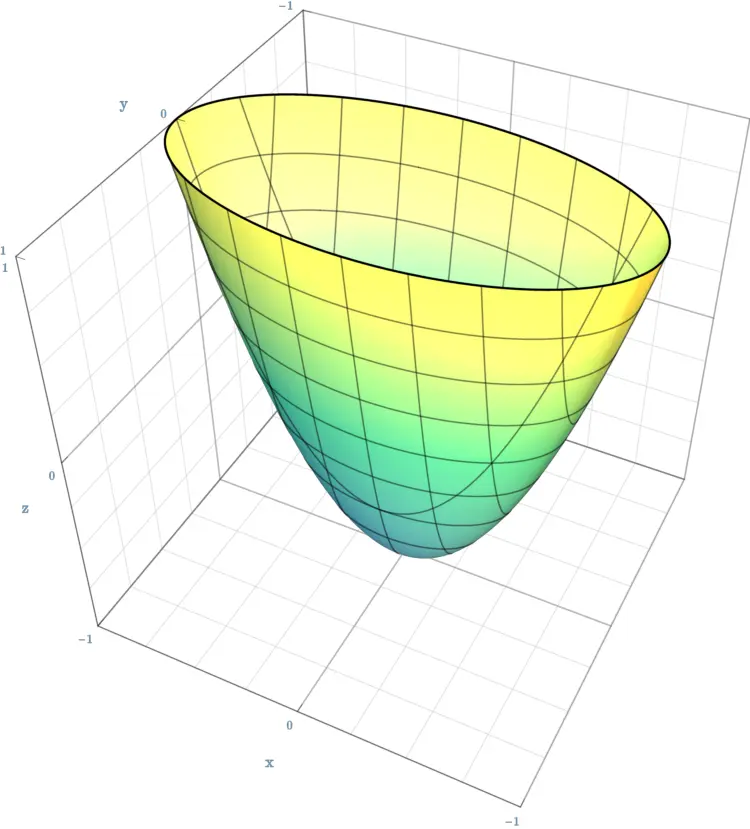
分类: 考研数学
偏导数 $\frac{\partial z}{\partial y}$(B012)
问题
已知函数 $z$ $=$ $f(x, y)$ 在 $(x, y)$ 的某邻域内有定义,且以下选项中的极限均存在,则 $\frac{\partial z}{\partial x}$ $=$ $?$选项
[A]. $\frac{\partial z}{\partial y}$ $=$ $\lim_{\Delta \rightarrow y}$ $\frac{f(x, y + \Delta y) – f(x, y)}{\Delta x}$[B]. $\frac{\partial z}{\partial y}$ $=$ $\lim_{\Delta \rightarrow y}$ $\frac{f(x, y + \Delta y) + f(x, y)}{\Delta y}$
[C]. $\frac{\partial z}{\partial y}$ $=$ $\lim_{\Delta \rightarrow y}$ $\frac{f(x, y + \Delta y) – f(x, y)}{\Delta y}$
[D]. $\frac{\partial z}{\partial y}$ $=$ $\lim_{\Delta \rightarrow y}$ $\frac{f(x + \Delta + x, y) – f(x, y)}{\Delta x}$
$\frac{\partial \textcolor{red}{z}}{\partial \textcolor{orange}{y}}$ $=$ $\lim_{\textcolor{yellow}{\Delta} \rightarrow \textcolor{orange}{y}}$ $\frac{f(\textcolor{cyan}{x}, \textcolor{orange}{y} + \textcolor{yellow}{\Delta} \textcolor{orange}{y}) – f(\textcolor{cyan}{x}, \textcolor{orange}{y})}{\textcolor{yellow}{\Delta} \textcolor{orange}{y}}$
偏导数 $\frac{\partial z}{\partial x}$(B012)
问题
已知函数 $z$ $=$ $f(x, y)$ 在 $(x, y)$ 的某邻域内有定义,且以下选项中的极限均存在,则 $\frac{\partial z}{\partial x}$ $=$ $?$选项
[A]. $\frac{\partial z}{\partial x}$ $=$ $\lim_{\Delta \rightarrow x}$ $\frac{f(x + \Delta x, y) – f(x, y)}{x}$[B]. $\frac{\partial z}{\partial x}$ $=$ $\lim_{\Delta \rightarrow x}$ $\frac{f(x, y + \Delta y) – f(x, y)}{\Delta x}$
[C]. $\frac{\partial z}{\partial x}$ $=$ $\lim_{\Delta \rightarrow x}$ $\frac{f(x + \Delta x, y) + f(x, y)}{\Delta x}$
[D]. $\frac{\partial z}{\partial x}$ $=$ $\lim_{\Delta \rightarrow x}$ $\frac{f(x + \Delta x, y) – f(x, y)}{f(x, y)}$
$\frac{\partial \textcolor{red}{z}}{\partial \textcolor{orange}{x}}$ $=$ $\lim_{\textcolor{yellow}{\Delta} \rightarrow \textcolor{orange}{x}}$ $\frac{f(\textcolor{orange}{x} + \textcolor{yellow}{\Delta} \textcolor{orange}{x}, \textcolor{cyan}{y}) \textcolor{yellow}{-} f(\textcolor{orange}{x}, \textcolor{cyan}{y})}{\textcolor{yellow}{\Delta} \textcolor{orange}{x}}$
空间曲线在 $zOx$ 平面上的投影曲线的方程(B011)
问题
已知空间曲线 $L$ 的一般方程为 $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$, 则该曲线在空间直角坐标系的 $zOx$ 平面上的投影曲线的方程该如何表示?选项
[A]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $y$ $\Rightarrow$ $\left\{\begin{array}{l} T(x, z)=y \\ y=0 \end{array}\right.$[B]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $z$ $\Rightarrow$ $\left\{\begin{array}{l} T(x, y)=0 \\ z=0 \end{array}\right.$
[C]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $y$ $\Rightarrow$ $\left\{\begin{array}{l} T(x, z)=0 \\ y=0 \end{array}\right.$
[D]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $x$ $\Rightarrow$ $\left\{\begin{array}{l} T(y, z)=0 \\ x=0 \end{array}\right.$
$\left\{\begin{array}{l} F(\textcolor{orange}{x}, \textcolor{orange}{y}, \textcolor{cyan}{z})=0 \\ G(\textcolor{orange}{x}, \textcolor{orange}{y}, \textcolor{cyan}{z})=0 \end{array}\right.$ $\Rightarrow$ 消去 $\textcolor{cyan}{y}$ $\Rightarrow$ $\left\{\begin{array}{l} T(\textcolor{orange}{x}, \textcolor{orange}{z})=0 \\ \textcolor{cyan}{y}=\textcolor{red}{0} \end{array}\right.$
空间曲线在 $yOz$ 平面上的投影曲线的方程(B011)
问题
已知空间曲线 $L$ 的一般方程为 $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$, 则该曲线在空间直角坐标系的 $yOz$ 平面上的投影曲线的方程该如何表示?选项
[A]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $x$ $\Rightarrow$ $\left\{\begin{array}{l} R(y, z)=x \\ x=0 \end{array}\right.$[B]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $y$ $\Rightarrow$ $\left\{\begin{array}{l} R(x, z)=0 \\ x=0 \end{array}\right.$
[C]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $x$ $\Rightarrow$ $\left\{\begin{array}{l} R(y, z)=0 \\ x=0 \end{array}\right.$
[D]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $x$ $\Rightarrow$ $\left\{\begin{array}{l} R(y, z)=0 \\ x=1 \end{array}\right.$
$\left\{\begin{array}{l} F(\textcolor{orange}{x}, \textcolor{orange}{y}, \textcolor{cyan}{z})=0 \\ G(\textcolor{orange}{x}, \textcolor{orange}{y}, \textcolor{cyan}{z})=0 \end{array}\right.$ $\Rightarrow$ 消去 $\textcolor{cyan}{x}$ $\Rightarrow$ $\left\{\begin{array}{l} R(\textcolor{orange}{y}, \textcolor{orange}{z})=0 \\ \textcolor{cyan}{x}=\textcolor{red}{0} \end{array}\right.$
空间曲线在 $xOy$ 平面上的投影曲线的方程(B011)
问题
已知空间曲线 $L$ 的一般方程为 $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$, 则该曲线在空间直角坐标系的 $xOy$ 平面上的投影曲线的方程该如何表示?选项
[A]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $y$ $\Rightarrow$ $\left\{\begin{array}{l} H(x, z)=0 \\ z=0 \end{array}\right.$[B]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $z$ $\Rightarrow$ $\left\{\begin{array}{l} H(x, y)=0 \\ z=0 \end{array}\right.$
[C]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $z$ $\Rightarrow$ $\left\{\begin{array}{l} H(x, y)=z \\ z=0 \end{array}\right.$
[D]. $\left\{\begin{array}{l} F(x, y, z)=0 \\ G(x, y, z)=0 \end{array}\right.$ $\Rightarrow$ 消去 $y$ $\Rightarrow$ $\left\{\begin{array}{l} H(x, y)=0 \\ z=0 \end{array}\right.$
$\left\{\begin{array}{l} F(\textcolor{orange}{x}, \textcolor{orange}{y}, \textcolor{cyan}{z})=0 \\ G(\textcolor{orange}{x}, \textcolor{orange}{y}, \textcolor{cyan}{z})=0 \end{array}\right.$ $\Rightarrow$ 消去 $\textcolor{cyan}{z}$ $\Rightarrow$ $\left\{\begin{array}{l} H(\textcolor{orange}{x}, \textcolor{orange}{y})=0 \\ \textcolor{cyan}{z}=\textcolor{red}{0} \end{array}\right.$
特殊的双叶双曲面的方程(B010)
问题
下列哪一项是 [特殊的双叶双曲面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{z^{2}}{b^{2}}$ $=$ $1$[B]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{z^{2}}{b^{2}}$ $=$ $-1$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{z^{2}}{a^{2}}$ $=$ $-1$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $\frac{z^{2}}{b^{2}}$ $=$ $-1$
$\frac{\textcolor{orange}{x}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{y}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{-}$ $\frac{\textcolor{orange}{z}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{b}^{\textcolor{yellow}{2}}}$ $=$ $\textcolor{red}{-1}$
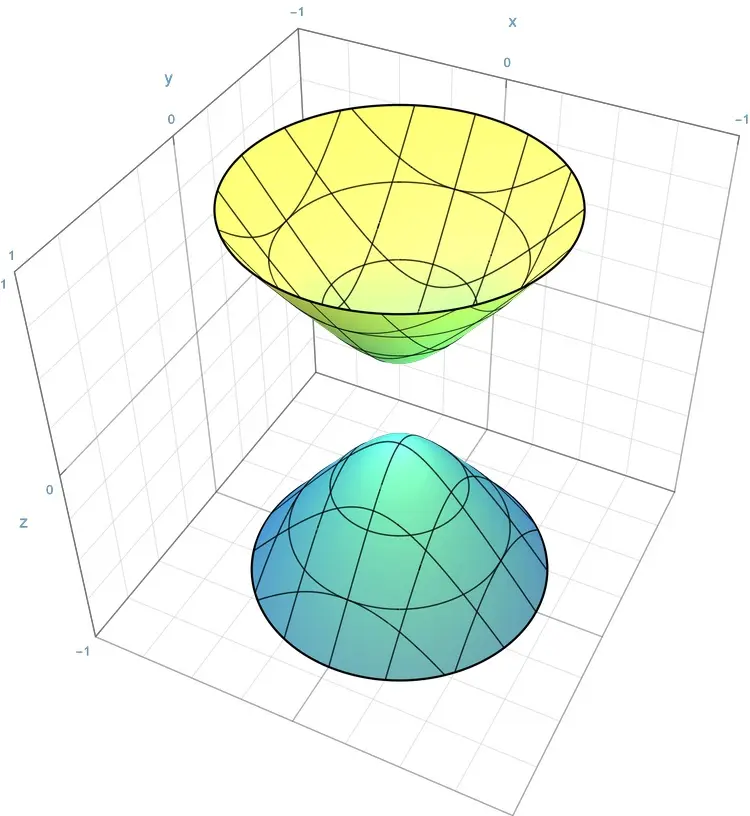
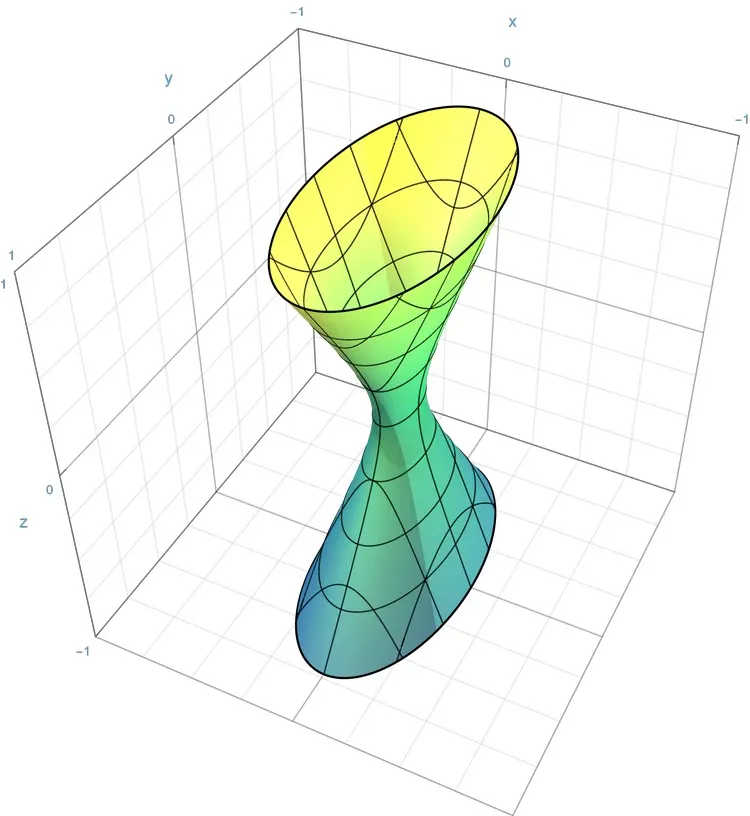
特殊的单叶双曲面的方程(B010)
问题
下列哪一项是 [特殊的单叶双曲面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $\frac{z^{2}}{b^{2}}$ $=$ $1$[B]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{z^{2}}{b^{2}}$ $=$ $0$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{z^{2}}{b^{2}}$ $=$ $1$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $1$
$\frac{\textcolor{orange}{x}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{y}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{-}$ $\frac{\textcolor{orange}{z}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{b}^{\textcolor{yellow}{2}}}$ $=$ $\textcolor{red}{1}$
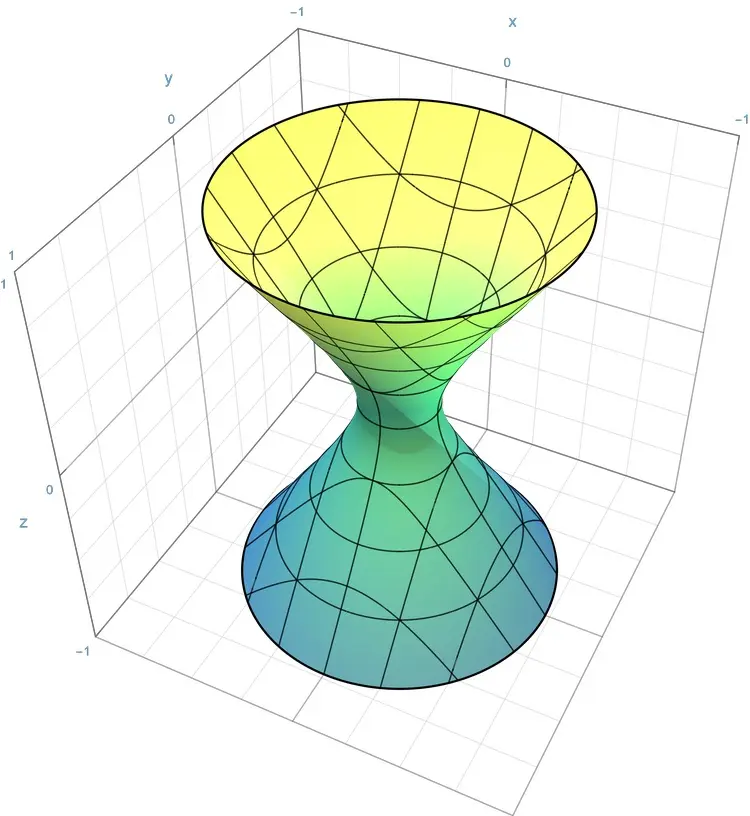
圆抛物面的方程(B010)
问题
下列哪一项是 [圆抛物面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $z$ $=$ $1$[B]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $z$ $=$ $0$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $0$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $z$ $=$ $0$
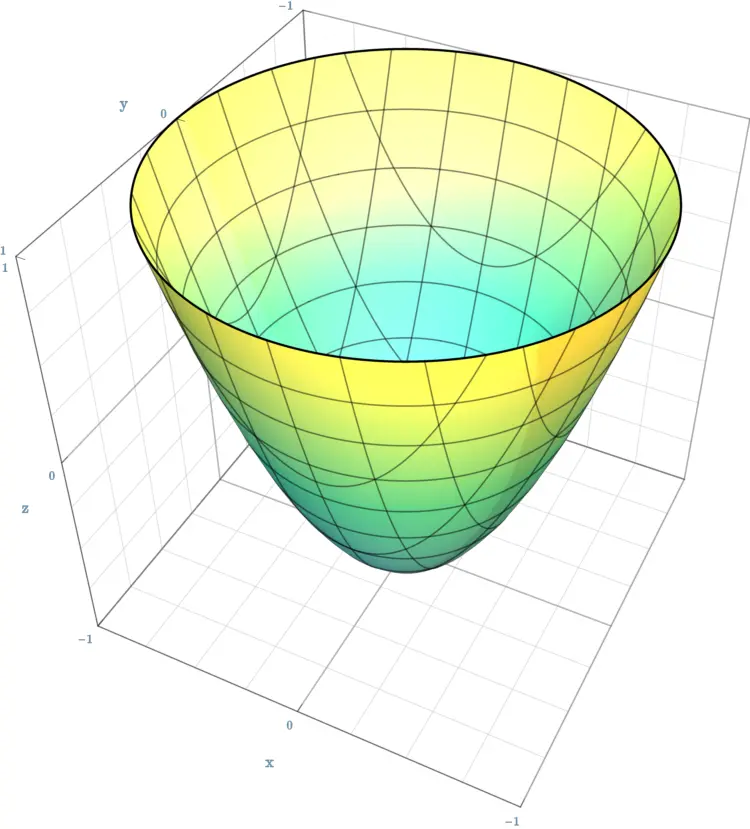
球面的方程(B010)
问题
下列哪一项是 [球面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $\frac{z^{2}}{a^{2}}$ $=$ $1$[B]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $+$ $\frac{z^{2}}{c^{2}}$ $=$ $1$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $\frac{z^{2}}{a^{2}}$ $=$ $-1$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $\frac{z^{2}}{a^{2}}$ $=$ $0$
$\frac{\textcolor{orange}{x}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{y}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{z}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $=$ $\textcolor{red}{1}$
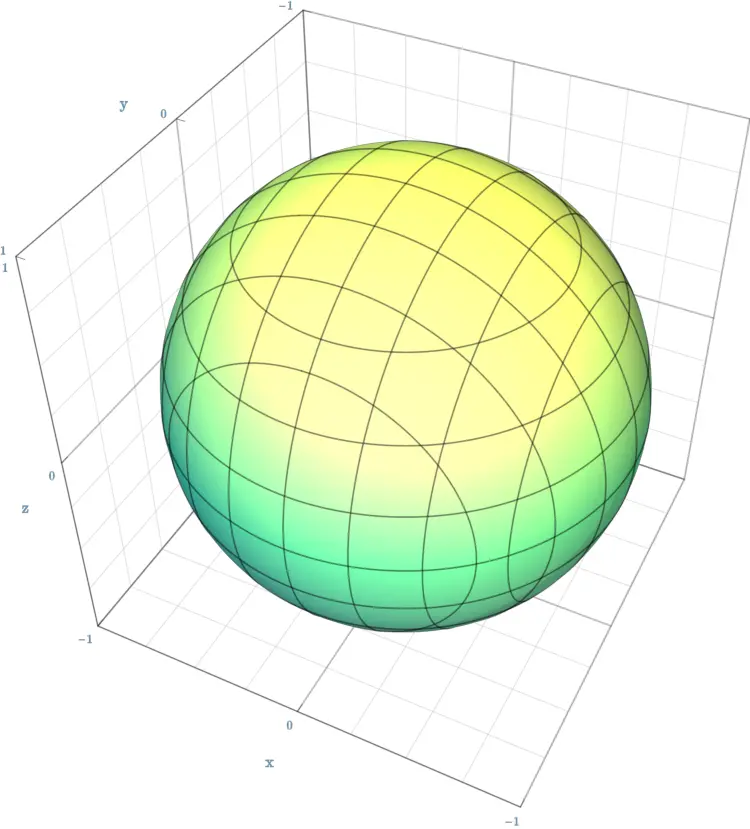
类球面的方程(B010)
问题
下列哪一项是 [类球面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $-$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{z^{2}}{b^{2}}$ $=$ $1$[B]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{z^{2}}{b^{2}}$ $=$ $0$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $\frac{z^{2}}{b^{2}}$ $=$ $1$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $+$ $\frac{z^{2}}{c^{2}}$ $=$ $1$
$\frac{\textcolor{orange}{x}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{y}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{z}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{b}^{\textcolor{yellow}{2}}}$ $=$ $\textcolor{red}{1}$
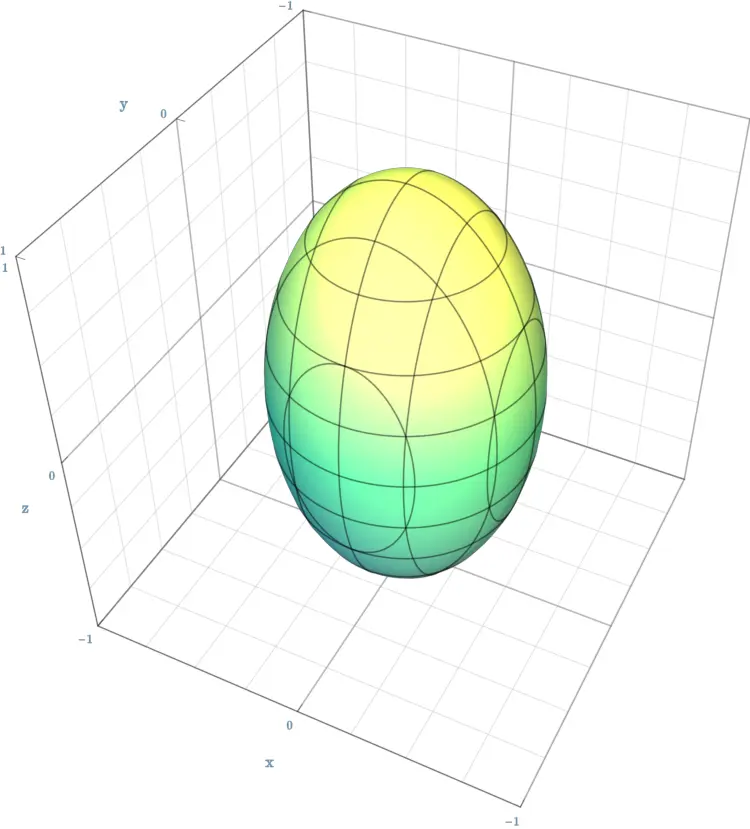

双叶双曲面的方程(B010)
问题
下列哪一项是 [双叶双曲面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $1$[B]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $\frac{z^{2}}{c^{2}}$ $=$ $-1$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $0$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{a^{2}}{c^{2}}$ $=$ $-1$
$\frac{\textcolor{orange}{x}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{y}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{b}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{-}$ $\frac{\textcolor{orange}{z}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{c}^{\textcolor{yellow}{2}}}$ $=$ $\textcolor{red}{-1}$
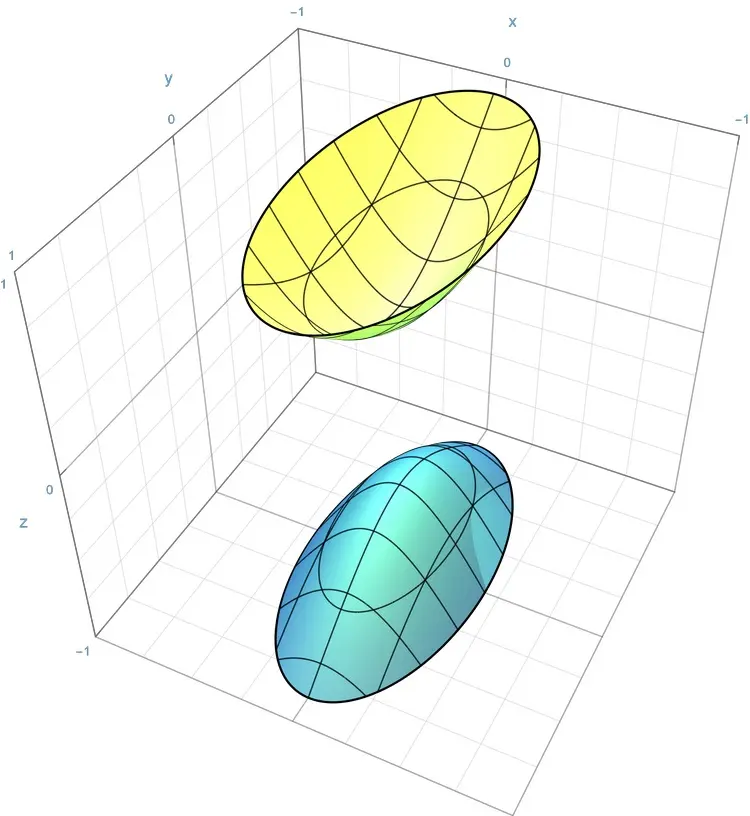
单叶双曲面的方程(B010)
问题
下列哪一项是 [单叶双曲面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $1$[B]. $\frac{x^{2}}{a^{2}}$ $-$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $1$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $+$ $\frac{z^{2}}{c^{2}}$ $=$ $1$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $0$
$\frac{\textcolor{orange}{x}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{y}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{b}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{-}$ $\frac{\textcolor{orange}{z}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{c}^{\textcolor{yellow}{2}}}$ $=$ $\textcolor{red}{1}$
双曲抛物面的方程(B010)
问题
下列哪一项是 [双曲抛物面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $+$ $z$ $=$ $0$[B]. $\frac{x^{2}}{a^{2}}$ $-$ $\frac{y^{2}}{b^{2}}$ $-$ $z$ $=$ $1$
[C]. $\frac{x^{2}}{a^{2}}$ $-$ $\frac{y^{2}}{b^{2}}$ $-$ $z$ $=$ $0$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $z$ $=$ $0$
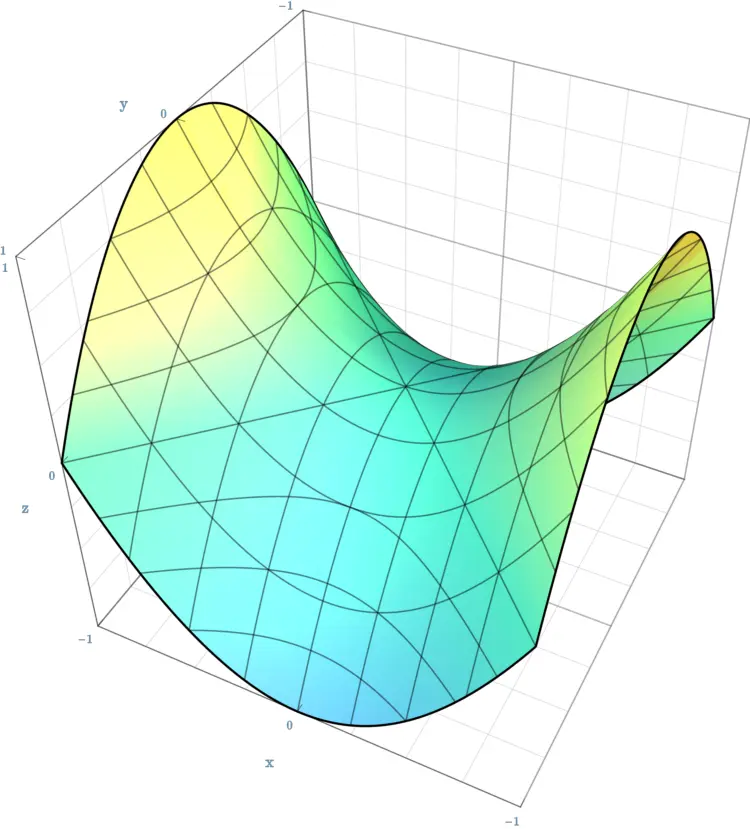
椭圆抛物面的方程(B010)
问题
下列哪一项是 [椭圆抛物面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $z$ $=$ $0$[B]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $z$ $=$ $0$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $+$ $z$ $=$ $0$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $z$ $=$ $1$