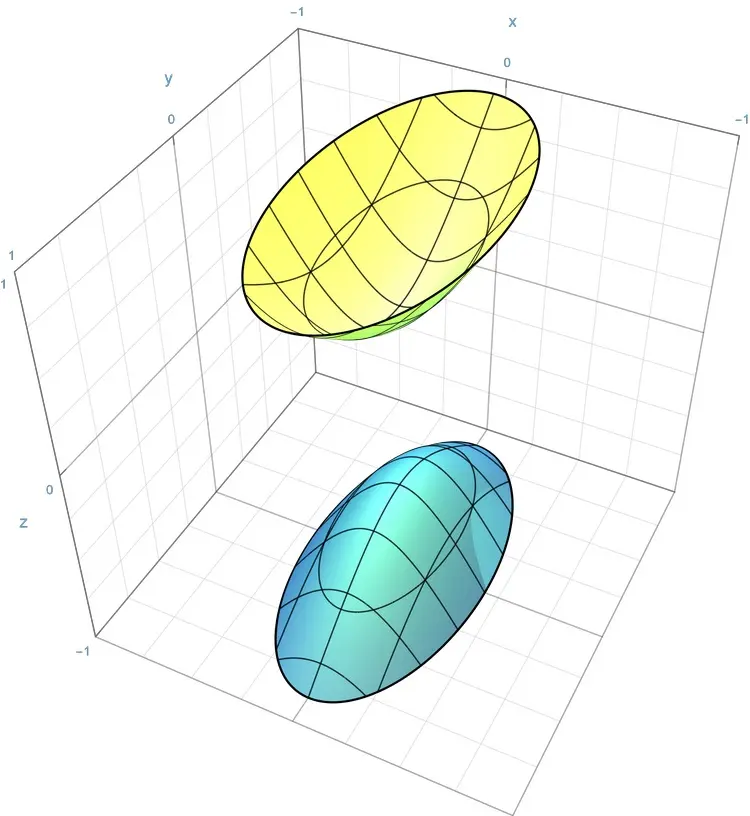
问题
下列哪一项是 [双叶双曲面] 的方程?其中,$a$, $b$, $c$ 分别表示位于 $x$ 轴、$y$ 轴和 $z$ 轴上的半轴.
选项
[A]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $-$ $\frac{a^{2}}{c^{2}}$ $=$ $-1$[B]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $1$
[C]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{a^{2}}$ $+$ $\frac{z^{2}}{c^{2}}$ $=$ $-1$
[D]. $\frac{x^{2}}{a^{2}}$ $+$ $\frac{y^{2}}{b^{2}}$ $-$ $\frac{z^{2}}{c^{2}}$ $=$ $0$
$\frac{\textcolor{orange}{x}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{a}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{+}$ $\frac{\textcolor{orange}{y}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{b}^{\textcolor{yellow}{2}}}$ $\textcolor{yellow}{-}$ $\frac{\textcolor{orange}{z}^{\textcolor{yellow}{2}}}{\textcolor{cyan}{c}^{\textcolor{yellow}{2}}}$ $=$ $\textcolor{red}{-1}$