一、题目
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $(\frac{\sin x}{1+\cos x}$ $+$ $|x|)$ $dx$ $=$__.
二、解析
本题存在(关于原点对称的)对称区间 “$[-\frac{\pi}{2}$, $\frac{\pi}{2}]$”, 在求积分的时候,如果看到这样的对称区间,则要考虑被积函数是不是奇函数或者偶函数。如果是奇函数,则其在对称区间上的积分为 $0$, 如果是偶函数,则我们可以只计算其大于 $0$ 或者小于 $0$ 方向上的积分,之后再乘以 $2$ 即可获得整个积分区间上的积分数值。
由于:
$\frac{\sin (-x)}{1+\cos(-x)}$ $=$ $\frac{-\sin x}{1+\cos x}$ $\Rightarrow$ $f(-x)$ $=$ $-f(x)$.
因此,$f(x)$ $=$ $\frac{\sin x}{1+\cos x}$ 是一个奇函数,因此,其在对称区间 $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$ 上的积分为 $0$.
又由于:
$|-x|$ $=$ $|x|$ $\Rightarrow$ $g(-x)$ $=$ $g(x)$.
因此,$g(x)$ $=$ $|x|$ 是一个偶函数。
于是:
原式 $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $|x|$ $dx$ $=$ $2$ $\int_{0}^{\frac{\pi}{2}}$ $x$ $dx$ $=$ $2$ $\cdot$ $\frac{1}{2}x^{2}|_{0}^{\frac{\pi}{2}}$ $=$ $\frac{\pi^{2}}{4}$.
当然,本题除了可以使用积分的原理计算之外,还可以画图计算面积,如图 1:
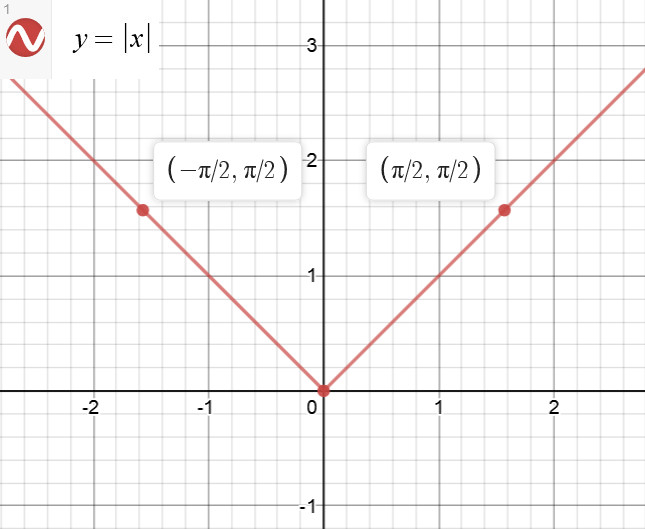
根据上图,我们有:
$\frac{\pi}{2}$ $\cdot$ $\frac{\pi}{2}$ $\cdot$ $\frac{1}{2}$ $\cdot$ $2$ $=$ $\frac{\pi^{2}}{4}$.
综上可知,本题的正确答案是:$\frac{\pi^{2}}{4}$.
EOF