一、前言 
在本文中,荒原之梦考研数学将通过图示的方式,给大家阐述清楚数列的有界、发散、收敛这三个概念之间的异同点,方便大家在其他辅导资料中常见的定义和举特例的方式之外,用更加形象的方式理解这三者之间的区别。
Tip
在本的示意图中:
zhaokaifeng.com
[1]. 横坐标表示数列的项数 $n$, 从左向右依次增大;
[2]. 纵坐标表示数列的值 $\left\{ x_{n} \right\}$, 从下到上依次增大;
[3]. 同一个坐标系中不同颜色的点对应的项数 $n$ 不相等,但都属于同一个数列 $\left\{ x_{n} \right\}$
二、正文 
§1. 数列有界不一定收敛
下面这个图中的数列就是一个有界数列(上下两条白色虚线就是界限,下同),但由于其在 $n \rightarrow \infty$ 的时候,$\left\{ x_{n} \right\}$ 的值是不断变化的,所以就没有“收敛”:
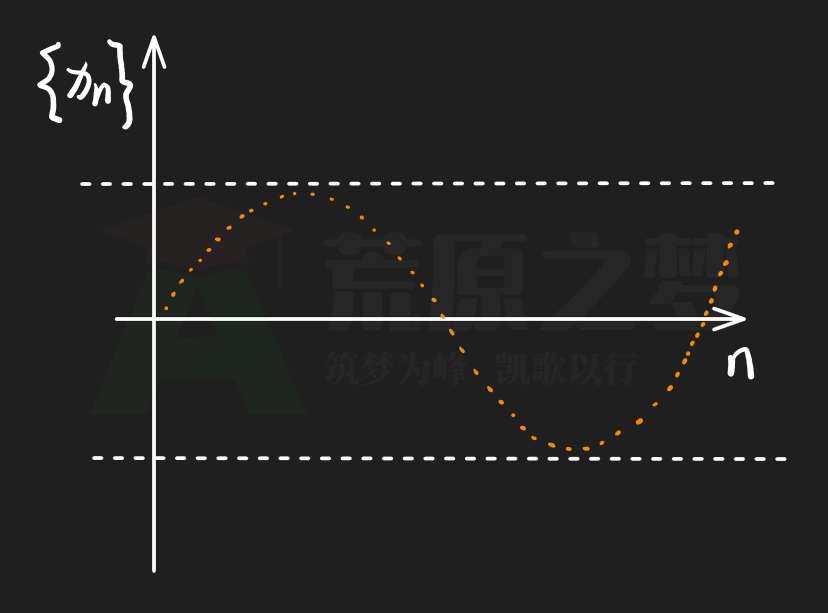
当然,下面这个数列同时存在两条不断变化的取值,也是一个有界但不收敛的数列:
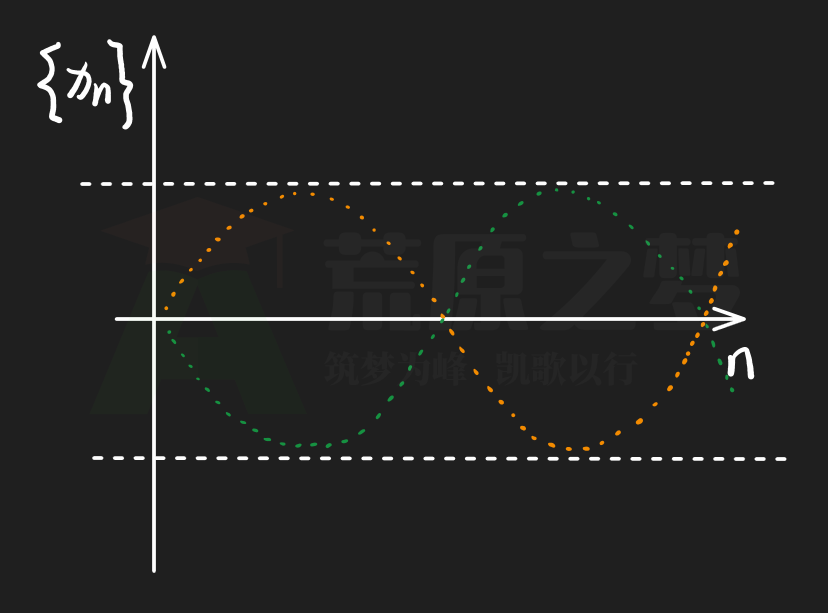
§2. 数列有界可能发散,数列发散也可能有界
下面这个数列很明显是一个发散数列:
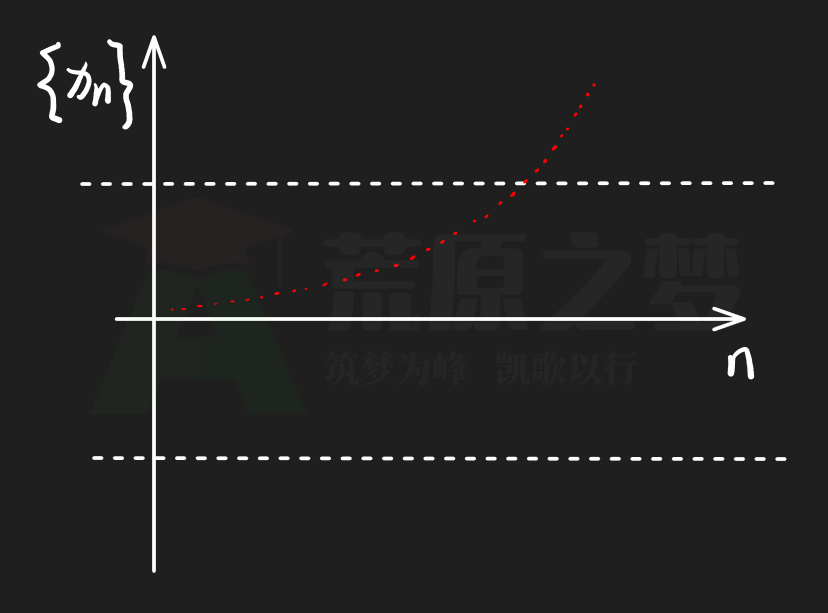
下面这个同时有两条发散方向的数列,更是一个发散数列:
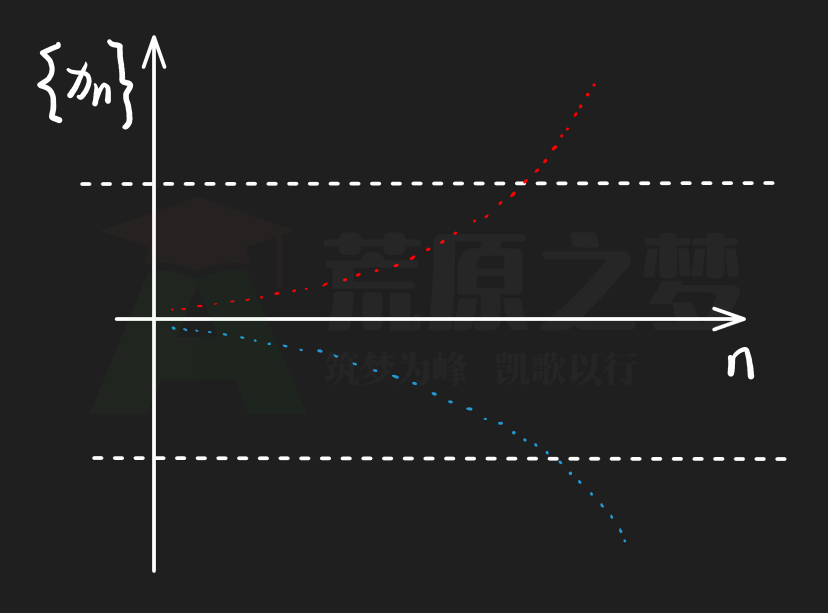
但是,前面的图 02 也是一个发散数列,同时也是一个有界数列:

§3. 数列有界且不发散且一定收敛
收敛数列一定有界,收敛数列也一定不发散,下面就是一个典型的收敛数列:
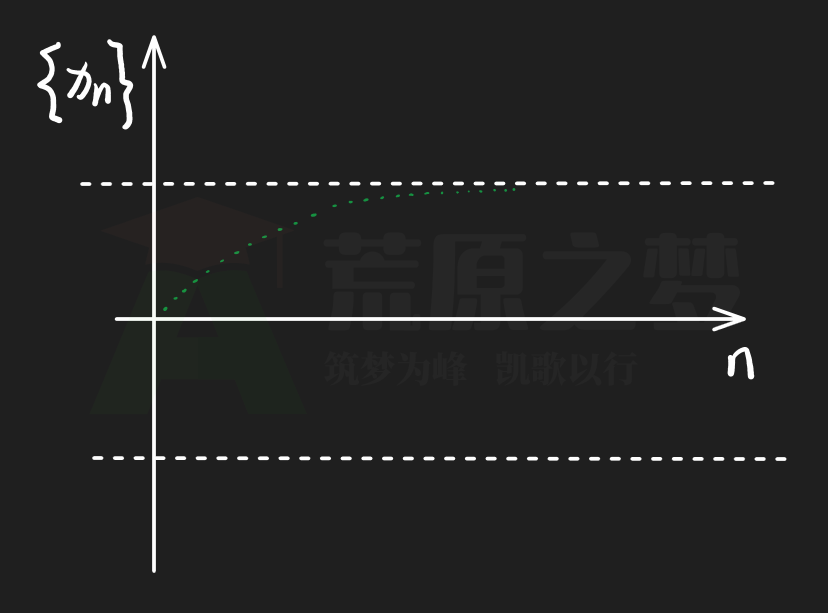
当然,下面这个数列虽然在 $n$ 比较小的时候没有收敛,但在 $n \rightarrow \infty$ 的时候,也是一个收敛数列:
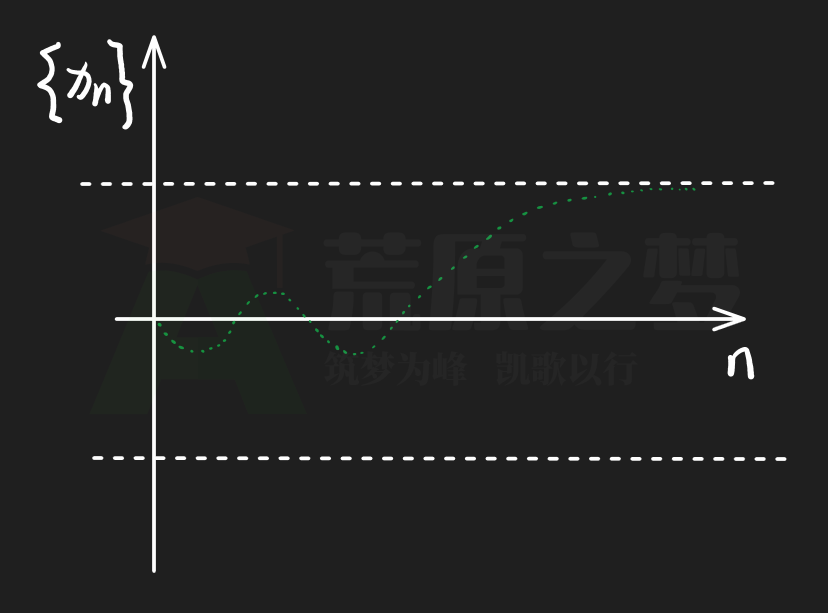
如果对数列的有界、发散、收敛有疑问的话,都可以看一看,理解一下上面的这些示意图,示意图的方式理解这些概念比定义或者特例更容易接受
高等数学
涵盖高等数学基础概念、解题技巧等内容,图文并茂,计算过程清晰严谨。
线性代数
以独特的视角解析线性代数,让繁复的知识变得直观明了。
特别专题
通过专题的形式对数学知识结构做必要的补充,使所学知识更加连贯坚实。