题目
编号:A2016221
已知函数 $f(x)$ 在 $[0, \frac{3 \pi}{2}]$ 上连续,在 $(0, \frac{3 \pi}{2})$ 内是函数 $\frac{\cos x}{2x – 3 \pi}$ 的一个原函数,且 $f(0) = 0$.
$(Ⅰ)$ 求 $f(x)$ 在区间 $[0, \frac{3 \pi}{2}]$ 上的平均值;
$(Ⅱ)$ 证明 $f(x)$ 在区间 $(0, \frac{3 \pi}{2})$ 内存在唯一零点.
解析
由题可得:
$$
f^{‘}(x) = \frac{\cos x}{2x – 3 \pi} \Rightarrow
$$
$$
f(x) = \int_{0}^{x} \frac{\cos t}{2t – 3 \pi} \mathrm{d} t.
$$
第 $(Ⅰ)$ 问
$f(x)$ 在区间 $[0, \frac{3 \pi}{2}]$ 上的平均值为:
$$
\frac{\int_{0}^{\frac{3 \pi}{2}} f(x) \mathrm{d} x}{\frac{3 \pi}{2} – 0} \Rightarrow
$$
$$
{\color{Red}\frac{2}{3 \pi} \int_{0}^{\frac{3 \pi}{2}} f(x) \mathrm{d} x} \quad {\color{White}①} \Rightarrow
$$
$$
\frac{2}{3 \pi}[ xf(x) |_{0}^{\frac{3 \pi}{2}} – \int_{0}^{\frac{3 \pi}{2}} xf^{‘} (x) \mathrm{d} x] \Rightarrow
$$
$$
\frac{2}{3 \pi}[ \frac{3 \pi}{2} f(\frac{3 \pi}{2}) – \int_{0}^{\frac{3 \pi}{2}} x \cdot \frac{\cos x}{2x – 3 \pi} \mathrm{d} x] \Rightarrow
$$
$$
\frac{2}{3 \pi}[ \frac{3 \pi}{2} \int_{0}^{\frac{3 \pi}{2}} \frac{ \cos x}{2x – 3 \pi} \mathrm{d} x – \int_{0}^{\frac{3 \pi}{2}} \frac{x \cos x}{2x – 3 \pi} \mathrm{d} x] \Rightarrow
$$
$$
\frac{2}{3 \pi}[ \int_{0}^{\frac{3 \pi}{2}} \frac{ \frac{3 \pi}{2} \cos x}{2x – 3 \pi} \mathrm{d} x – \int_{0}^{\frac{3 \pi}{2}} \frac{x \cos x}{2x – 3 \pi} \mathrm{d} x] \Rightarrow
$$
$$
\frac{2}{3 \pi}[ \frac{1}{2} \int_{0}^{\frac{3 \pi}{2}} \frac{ (3 \pi – 2x) \cos x}{2x – 3 \pi} \mathrm{d} x] \Rightarrow
$$
$$
\frac{2}{3 \pi}[ \frac{-1}{2} \int_{0}^{\frac{3 \pi}{2}} \frac{ (2x – 3 \pi) \cos x}{2x – 3 \pi} \mathrm{d} x] \Rightarrow
$$
$$
\frac{-1}{3 \pi}[\int_{0}^{\frac{3 \pi}{2}} \cos x \mathrm{d} x] \Rightarrow
$$
$$
\frac{-1}{3 \pi}[ \cos x |_{0}^{\frac{3 \pi}{2}}] \Rightarrow
$$
$$
\frac{-1}{3 \pi}[ -1-0 ] = \frac{1}{3 \pi}.
$$
当然,对于上面的 $①$ 式,还有一种计算方法:
$$
{\color{Red}\frac{2}{3 \pi} \int_{0}^{\frac{3 \pi}{2}} f(x) \mathrm{d} x} \Rightarrow
$$
$$
\frac{2}{3 \pi} \int_{0}^{\frac{3 \pi}{2}} \mathrm{d} x \int_{0}^{x} \frac{\cos t}{2t – 3 \pi} \mathrm{d} t \Rightarrow
$$
$$
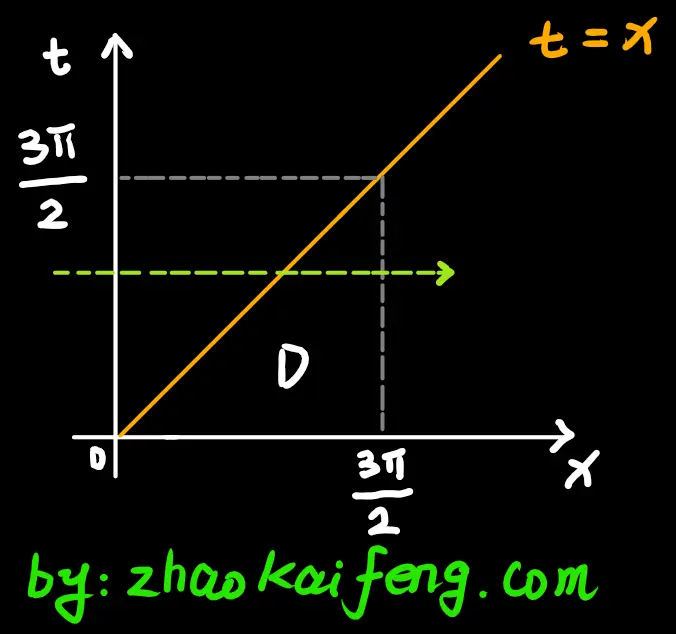
交换积分次序,交换方式如图 01 所示 \Rightarrow
$$
$$
\frac{2}{3 \pi} \int_{0}^{\frac{3 \pi}{2}} \frac{\cos t}{2t – 3 \pi} \mathrm{d} t \int_{t}^{\frac{3 \pi}{2}} \mathrm{d} x \Rightarrow
$$
$$
\frac{2}{3 \pi} \int_{0}^{\frac{3 \pi}{2}} \frac{\cos t}{2t – 3 \pi} \cdot (\frac{3 \pi}{2} – t) \mathrm{d} t \Rightarrow
$$
$$
\frac{2}{3 \pi} \cdot \frac{1}{2} \int_{0}^{\frac{3 \pi}{2}} \frac{\cos t}{2t – 3 \pi} \cdot (3 \pi – 2t) \mathrm{d} t \Rightarrow
$$
$$
\frac{-1}{3 \pi} \int_{0}^{\frac{3 \pi}{2}} \frac{\cos t}{2t – 3 \pi} \cdot (2t – 3 \pi) \mathrm{d} t \Rightarrow
$$
$$
\frac{-1}{3 \pi}[\int_{0}^{\frac{3 \pi}{2}} \cos t \mathrm{d} t] \Rightarrow
$$
$$
\frac{-1}{3 \pi}[ \cos t |_{0}^{\frac{3 \pi}{2}}] \Rightarrow
$$
$$
\frac{-1}{3 \pi}[ -1-0 ] = \frac{1}{3 \pi}.
$$
第 $(Ⅱ)$ 问
分析可知,要证明 $f(x)$ 在区间 $(0, \frac{3 \pi}{2})$ 内存在唯一零点,首先要证明“零点存在”,其次还要证明“零点唯一”。
由前述已知:
$$
f^{‘}(x) = \frac{\cos x}{2x – 3 \pi}.
$$
由于在 $(0, \frac{3 \pi}{2})$ 区间内,$2x – 3 \pi \leqslant 0$ 始终成立,于是,$f^{‘}(x)$ 的正负就可以通过 $\cos x$ 的正负进行判断:由 $\cos x$ 在区间 $(0, \frac{3 \pi}{2})$内的函数图像可知:
- 当 $x \in (0, \frac{\pi}{2})$ 时,$f^{‘}(x) < 0$, 即函数 $f(x)$ 在此区间内单调递减;
- 当 $x \in (\frac{\pi}{2}, \frac{3 \pi}{2})$ 时,$f^{‘}(x) > 0$, 即函数 $f(x)$ 在此区间内单调递增。
由于 $f(0) = 0$, 因此,函数 $f(x)$ 在区间 $(0, \frac{\pi}{2})$ 内始终不大于零,且 $f(\frac{\pi}{2}) < 0$.
又由第 $(Ⅰ)$ 问的计算结果,以及积分中值定理可知,一定有 $\xi \in (\frac{\pi}{2}, \frac{3 \pi}{2})$, 使得 $f(\xi) = \frac{1}{3 \pi} > 0$ 成立。
综上,在 $(\frac{\pi}{2}, \xi)$ 之间一定存在函数 $f(x)$ 的至少一个零点。而且,函数 $f(x)$ 在除了区间 $(\frac{\pi}{2}, \xi)$ 之外的其余定义域上不可能存在其他零点。
又由于函数 $f(x)$ 在区间 $(\frac{\pi}{2}, \frac{3 \pi}{2})$ 上是单调的,且 $(\frac{\pi}{2}, \xi) \in$ $(\frac{\pi}{2}, \frac{3 \pi}{2})$, 因此,函数 $f(x)$ 在区间 $(\frac{\pi}{2}, \xi)$ 上存在且唯一存在一个零点。