题目
设 $D$ 是由曲线 $y=x^{\frac{1}{3}}$, 直线 $x=a$ $(a>0)$ 及 $x$ 轴所围成的平面图形,$V_{x}$, $V_{y}$ 分别是 $D$ 绕 $x$ 轴,$y$ 轴旋转一周所得旋转体的体积,若 $V_{y} = 10V_{x}$, 求 $a$ 的值。
解析
首先,当 $x=0$ 时,对 $y=x^{\frac{1}{3}}$ 而言,$y=0$; 当 $x>0$ 时,对 $y=x^{\frac{1}{3}}$ 而言,$y>0$, 且 $x$ 的值越大,对应的 $y$ 的值也越大,据此,我们可以绘制出 $y=x^{\frac{1}{3}}$ 的大致图像,以及平面区域 $D$ 的大致形状。
函数 $y=x^{\frac{1}{3}}$ 在平面直角坐标系中的图像如图 01 所示:
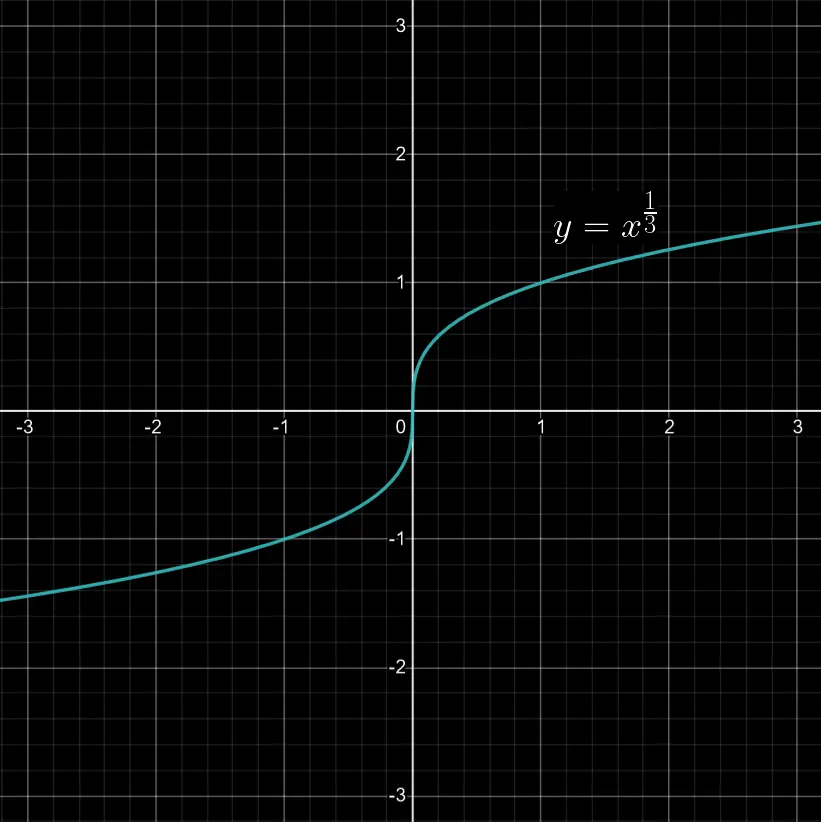
于是,由题可知:
$$
V_{x} = \pi \int_{0}^{a} (x^{\frac{1}{3}})^{2} dx.
$$
$$
V_{y} = 2 \pi \int_{0}^{a} x|x^{\frac{1}{3}}| dx.
$$
又:
$$
V_{y} = 10 V_{x}.
$$
于是:
$$
2 \pi \int_{0}^{a} x|x^{\frac{1}{3}}| dx = 10 \pi \int_{0}^{a} (x^{\frac{1}{3}})^{2} dx \Rightarrow
$$
$$
\int_{0}^{a} x(x^{\frac{1}{3}}) dx = 5 \int_{0}^{a} (x^{\frac{1}{3}})^{2} dx \Rightarrow
$$
$$
\int_{0}^{a} x^{\frac{4}{3}} dx = 5 \int_{0}^{a} x^{\frac{2}{3}} dx \Rightarrow
$$
$$
\frac{3}{7} x^{\frac{7}{3}} |_{0}^{a} = 5 \cdot \frac{3}{5} x^{\frac{5}{3}} |_{0}^{a} \Rightarrow
$$
$$
\frac{3}{7} x^{\frac{7}{3}} |_{0}^{a} = 3 x^{\frac{5}{3}} |_{0}^{a} \Rightarrow
$$
$$
\frac{3}{7} a^{\frac{7}{3}} = 3a^{\frac{5}{3}} \Rightarrow
$$
$$
a^{\frac{7}{3}} = 7a^{\frac{5}{3}} \Rightarrow
$$
$$
a^{\frac{5}{3}} \cdot a^{\frac{2}{3}} = 7 a^{\frac{5}{3}} \Rightarrow
$$
$$
a^{\frac{2}{3}} = 7 \Rightarrow
$$
$$
(a^{\frac{2}{3}})^{\frac{3}{2}} = 7^{\frac{3}{2}} \Rightarrow
$$
$$
a = 7^{\frac{3}{2}} \Rightarrow
$$
$$
a = \sqrt{7 \cdot 7 \cdot 7} \Rightarrow
$$
$$
a = 7\sqrt{7}.
$$