一、题目
设二维随机变量$(X,Y)$ 服从正态分布 $N(1,0;1,1;0),P\{XY-Y<0\}=$____.
二、解析
解答本题需要掌握正态分布和二维正态分布两部分知识。
1. 正态分布
正态分布通常用下面的公式表示:
$$X \sim N(\mu,\sigma^{2}).$$
其中 $\mu$ 表示数学期望(或称“均数”),$\sigma^{2}$ 表示方差,$\sigma$ 表示标准差。
参数 $\mu$ 决定了正态分布的分布图像在坐标系中的位置,正态分布的图像以 $x$ $=$ $\mu$ 为对称轴,左右完全对称。在正态分布中,数学期望 $=$ 均数 $=$ 中位数 $=$ 众数 $=$ $\mu.$
参数 $\sigma^{2}$ 决定了正态分布中随机变量的离散程度,$\sigma$ 越小,数据就越集中,反之,若 $\sigma$ 越大,数据就越集中。反应在正态分布的图像中就是,当 $\sigma$ 越小的时候,正态分布的图像越窄高,$\sigma$ 越大的时候,正态分布的图像越扁平。
正态分布的图像在 $(\mu – \sigma, \mu + \sigma)$ 区间内存在拐点,拐点附近的形状上表现为中间高两边低的特点。
特别地,$X \sim N(0,1)$ 为标准正态分布,其分布图象关于 $y$ 轴对称。
如图 1 是几种不同的正态分布图像,反映了参数 $\mu$ 和 $\sigma$ 对正态分布图像的影响,其中红色线表示的为标准正态分布:
2. 二维正态分布
二维正态分布可记作如下形式:
$(X,Y)$ $\sim$ $N(\mu_{1},\mu_{2};\sigma_{1}^{2},\sigma_{2}^{2};\rho).$
在本题中,需要用到关于二维正态分布的如下两个性质:
① $X$ $\sim$ $N(\mu_{1},\sigma_{1}^{2})$; $Y$ $\sim N(\mu_{2},\sigma_{2}^{2})$;
② $X$ 与 $Y$ 独立的充要条件是 $\rho=0.$ 我们可以使用如下 MATLAB 代码绘制二维正态分布条件概率密度函数图像:
x=-5:0.01:5;
y=-5:0.01:5;
mu=[-1,2];
sigma=[1 1; 1 3]; %输入均值向量和协方差矩阵,可以根据需要修改
[X,Y]=meshgrid(x,y); %产生网格数据并处理
p=mvnpdf([X(:),Y(:)],mu,sigma);
P=reshape(p,size(X)); %求取联合概率密度
figure(2)
surf(X,Y,P)
shading interp
colorbar
title('二维正态分布条件概率密度函数图像');
我在 MATLAB R2016b 上运行上述代码得到的二维正态分布条件概率密度函数图像如图 2 所示:
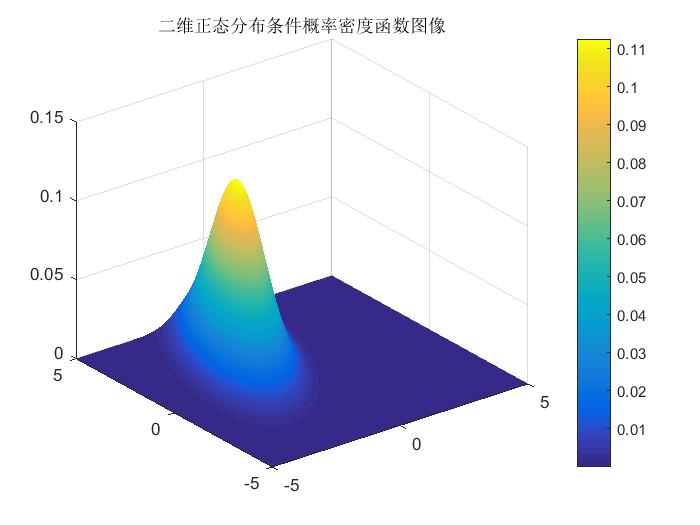
关于本题所用到的知识点的介绍就到这里结束,下面是具体的做题过程。
由题可知,$\rho=0,$ 因此,$X$ 与 $Y$ 相互独立,根据“随机变量的独立性”中的定理,我们知道,这也就意味着:
$$P\{X,Y\}=P\{X\}P\{Y\}.$$
于是,我们有:
$P\{XY-Y<0\}$ $=$ $P\{Y(X-1)<0\}$ $=$ $P\{Y>0,X-1<0\}$ $+$ $P\{Y<0,X-1>0\}$ $=$ $P\{Y>0,X<1\}+P\{Y<0,X>1\}$ $=$ $P\{Y>0\}P\{X<1\}$ $+$ $P\{Y<0\}P\{X>1\}$ $=$ $\frac{1}{2}$ $\times$ $\frac{1}{2}$ $+$ $\frac{1}{2}$ $\times$ $\frac{1}{2}$ $=$ $\frac{1}{2}.$
综上可知,本题的正确答案是:$\frac{1}{2}$
EOF