题目
设函数 $f(u)$ 二阶连续可导,$z=f(e^{x} \cos y)$ 满足 $\frac{\partial ^{2} z}{\partial x^{2}} + \frac{\partial ^{2} z}{\partial y^{2}}$ $=(4z + e^{x} \cos y)e^{2x}$, 若 $f(0)=0$, $f^{‘}(0)=0$, 求 $f(u)$ 的表达式.
继续阅读“2014年考研数二第18题解析:偏导数、二阶常系数非齐次线性微分方程”设函数 $f(u)$ 二阶连续可导,$z=f(e^{x} \cos y)$ 满足 $\frac{\partial ^{2} z}{\partial x^{2}} + \frac{\partial ^{2} z}{\partial y^{2}}$ $=(4z + e^{x} \cos y)e^{2x}$, 若 $f(0)=0$, $f^{‘}(0)=0$, 求 $f(u)$ 的表达式.
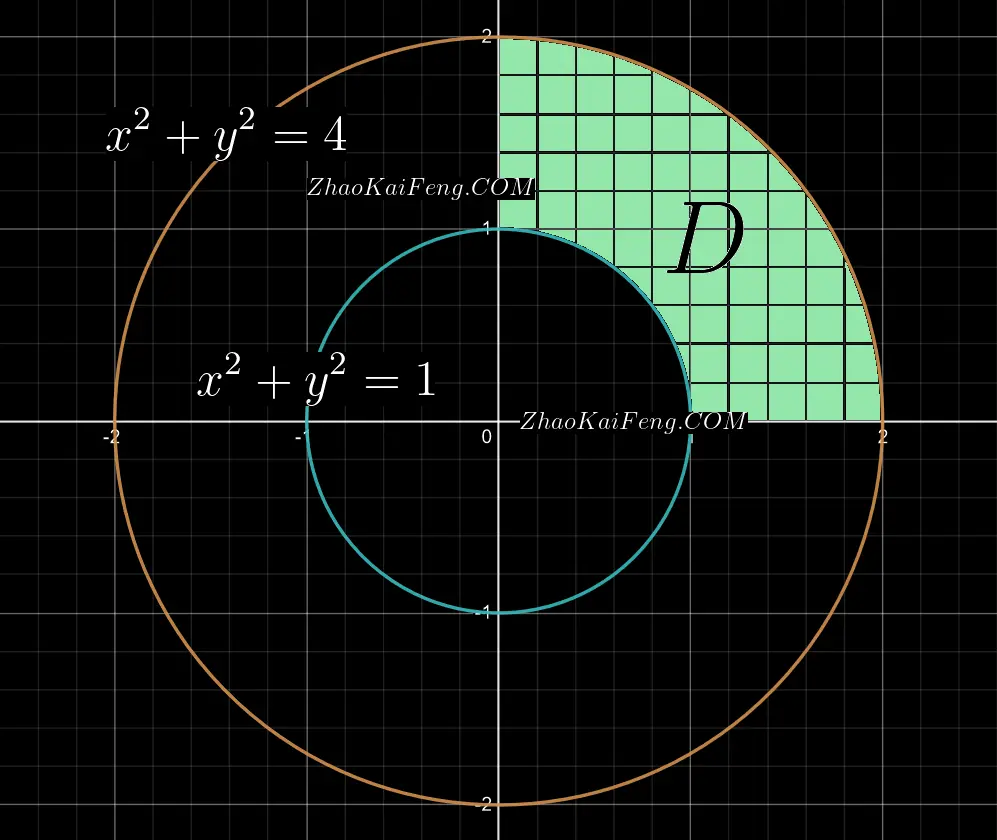
继续阅读“2014年考研数二第18题解析:偏导数、二阶常系数非齐次线性微分方程”设平面区域 $D=$ $\{(x,y)|$ $1 \leqslant x^{2} + y^{2} \leqslant 4$, $x \geqslant 0$, $y \geqslant 0 \}$, 计算:
$$
\iint_{D} \frac{x \sin (\pi \sqrt{x^{2}+y^{2}})}{x+y} dxdy.
$$
根据题目可知,积分区域 $D$ 是由两个圆心坐标均为 $(0,0)$, 半径分别为 $1$ 和 $2$ 的两个同心圆在直角坐标系的第一象限中围成的,如图 01 所示:
已知函数 $y=y(x)$ 满足微分方程 $x^{2}+y^{2}y^{‘} = 1-y^{‘}$, 且 $y(2)=0$, 求 $y=y(x)$ 的极大值与极小值.
继续阅读“2014年考研数二第16题解析:一阶线性微分方程求极值、求导”求极限:
$$
\lim_{x \rightarrow + \infty} \frac{ \int_{1}^{x}[t^{2}(e^{\frac{1}{t}}-1)-t] dt }{x^{2} \ln (1+\frac{1}{x})}.
$$
设二次型 $f(x_{1}, x_{2}, x_{3})=$ $2(a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3})^{2} +$ $(b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3})^{2}$,
记 $\alpha=\begin{bmatrix}
a_{1}\\
a_{2}\\
a_{3}
\end{bmatrix}$, $\beta=\begin{bmatrix}
b_{1}\\
b_{2}\\
b_{3}
\end{bmatrix}$,
$(Ⅰ)$ 证明:二次型 $f$ 对应的矩阵为 $2\alpha \alpha ^{\top}+\beta \beta ^{\top}$
$(Ⅱ)$ 若 $\alpha$, $\beta$ 正交且均为单位向量,证明:$f$ 在正交变换下的标准形为 $2y_{1}^{2}+y_{2}^{2}$.
继续阅读“2013年考研数二第23题解析:二次型、二次型的标准型”设 $A=\begin{bmatrix}
1 & a\\
1 & 0
\end{bmatrix}$, $B=\begin{bmatrix}
0 & 1\\
1 & b
\end{bmatrix}$,
当 $a$, $b$ 为何值时,存在矩阵 $C$ 使得 $AC-CA=B$, 并求所有矩阵 $C$.
继续阅读“2013年考研数二第22题解析:矩阵、非齐次线性方程组求解”设曲线 $L$ 的方程为 $y=\frac{1}{4} x^{2} – \frac{1}{2} \ln x$ $(1 \leqslant x \leqslant e)$.
$(Ⅰ)$ 求 $L$ 的弧长;
$(Ⅱ)$ 设 $D$ 是由曲线 $L$, 直线 $x=1$, $x=e$ 及 $x$ 轴所围平面图形,求 $D$ 的形心的横坐标.
继续阅读“2013年考研数二第21题解析:平面曲线的弧长、平面图形的形心”设函数 $f(x)=\ln x + \frac{1}{x}$.
$(Ⅰ)$ 求 $f(x)$ 的最小值;
$(Ⅱ)$ 设数列 ${x_{n}}$ 满足 $\ln x_{n} + \frac{1}{x_{n+1}}<1$. 证明 $\lim_{n \rightarrow \infty} x_{n}$ 存在,并求此极限。
继续阅读“2013年考研数二第20题解析:导数与最值、数列极限的判定与求解”求曲线 $x^{3}-xy+y^{3}=1$ $(x \geqslant 0, y \geqslant 0)$ 上的点到坐标原点的最长距离与最短距离。
继续阅读“2013年考研数二第19题解析:拉格朗日乘数法求条件极值、求曲线上的最值”设奇函数 $f(x)$ 在 $[-1,1]$ 上具有二阶导数,且 $f(1)=1$. 证明:
$(Ⅰ)$ 存在 $\xi \in (0,1)$, 使得 $f^{‘}(\xi)=1$;
$(Ⅱ)$ 存在 $\eta \in (-1,1)$, 使得 $f^{”}(\eta) + f^{‘}(\eta)=1$.
继续阅读“2013年考研数二第18题解析:拉格朗日中值定理、罗尔定理、中值定理”设平面区域 $D$ 由直线 $x=3y$, $y=3x$ 与 $x+y=8$ 围成。计算 $\iint_{D} x^{2} dxdy.$
继续阅读“2013年考研数二第17题解析:二重积分的计算”设 $D$ 是由曲线 $y=x^{\frac{1}{3}}$, 直线 $x=a$ $(a>0)$ 及 $x$ 轴所围成的平面图形,$V_{x}$, $V_{y}$ 分别是 $D$ 绕 $x$ 轴,$y$ 轴旋转一周所得旋转体的体积,若 $V_{y} = 10V_{x}$, 求 $a$ 的值。
继续阅读“2013年考研数二第16题解析:计算旋转体的体积”当 $x \rightarrow 0$ 时,$1-\cos x \cdot \cos 2x \cdot \cos 3x$ 与 $ax^{n}$ 为等价无穷小,求 $n$ 与 $a$ 的值。
继续阅读“2013年考研数二第15题解析:等价无穷小”已知:
$$
A =
\begin{bmatrix}
1 & 0 & 1\\
0 & 1 & 1\\
-1 & 0 & a\\
0 & a & -1
\end{bmatrix},
$$
二次型 $f(x_{1}, x_{2}, x_{3})=X^{\top}(A^{\top}A)X$ 的秩为 $2$.
$(Ⅰ)$ 求实数 $a$ 的值;
$(Ⅱ)$ 求正交变换 $x=Qy$, 将 $f$ 化为标准形。
继续阅读“2012年考研数二第23题解析:二次型基础、二次型化为标准型、秩”设:
$$
A=\begin{bmatrix}
1 & a & 0 & 0\\
0 & 1 & a & 0\\
0 & 0 & 1 & a\\
a & 0 & 0 & 1
\end{bmatrix},
$$
$$
\beta=
\begin{bmatrix}
1\\
-1\\
0\\
0
\end{bmatrix}.
$$
$(Ⅰ)$ 计算行列式 $|A|$.
$(Ⅱ)$ 当实数 $a$ 为何值时,方程组 $AX=\beta$ 有无穷多解,并求其通解。
继续阅读“2012年考研数二第22题解析:行列式的按行(列)展开定理、非齐次线性方程组求解”