2019 年 10 月 25 日是苹果公司联合创始人之一 Steven Paul Jobs 逝世八周年纪念日。这一天,Apple 现任 CEO Tim Cook 发了一条推文:“我们所拥有的最珍贵的资源是时间,乔布斯,我们永远怀念你。”

Steve Jobs at the 2010 Worldwide Developers Conference:

EOF
2019 年 10 月 25 日是苹果公司联合创始人之一 Steven Paul Jobs 逝世八周年纪念日。这一天,Apple 现任 CEO Tim Cook 发了一条推文:“我们所拥有的最珍贵的资源是时间,乔布斯,我们永远怀念你。”

Steve Jobs at the 2010 Worldwide Developers Conference:

EOF
今天是祖国的生日,一个普天同庆的日子,一个属于所有中华儿女的日子。
近代历史上,中华民族被压迫被凌辱得太久了,以至于每当遇到这样的时刻,总会让人热泪盈眶,激动不已。今天的中华大地上处处洋溢着欢乐,这是一种略带悲情的欢乐——多少人的牺牲与付出才有了我们今天的一切,为了今天,我们民族经历了太多的苦难。
如今的中国,有现代化的军队,有日新月异的科技,有饱含斗志的人民,这是实现中国梦最好的时候,也是我们离中华复兴最近的时候。
一位位先烈为了民族独立,为了国家富强,前赴后继,舍生忘死。今天的我们更应该努力奋进,以一往无前的干劲儿托举出共和国更加美好的明天。
加油吧,一万年太久,只争朝夕!
2019 年 09 月 17 日,CentOS 官方在 Twitter 上发布消息称,下一个版本的 CentOS 将于 09 月 24 日在所有例行平台发布,如图 1:
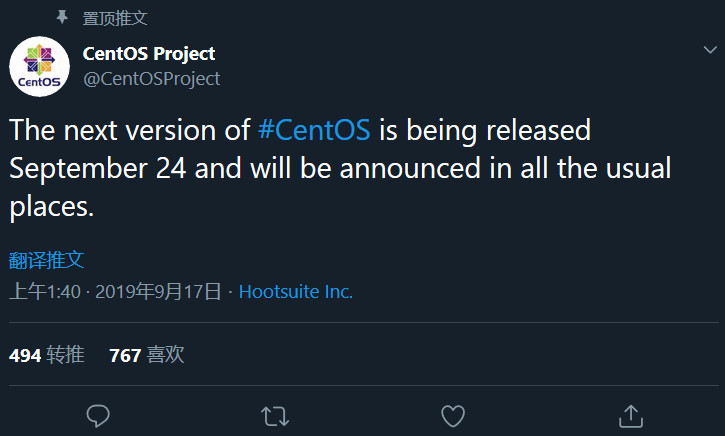
此外,CentOS 8 的当前进度时间表也更新了,最新的信息显示,CentOS 8 将于 2019 年 09 月 24 日发行:
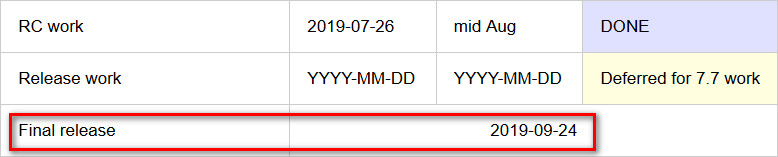
EOF
CentOS 8 Current Timeline:
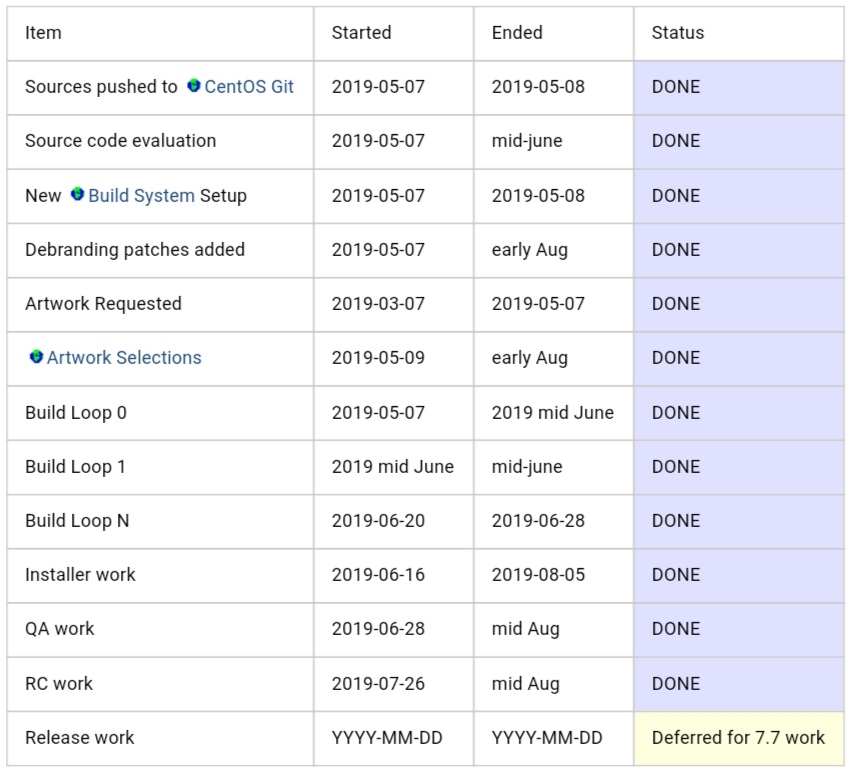
CentOS 于 2019 年 09 月 12 日在其官网更新了一条关于 CentOS 8 的 Updates, 原文如下:
2019-09-10 According to this thread, work was stopped on CentOS 8 after upstream released 7.7. Since so many more users have CentOS 7.x in production, and no one has 8 yet, priority has been given to the 7.7 update… and once it is done, work will continue on 8.
https://wiki.centos.org/About/Building_8
参考译文如下:
根据计划,CentOS 8 的相关工作将会暂停,直到完成 CentOS 7.7 的版本发行工作。因为有许多用户在生产环境中使用了 CentOS 7.x, 但还没有用户使用 CentOS 8, 于是,对 CentOS 7.7 的更新具有更高的优先级。一旦 CentOS 7.7 的工作完成,CentOS 8 的工作就将继续进行。
EOF
声明:本文所阐述的观点仅供参考,本文所得出的结论仅仅是思想实验的可能结果,没有经过实验验证。
观看和“吃”相关的视频的时候,可能会因人体的条件反射导致胃酸分泌量增加,然而这个时候人们可能并没有真正进食。再加上深夜的时候,距离吃完晚饭已经有一段时间,胃部的食物已经快要消化完毕,这个时候如果再有较多的胃酸分泌,就有可能诱发或者加重胃部疾病。
根据 Google 博客的消息(原文地址:https://www.blog.google/products/android/evolving-android-brand/),包括手机,汽车,手表,电视等设备在内,全球范围内搭载 Android 系统的设备已经超过 25 亿台。为了使 Android 发展得更好,Google 方面最近采取了两项措施。
在之前的发行版中,Google 的工程师会给每个发行版起一个内部代码名字,这个名字通常是按首字母顺序依次使用的美味的点心或者甜品的名称。这么做虽然很有趣,但是根据过去几年的反馈,并不是每个人都能理解这些名字的含义,因为 Android 在世界各个地方都有开发者,这些开发者之间有着许多语言和文化上的差异。例如,在一些语言中是不区分 “L” 和 “R” 的,因此,习惯于使用这些语言的人们就不能直观地理解 “Android Lollipop” 是 “Android KitKat” 之后的一个版本。同样的困扰也可能存在于 Android 的使用者身上,由于有些用户可能不了解 Android 的命名惯例,因此就难以判断自己的设备上运行的 Android 系统是不是最新版的。此外,在一些地方,”pies” 并不是指的甜点,而且虽然棉花糖 (marshmallows) 很美味,但并不是世界上所有地方都流行吃棉花糖。
作为一个全球性的操作系统,对人们来说,一个清晰直观的名字是很重要的。因此,从下一个版本的 Android 系统开始,将使用简单直接的数字来命名,而下一个版本的 Android 被命名为 “Android 10”.

Android 系统的 LOGO 已经变化了很多次了,此次对 LOGO 的修改更多地考虑到使其更加“无障碍化”,因为对于 Android 开发者社区中一些有视觉障碍的人们而言,绿色的图标可能比较难以分辨。于是 Google 这次将 LOGO 中的 “Android” 变成了黑色的。
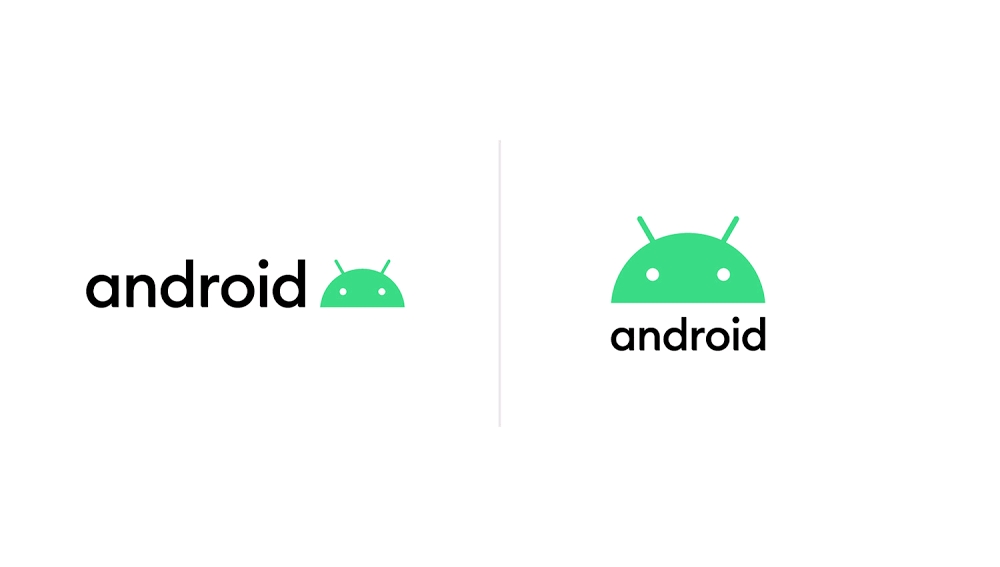
EOF
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $(\frac{\sin x}{1+\cos x}$ $+$ $|x|)$ $dx$ $=$__.
本题存在(关于原点对称的)对称区间 “$[-\frac{\pi}{2}$, $\frac{\pi}{2}]$”, 在求积分的时候,如果看到这样的对称区间,则要考虑被积函数是不是奇函数或者偶函数。如果是奇函数,则其在对称区间上的积分为 $0$, 如果是偶函数,则我们可以只计算其大于 $0$ 或者小于 $0$ 方向上的积分,之后再乘以 $2$ 即可获得整个积分区间上的积分数值。
由于:
$\frac{\sin (-x)}{1+\cos(-x)}$ $=$ $\frac{-\sin x}{1+\cos x}$ $\Rightarrow$ $f(-x)$ $=$ $-f(x)$.
因此,$f(x)$ $=$ $\frac{\sin x}{1+\cos x}$ 是一个奇函数,因此,其在对称区间 $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$ 上的积分为 $0$.
又由于:
$|-x|$ $=$ $|x|$ $\Rightarrow$ $g(-x)$ $=$ $g(x)$.
因此,$g(x)$ $=$ $|x|$ 是一个偶函数。
于是:
原式 $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $|x|$ $dx$ $=$ $2$ $\int_{0}^{\frac{\pi}{2}}$ $x$ $dx$ $=$ $2$ $\cdot$ $\frac{1}{2}x^{2}|_{0}^{\frac{\pi}{2}}$ $=$ $\frac{\pi^{2}}{4}$.
当然,本题除了可以使用积分的原理计算之外,还可以画图计算面积,如图 1:
根据上图,我们有:
$\frac{\pi}{2}$ $\cdot$ $\frac{\pi}{2}$ $\cdot$ $\frac{1}{2}$ $\cdot$ $2$ $=$ $\frac{\pi^{2}}{4}$.
综上可知,本题的正确答案是:$\frac{\pi^{2}}{4}$.
EOF
$\lim_{x \rightarrow 0}$ $(\frac{1-\tan x}{1+\tan x})^{\frac{1}{\sin kx}}$ $=$ $e$, 则 $k$ $=$__.
观察本题可以发现,这是一个求极限的式子,而且等式的右边是 $e$, 符合“两个重要极限”中的第二个重要极限的一部分特征。
两个重要极限如下:
$\lim_{x \rightarrow x_{x_{0}}}$ $\frac{\sin x}{x}$ $=$ $1$, $\lim_{x \rightarrow 0}$ $(1+x)^{\frac{1}{x}}$ $=$ $\lim_{x \rightarrow \infty}$ $(1+\frac{1}{x})^{x}$ $=$ $e$.
由于题目中的式子不存在上述公式中的 $1$, 因此,我们需要构造出这个 $1$, 即:
$1$ $+$ $\square$ $=$ $\frac{1-\tan x}{1+\tan x }$ $\Rightarrow$ $\square$ $=$ $\frac{1-\tan x}{1+\tan x}$ $-$ $1$ $=$ $\frac{1-\tan x}{1+\tan x}$ $-$ $\frac{1+\tan x}{1+\tan x}$ $=$ $\frac{-2 \tan x}{1+\tan x}$.
于是,原式 $=$ $\lim_{x \rightarrow 0}$ $(1+\frac{-2\tan x}{1+\tan x})^{\frac{1}{\sin kx}}$ $=$ $e$. (1)
由于当 $x$ $\rightarrow$ $0$ 时,$\frac{-2\tan x}{1+\tan x}$ $\rightarrow$ $0$ 且 $\frac{1}{\sin kx}$ $\rightarrow$ $\infty$, 所以,符合使用“两个重要极限”的条件,可以继续接下来的计算。
接下来继续向公式的方向构造等式。
$(1)$ $=$ $\lim_{x \rightarrow 0}$ $(1+\frac{-2\tan x}{1+\tan x})^{\frac{1+\tan x}{-2\tan x} \frac{-2\tan x}{1+\tan x} \frac{1}{\sin kx}}$. (2)
根据公式,我们知道:
$\lim_{x \rightarrow 0}$ $(1+\frac{-2\tan x}{1+\tan x})^{\frac{1+\tan x}{-2\tan x}}$ $=$ $e$.
于是:
$(2)$ $=$ $e^{\lim_{x \rightarrow 0} \frac{-2\tan x}{1+\tan x}\frac{1}{\sin kx}}$ $=$ $e^{\lim_{x \rightarrow 0} \frac{-2\tan x}{(1+\tan x)\sin kx}}$. (3)
当 $x$ $\rightarrow$ $0$ 时,$\tan x$ $\rightarrow$ $0$ 是不可以带入原式中的(只有非零和非无穷的数值可以带入原式中。),不过当 $x$ $\rightarrow$ $0$ 时,$(1+\tan x)$ $\rightarrow$ $1$ 是可以带入原式中的,于是:
$\lim_{x \rightarrow 0}$ $\frac{-2\tan x}{(1+\tan x)\sin kx}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{-2\tan x}{\sin kx}$.
又因为当 $x$ $\rightarrow$ $0$ 时,$\sin x$ $\sim$ $\tan x$ $\sim x$, 于是:
$\lim_{x \rightarrow 0}$ $\frac{-2\tan x}{\sin kx}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{-2x}{kx}$ $=$ $-\frac{2}{k}$.
即:
$e^{-\frac{2}{k}}$ $=$ $e$ $\Rightarrow$ $-$ $\frac{2}{k}$ $=$ $1$ $\Rightarrow$ $k$ $=$ $-$ $2$.
综上可知,正确答案是:$-2$.
EOF
设函数 $f(x)$ $=$ $x$ $+$ $a$ $\ln(1+x)$ $+$ $bx$ $\sin x$, $g(x)$ $=$ $k$ $x^{3}$ 在 $x$ $\rightarrow$ $0$ 时等价无穷小,求常数 $a$, $b$, $k$ 的取值.
由于 $x$ $\rightarrow$ $0$ 时,$f(x)$ 和 $g(x)$ 是等价无穷小,因此有:
$\lim_{x \rightarrow 0}$ $\frac{f(x)}{g(x)}$ $=$ $1$, 即:
$\lim_{x \rightarrow 0}$ $\frac{x+a \ln(1+x) + bx \sin x}{kx^{3}}$ $=$ $1$.
又由麦克劳林公式:
1. $\sin x$ $=$ $x$ $+$ $o(x^{2})$;
注 1:
根据麦克劳林公式,$\sin x$ 也可以等于 $x$ $-$ $\frac{x^{3}}{6}$ $+$ $o(x^{4})$, 但是这里为了能够在接下来的计算中使得分子分母可以使用“对照”的方式求解,分子的最大幂次不能大于分母的最大幂次。由于 $\sin x$ 在使用麦克劳林公式替换之后还需要和 $x$ 相乘得到二次幂,因此这里只能令 $\sin x$ 等于 $x$ $+$ $o(x^{2})$.
2. $\ln(1+x)$ $=$ $x$ $-$ $\frac{x^{2}}{2}+\frac{x^{3}}{3}$ $+$ $o(x^{3})$.
注 2:
对 $\ln(1+x)$ 项数的选取所依据的原因和注 $1$ 一致。
于是,我们有:
$1$ $=$ $\lim_{x \rightarrow 0}$ $\frac{x+ax-\frac{a}{2}x^{2}+\frac{a}{3}x^{3}+o(x^{3})+bx^{2}+o(x^{3})}{kx^{3}}$ $=$ $\lim_{x \rightarrow 0}$ $\frac{(1+a)x+(b-\frac{a}{2})x^{2}+\frac{a}{3}x^{3}+o(x^{3})}{kx^{3}}$.
于是,我们有:
$\left\{\begin{matrix} 1+a=0,\\ b-\frac{a}{2}=0,\\ \frac{a}{3}=k. \end{matrix}\right.$
解得:
$\left\{\begin{matrix} a=-1,\\ b=-\frac{1}{2},\\ k=-\frac{1}{3}. \end{matrix}\right.$

EOF

如果从 1969 年 NASA 的航天器成功登陆月球开始算起,今年是阿波罗计划 50 周年。
在 1971 年的 07 月 31 日,阿波罗 15 号任务首次在月球使用了月球漫游车。这是一台轻量级的车,使用电力驱动,可以在月球表面的低重力真空环境中行驶,帮助宇航员探索着陆点周围的环境。
本文中的这张照片是在阿波罗 15 号任务中宇航员第三次出舱活动时拍摄的,照片的背景是荒凉的月球和无穷无尽的深空。然而,当人类的脚步开始点缀在这颗星球上时,她的美便开始难以用语言形容。
更多信息可以访问:
https://www.nasa.gov/centers/marshall/history/index.html
微分方程 $y”$ $+$ $2y’$ $+$ $3y$ $=$ $0$ 的通解为__.
观察可知,这是一个二阶常系数线性齐次微分方程。
二阶常系数线性齐次微分方程的性质如下:
形如 $y”$ $+$ $py’$ $+$ $qy$ $=$ $0$, 其中 $p$, $q$ 均为常数。
特征方程为:$\lambda^{2}$ $+$ $p$ $\lambda$ $+$ $q$ $=$ $0$,
(1) 当 $\lambda_{1}$, $\lambda_{2}$ 为互异实根时,微分方程得通解为 $y(x)$ $=$ $C_{1}$ $e^{\lambda_{1}x}$ $+$ $C_{2}$ $e^{\lambda_{2}x}$;
(2) 当 $\lambda_{1}$ $=$ $\lambda_{2}$ 时,通解为 $y(x)$ $=$ $(C_{1}+C_{2}x)$ $e^{\lambda_{1}x}$;
(3) 当 $\lambda$ $=$ $\alpha$ $\pm$ $i$ $\beta$ (复数根)时,通解为 $y(x)$ $=$ $e^{\alpha x}$ $(C_{1}$ $\cos \beta$ $x$ $+$ $C_{2}$ $\sin \beta$ $x)$.
在本题中,特征方程中的 $p$ $=$ $2$, $q$ $=$ $3$, 因此特征方程为:
$\lambda^{2}$ $+$ $2$ $\lambda$ $+$ $3$ $=$ $0$. (1)
此外,我们还知道,对于形如 $a$ $x^{2}$ $+$ $bx$ $+$ $c$ $=0$ 的一元二次方程,其求根公式为:
$x$ $=$ $\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$.
于是,我们知道,对于 (1) 式:
$\lambda$ $=$ $\frac{-2\pm\sqrt{4-12}}{2}$ $=$ $\frac{-2\pm\sqrt{-8}}{2}$. (2)
我们又知道,在虚数中(复数包含虚数和实数),虚数单位 $i$ 有如下性质:
$i^{2}$ $=$ $-1$.
于是,(2) 式可以写成:
$\lambda$ $=$ $\frac{-2\pm\sqrt{8i^{2}}}{2}$ $=$ $\frac{-2\pm i 2 \sqrt{2}}{2}$ $=$ $-1$ $\pm$ $i$ $\sqrt{2}$.
于是,$\alpha$ $=$ $-1$, $\beta$ $=$ $\sqrt{2}$.
因此,正确答案是:
$y$ $=$ $e^{-x}$ $(C_{1}$ $\cos \sqrt{2}x$ $+$ $C_{2}$ $\sin \sqrt{2}$ $x$ $)$
EOF
微分方程 $xy’$ $+$ $y$ $=0$ 满足条件 $y(1)$ $=$ $1$ 的解是 $y$ $=$__.
由 $xy’$ $+$ $y$ $=0$ 得:
$(xy)’$ $=0$.
即:
$xy$ $=$ $C$ $\Rightarrow$ $y$ $=$ $\frac{C}{x}$
又因为 $y(1)$ $=$ $1$ $\Rightarrow$ $1$ $=$ $\frac{C}{1}$ $\Rightarrow$ $C$ $=$ $1$ $\Rightarrow$ $y$ $=$ $\frac{1}{x}$.
综上可知,正确答案是:$\frac{1}{x}$.
EOF
设有两个数列 ${a_{n}}$, ${b_{n}}$, 若 $\lim_{n \rightarrow \infty}$ $a_{n}$ $=0$, 则()
( A ) 当 $\sum_{n=1}^{\infty}$ $b_{n}$ 收敛时,$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ 收敛.
( B ) 当 $\sum_{n=1}^{\infty}$ $b_{n}$ 发散时,$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ 发散.
( C ) 当 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 收敛时,$\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ 收敛.
( D ) 当 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 发散时,$\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ 发散.
由题目信息可知,当 $n$ $\rightarrow$ $\infty$ 时,数列 ${a_{n}}$ 是收敛的。
A 项:
令 $a_{n}$ $=$ $b_{n}$ $=$ $(-1)^{n-1}$ $\frac{1}{\sqrt{n}}$.
则此时 ${a_{n}}$ 是一个收敛数列,$\sum_{n=1}^{\infty}$ $b_{n}$ 也收敛(根据交错级数的莱布尼茨准则判别法可得此结论),但 $\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n}$ 发散(由常见级数的敛散性可得此结论)。
由此构成了对 A 项的反例,A 项错误。
注 1. 交错级数 $\sum_{n=1}^{\infty}$ $(-1)^{n-1}u_{n}$ $(u_{n}>0)$ 的判别法(莱布尼茨准则):
若交错级数 $\sum_{n=1}^{\infty}$ $(-1)^{n-1}u_{n}$ $(u_{n}>0)$ 满足如下条件:
① $u_{n}$ $\geqslant$ $u_{n+1}$, $(n = 1,2,3, \dotsc)$;
② $\lim$ $u_{n}$ $=$ $0$,
则交错级数收敛,其和 $S$ $\leqslant$ $u_{1}$, 余项 $|R_{n}|$ $\leqslant$ $u_{n+1}$.
注 2. 常见级数的敛散性:
$p$ 级数 $\sum_{n=1}^{\infty}$ $\frac{1}{n^{p}}$ $\left\{\begin{matrix} 收敛 & p>1,\\ 发散 & p \leqslant 1. \end{matrix}\right.$
B 项:
令 $a_{n}$ $=$ $b_{n}$ $=$ $\frac{1}{n}$, 则
$\sum_{n=1}^{\infty}$ $a_{n}$ $b_{n}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n^{2}}$.
此时,数列 ${a_{n}}$ 是一个收敛数列,$\sum_{n=1}^{\infty}$ $b_{n}$ 是发散的,但是 $\sum_{n=1}^{\infty}$ $\frac{1}{n^{2}}$ 是收敛的。
由此构成了对 B 项的反例,B 项错误。
D 项:
和 B 项一样,令 $a_{n}$ $=$ $b_{n}$ $=$ $\frac{1}{n}$, 则 $\sum_{n=1}^{\infty}$ $a_{n}^{2}$ $b_{n}^{2}$ $=$ $\sum_{n=1}^{\infty}$ $\frac{1}{n^{4}}$ 是收敛的。
由此构成了对 D 项的反例,D 项错误。
综上可知,排除了 A, B, D 三个选项后,正确选项一定是 C 项。
我们可以使用级数收敛的必要条件直接证明 C 项正确。
级数 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛的必要条件:$\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$.
由于 $\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$ 是级数 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛的必要条件,因此,根据“小充分大必要”的原则,我们知道:
$\sum_{n=1}^{\infty}$ $u_{n}$ 收敛 $\Rightarrow$ $\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$;
$\lim_{n \rightarrow \infty}$ $u_{n}$ $=$ $0$ $\nRightarrow$ $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛。
由于 $\lim_{n \rightarrow \infty}$ $a_{n}$ $=$ $0$, 从而存在 $M$ $>$ $0$, 有 $|a_{n}|$ $\leqslant$ $M$, 即:
$a_{n}^{2}$ $b_{n}^{2}$ $\leqslant$ $M^{2}$ $b_{n}^{2}$. 又因为 $\sum_{n=1}^{\infty}$ $|b_{n}|$ 收敛,故有:
$\lim_{n \rightarrow \infty}$ $|b_{n}|$ $=0$.
又根据如下定理:
设 $c$ 为非零常数,则 $\sum_{n=1}^{\infty}$ $u_{n}$ 与 $\sum_{n=1}^{\infty}$ $cu_{n}$ 具有相同的敛散性。
因此,$\sum_{n=1}^{\infty}$ $M^{2}$ $|b_{n}|$ 收敛,即:
$\lim_{n=1}^{\infty}$ $M^{2}$ $|b_{n}|$ $=$ $0$.
于是:
$\lim_{n \rightarrow \infty}$ $\frac{M^{2}|b_{n}||b_{n}|}{|b_{n}|}$ $=$ $\lim_{n \rightarrow \infty}$ $M^{2}$ $|b_{n}|$ $=$ $\lim_{n \rightarrow \infty}$ $\frac{M^{2}b_{n}^{2}}{|b_{n}|}$ $=$ $0$.
接下来,根据“比较判别法的极限形式”:
设 $\sum_{n=1}^{\infty}$ $u_{n}$ 与 $\sum_{n=1}^{\infty}$ $v_{n}$ 均为正项级数,且 $\lim_{n \rightarrow \infty}$ $\frac{u_{n}}{v_{n}}$ $=$ $A(v_{n} \neq 0)$.
① 若 $0$ $\leqslant$ $A$ $\leqslant$ $+$ $\infty$, 且 $\sum_{n=1}^{\infty}$ $v_{n}$ 收敛,则 $\sum_{n=1}^{\infty}$ $u_{n}$ 收敛.
② 若 $0$ $\leqslant$ $A$ $\leqslant$ $+$ $\infty$, 且 $\sum_{n=1}^{\infty}$ $v_{n}$ 发散,则 $\sum_{n=1}^{\infty}$ $u_{n}$ 发散.
于是我们知道,$\sum_{n=1}^{\infty}$ ${M^{2} b_{n}^{2}}$ 收敛。
又因为 $a^{2}$ $b^{2}$ $\leqslant$ $M^{2}$ $b^{2}$, 所以:
$\sum_{n=1}^{\infty}$ ${a^{2} b_{n}^{2}}$ 收敛.
由此得证 C 项正确。
EOF
设 $M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{(1+x)^{2}}{1+x^{2}}$ $dx$, $N$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{1+x}{e^{x}}$ $dx$, $K$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $(1+\sqrt{\cos x})$ $dx$, 则 ( )
( A ) $M$ $>$ $N$ $>$ $K$
( B ) $M$ $>$ $K$ $>$ $N$
( C ) $K$ $>$ $M$ $>$ $N$
( D ) $K$ $>$ $N$ $>$ $M$
在解答题目时,能化简的要先化简,能计算出具体数值的要先计算出具体数值。
首先观察本题,发现 $M$ 对应的式子应该是可以化简或者通过积分计算出具体的数值。于是:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{(1+x)^{2}}{1+x^{2}}$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{1+x^{2}+2x}{1+x^{2}}$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $[\frac{1+x^{2}}{1+x^{2}}$ $+$ $\frac{2x}{1+x^{2}}]$ $dx$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $[$ $1$ $+$ $\frac{2x}{1+x^{2}}]$ $dx$
计算到上面这一步之后,我们有两种方法可以继续上面的计算,一种方法是利用积分函数在对称区间上的性质,另一种是利用基本积分公式直接计算。
下面分别使用上述提到的两种方法展开计算。
方法一:利用积分函数在对称区间上的性质
这里说的“对称区间”指的是关于原点对称的区间,观察题目可知,题目中的积分函数的上限和下限组成的区间 $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$ 正好是关于原点对称的。
根据积分的几何意义,我们知道,奇函数在关于原点对称的对称区间上的积分是等于 $0$ 的。
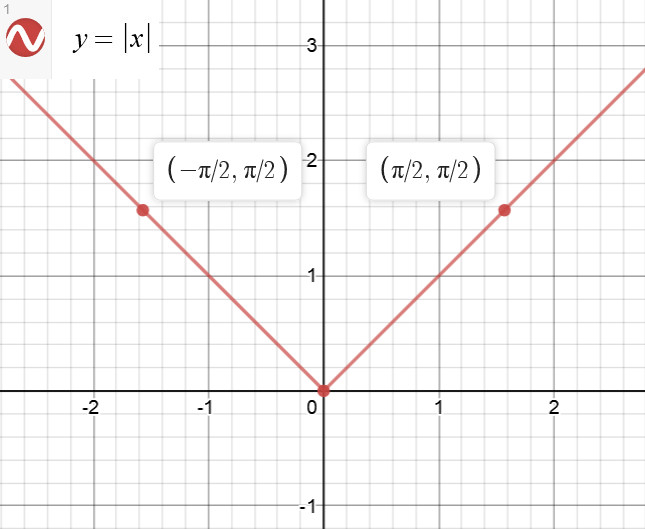
$y$ $=$ $x$, $x$ $\in$ $(-\infty,$ $+\infty)$ 就是一个典型的奇函数,如图 1:
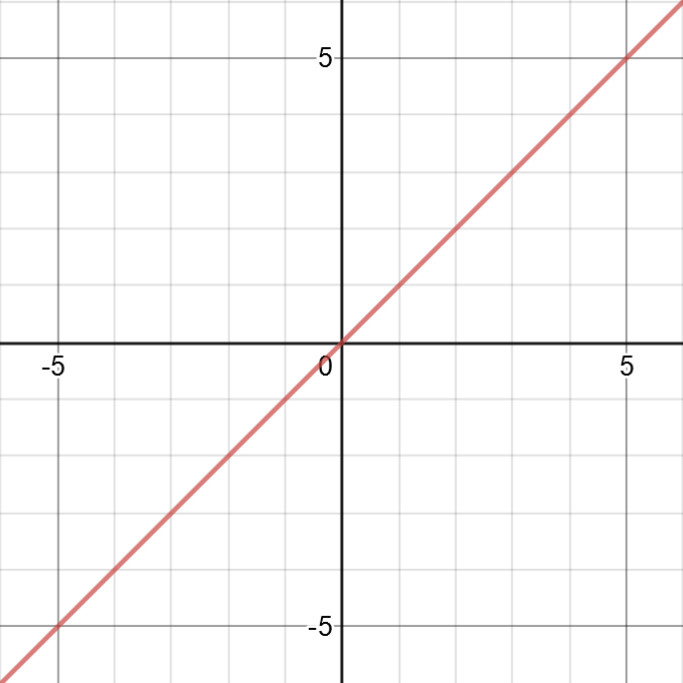
因此,接下来,我们如果能证明一个函数是奇函数,就可以证明这个函数在关于原点对称的区间上的积分是 $0$.
于是,令:
$f(x)$ $=$ $\frac{2x}{1+x^{2}}$
则:
$\frac{2(-x)}{1+(-x)^{2}}$ $=$ $-\frac{2x}{1+x^{2}}$ $\Rightarrow$ $f(-x)$ $=$ $-f(x)$.
因此 $f(x)$ $=$ $\frac{2x}{1+x^{2}}$ 是一个奇函数,于是:
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{2x}{1+x^{2}}$ $dx$ $=$ $0$.
即:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$.
方法二:利用基本积分公式直接计算
由前面的计算,我们已知,$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $\frac{2x}{1+x^{2}}$ $dx$, 于是,根据积分公式:
$d(x^{\mu})$ $=$ $\mu$ $x^{\mu-1}$ $dx$
我们可以令 $2x$ $dx$ $=$ $d(1+x^{2})$.
于是:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$ $+$ $\frac{d(1+x^{2})}{1+x^{2}}$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$ $+$ $\frac{1}{1+x^{2}}$ $d(1+x^{2})$.
接下来,根据基本积分公式:
$\int$ $\frac{1}{x}$ $dx$ $=$ $\ln |x|$ $+$ $c$.
我们有:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $+$ $\frac{1}{1+x^{2}}d(1+x^{2})$ $=$ $x$ $+$ $\ln |1+x^{2}|$ $+$ $c$ $|_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $=$ $\frac{\pi}{2}$ $+$ $|\ln[1+(\frac{\pi}{2})^{2}]|$ $+$ $c$ $-$ $(-\frac{\pi}{2})$ $-$ $|\ln[1+(-\frac{\pi}{2})^{2}]|$ $-$ $c$ $=$ $\frac{\pi}{2}+\frac{\pi}{2}$ $=$ $\pi$.
又因为,$M$ 的积分上限 $\frac{\pi}{2}$ 减去 $M$ 的积分下限 $-\frac{\pi}{2}$ 也等于 $\pi$.
根据定积分的基本性质:
$\int_{a}^{b}$ $1$ $dx$ $=$ $b$ $-$ $a$.
我们知道:
$M$ $=$ $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $1$ $dx$.
补充:
如果是计算 $\int$ $\frac{2x}{1-x^{2}}$ $dx$, 则我们至少有以下两种计算方法:
$\int$ $\frac{2x}{1-x^{2}}$ $dx$ $=$ $-\int$ $\frac{1}{1-x^{2}}$ $=$ $-\ln |1-x^{2}|$ $+$ $c$;
或者:
$\int$ $\frac{2x}{1-x^{2}}$ $dx$ $=$ $\int$ $(\frac{1}{1-x}-\frac{1}{1+x})$ $dx$ $=$ $-\ln|x-1|$ $-$ $\ln|x+1|$ $+$ $c$ $=$ $-\ln|x^{2}-1|$ $+$ $c$.
至此,我们分别使用两种方法完成了对 $M$ 的化简计算。
根据定积分的比较定理:
设 $f(x)$ $\leqslant$ $g(x)$, $x$ $\in$ $[a,b]$, 则 $\int_{a}^{b}$ $f(x)$ $dx$ $\leqslant$ $\int_{a}^{b}$ $g(x)$ $dx$.
观察题目可知,题目中给出的三个定积分 $M$, $N$, $K$ 的上限和下限都是一样的,因此,我们可以使用上述比较定理比较他们的大小。
由于在 $M$, $N$, $K$ 中,我们目前已知的只有 $M$ 的数值,因此接下来我们先比较 $N$ 和 $K$ 中的积分函数与 $1$ 的大小关系。
首先来判断 $N$ 的积分函数和 $1$ 的大小关系。
当 $x$ $=$ $0$ 时,$1$ $+$ $x$ $=$ $e^{x}$ $=1$;
当 $x$ $<$ $0$ 时,$e^{x}$ 的减小速度小于 $1$ $+$ $x$ 的减小速度;
当 $x$ $>$ $0$ 时,$e^{x}$ 的增长速度大于 $1$ $+$ $x$ 的增长速度。
也就是说,在整个定义域内,$y$ $=$ $e^{x}$ 的函数图像始终在 $y$ $=$ $1$ $+$ $x$ 的上方或者和 $y$ $=$ $1$ $+$ $x$ 重合,他们二者的图像如图 2:
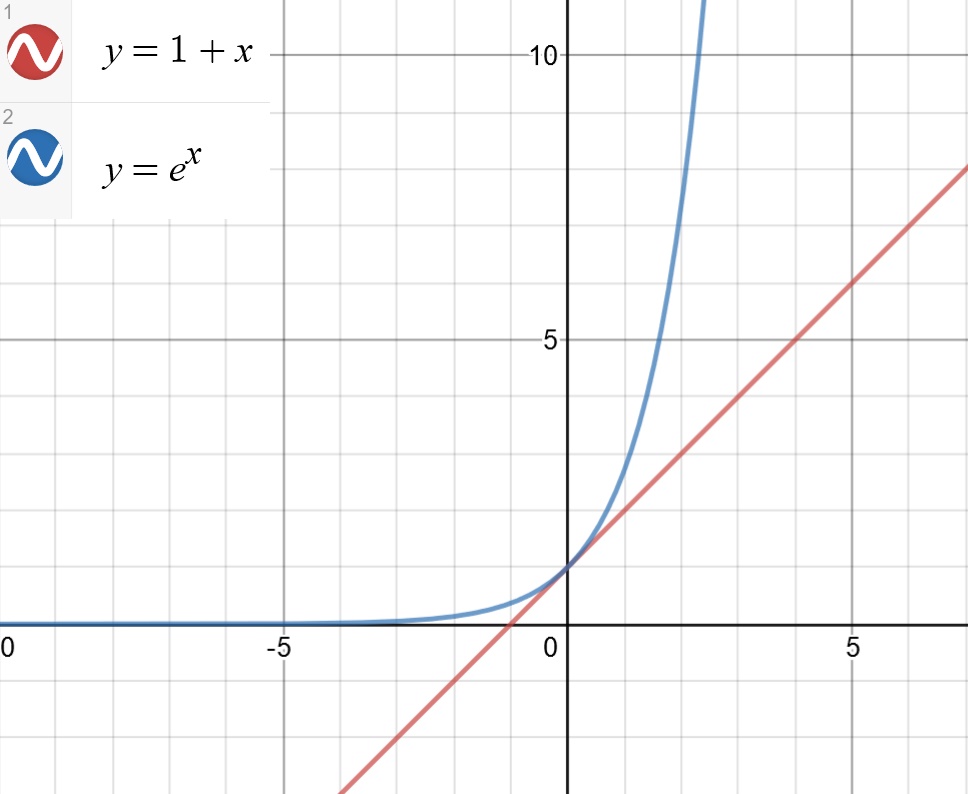
所以 $\frac{1+x}{e^{x}}$ $\leqslant$ $1$, $x$ $\in$ $[-\frac{\pi}{2}$, $\frac{\pi}{2}]$. 再来判断 $K$ 的积分函数和 $1$ 的大小关系。
我们知道,当 $x$ $\in$ $[$ $-\frac{\pi}{2},$ $\frac{\pi}{2}$ $]$ 上时,$y$ $=$ $\cos x$ $\geqslant$ $0$ 的,如图 3:
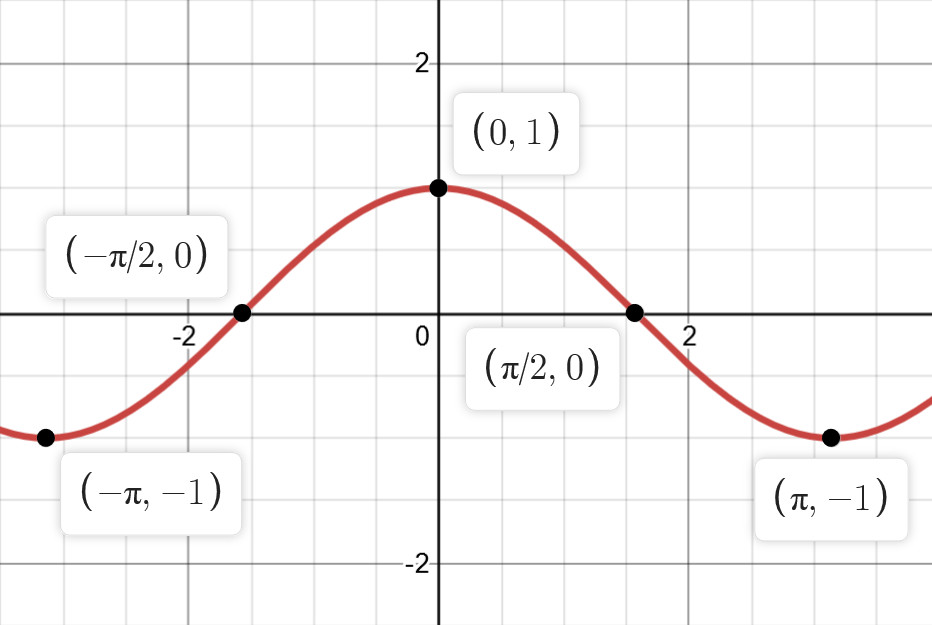
于是 $1$ $+$ $\sqrt{\cos x}$ $\geqslant$ $1$.
综上可知:
$K$ $\geqslant$ $M$ $\geqslant$ $N$, 正确选项是:C
EOF
2019 年 08 月 13 日,新版本的 XAMPP 发布,此次发布的安装程序包含以下组件:
本文消息来源:https://www.apachefriends.org/blog/new_xampp_20190813.html
XAMPP 官方下载地址:https://www.apachefriends.org/download.html