题目
编号:A2016220
设 $D$ 是由曲线 $y=\sqrt{1-x^{2}}$ $(0 \leqslant x \leqslant 1)$ 与 $\left\{\begin{matrix}
x= \cos ^{3} t;\\
y = \sin ^{3} t.
\end{matrix}\right.$ $(0 \leqslant t \leqslant \frac{\pi}{2})$ 围成的平面区域,求 $D$ 绕 $x$ 轴旋转一周所得旋转体的体积和表面积。
解析
由题可得:
$$
y=\sqrt{1-x^{2}} \Rightarrow
$$
$$
x^{2} + y^{2} = 1. ①
$$
$$
\left\{\begin{matrix}
x= \cos ^{3} t;\\
y = \sin ^{3} t.
\end{matrix}\right.
(0 \leqslant t \leqslant \frac{\pi}{2})
\Rightarrow
$$
$$
x^{\frac{2}{3}} + y^{\frac{2}{3}} = 1, (0 \leqslant x \leqslant 1). ②
$$
通过上面的变形计算得到的式子 $①$ 和 $②$ 可知,式子 $①$ 是一个圆心位于坐标系原点,半径长度为 $1$ 的圆形。而且,虽然我们不容易直接画出式子 $②$ 的图像,但从 $\frac{2}{3} < 2$ 也可以得知,在同一个坐标系中,式子 $②$ 的图象一定位于式子 $①$ 图象的内部。
题中所给的两条曲线在坐标系中的示意图如图 01 所示,其中绿色的区域即为平面区域 $D$:
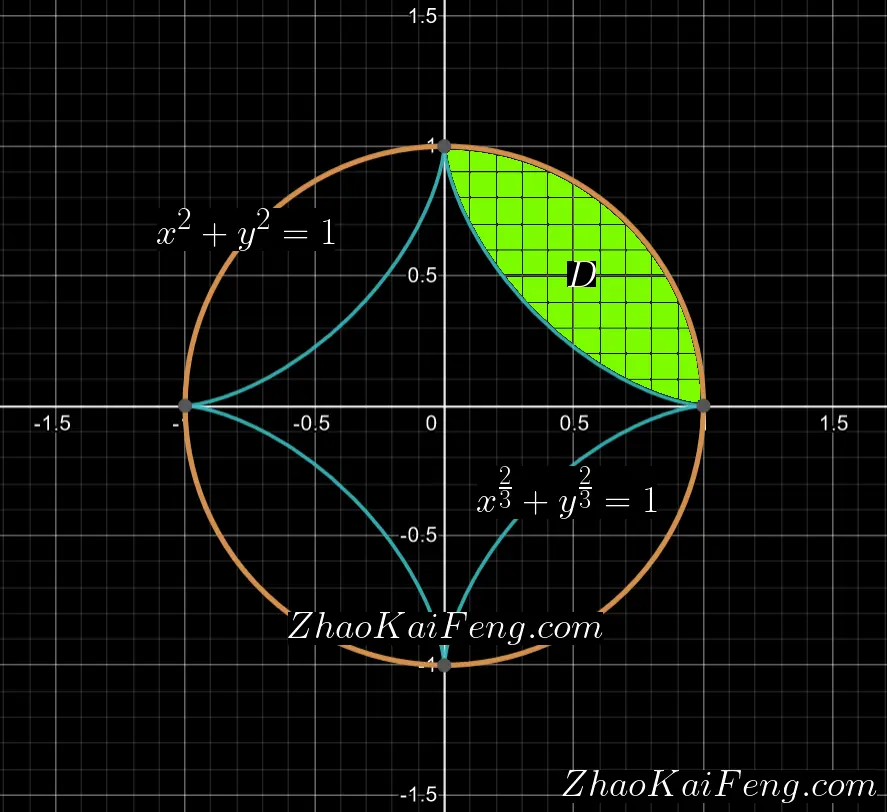
本题要求解的是平面区域 $D$ 绕 $x$ 轴旋转一周所得的旋转体的体积和表面积,其中:
图 01 中平面区域 $D$ 外侧的橙色曲线绕 $x$ 轴旋转一周所得的旋转体(半个球体)的三维示意图如图 02 所示:
绘制图 02 所用的 MATLAB 代码:
x = 0:0.01:1; [a,b,c]=cylinder(sqrt(1-x.*x),30); mesh(a,b,c)
图 01 中平面区域 $D$ 内侧的蓝色曲线绕 $x$ 轴旋转一周所得的旋转体的三维示意图如图 03 所示:
绘制图 03 所用的 MATLAB 代码:
x = 0:0.01:1; [a,b,c]=cylinder((1-x.^(2./3)).^(3./2),30); mesh(a,b,c)
经过前面的分析可知:
- 求平面区域 $D$ 绕 $x$ 轴旋转一周所得的旋转体的体积 $V$ 就是用图 01 中外侧橙色曲线绕 $x$ 旋转所得的旋转体的体积 $V_{1}$ 减去内测蓝色曲线绕 $x$ 旋转所得的旋转体的体积 $V_{2}$: $V = V_{1} – V_{2}$.
- 求平面区域 $D$ 绕 $x$ 轴旋转一周所得的旋转体的表面积 $S$ 就是图 01 中用外侧橙色曲线绕 $x$ 旋转所得的旋转体的表面积 $S_{1}$ 加上内测蓝色曲线绕 $x$ 旋转所得的旋转体的表面积 $S_{2}$: $S = S_{1} + S_{2}$.
一、求解旋转体的体积 $V$
$$
V = V_{1} – V_{2} \Rightarrow
$$
$$
V = \frac{1}{2} \cdot \frac{4}{3} \pi – \pi \int_{0}^{1} y^{2}(x) \mathrm{d}x ③ \Rightarrow
$$
注:
[1]. 球体的体积计算公式为:$v = \frac{4}{3} \pi r^{3}$, 其中 $r$ 为半径。
$$
V = \frac{2}{3} \pi – \pi \int_{\frac{\pi}{2}}^{0} (\sin ^{3} t)^{2} \mathrm{d} (\cos ^{3} t) ④ \Rightarrow
$$
注:
[1]. 当 $0 \leqslant t \leqslant \frac{\pi}{2}$ 时,$1 \leqslant \cos ^{3} t \leqslant 0$, 也就是说,若 $\cos ^{3} t \in (0, 1)$, 则 $t \in (\frac{\pi}{2}, 0)$. 由于积分上下限的取值范围是由积分变量决定的,因此,$③$ 式到 $④$ 式的变化过程中,所涉及积分的积分上下限的变换方式为:$\int_{0}^{1} \Rightarrow \int_{\frac{\pi}{2}}^{0}$.
$$
V = \frac{2}{3} \pi – \pi \int_{\frac{\pi}{2}}^{0} \sin ^{6} t \cdot (- 3 \cos ^{2} t \sin t) \mathrm{d} t \Rightarrow
$$
$$
V = \frac{2}{3} \pi – 3 \pi \int_{0}^{\frac{\pi}{2}} \sin ^{6} t \cdot (\cos ^{2} t \sin t) \mathrm{d} t \Rightarrow
$$
$$
V = \frac{2}{3} \pi – 3 \pi \int_{0}^{\frac{\pi}{2}} \sin ^{7} t \cdot (\cos ^{2} t) \mathrm{d} t \Rightarrow
$$
$$
V = \frac{2}{3} \pi – 3 \pi \int_{0}^{\frac{\pi}{2}} \sin ^{7} t \cdot (1 – \sin ^{2} t) \mathrm{d} t \Rightarrow
$$
$$
V = \frac{2}{3} \pi – 3 \pi \int_{0}^{\frac{\pi}{2}} (\sin ^{7} t – \sin ^{9} t) \mathrm{d} t \Rightarrow
$$
$$
华里士点火公式 \Rightarrow
$$
$$
V = \frac{2}{3} \pi – 3 \pi (\frac{6}{7} \cdot \frac{4}{5} \cdot \frac{2}{3} – \frac{8}{9} \cdot \frac{6}{7} \cdot \frac{4}{5} \cdot \frac{2}{3}) \Rightarrow
$$
$$
V = \frac{2}{3} \pi – 3 \pi (\frac{16}{35} – \frac{8}{9} \cdot \frac{16}{35}) \Rightarrow
$$
$$
V = \frac{2}{3} \pi – 3 \cdot \frac{16}{35} \pi (1 – \frac{8}{9}) \Rightarrow
$$
$$
V = \frac{2}{3} \pi – 3 \cdot \frac{16}{35} \cdot \frac{1}{9} \pi \Rightarrow
$$
$$
V = \frac{2}{3} \pi – \frac{16}{105} \pi = \frac{18}{35} \pi.
$$
二、求解旋转体的表面积 $S$
$$
S = S_{1} + S_{2} \Rightarrow
$$
$$
S = \frac{1}{2} \cdot 4 \pi + \int_{0}^{\frac{\pi}{2}} 2 \pi \sin^{3} t \cdot \sqrt{x^{‘2}(t) + y^{‘2}(t)} \mathrm{d} t \Rightarrow
$$
注:
[1]. 球体的表面积计算公式为:$s = 4 \pi r^{2}$, 其中 $r$ 为半径;
[2]. 表面积 $S_{2}$ 是由图 01 中区域 $D$ 外侧的橙色曲线绕 $x$ 轴旋转形成的旋转体的表面积,该橙色曲线的长度的微分为 $\sqrt{x^{‘2}(t) + y^{‘2}(t)} \mathrm{d} t$, 旋转所形成的旋转体某一位置的横截面周长为 $2 \pi r =$ $2 \pi \sin^{3} t \mathrm{d} t$, 其中,$r$ 表示横截面的半径。
$$
S = 2 \pi + 2 \pi \int_{0}^{\frac{\pi}{2}} \sin^{3} t \sqrt{x^{‘2}(t) + y^{‘2}(t)} \mathrm{d}t \Rightarrow
$$
$$
S = 2 \pi + 2 \pi \int_{0}^{\frac{\pi}{2}} \sin^{3} t \sqrt{(-3 \cos ^{2} t \sin t)^{2} + (3 \sin ^{2} t \cos t)^{2}} \mathrm{d}t \Rightarrow
$$
$$
S = 2 \pi + 2 \pi \int_{0}^{\frac{\pi}{2}} \sin^{3} t \sqrt{(9 \cos ^{4} t \sin ^{2} t) + (9 \sin ^{4} t \cos ^{2} t)} \mathrm{d}t \Rightarrow
$$
$$
S = 2 \pi + 2 \pi \int_{0}^{\frac{\pi}{2}} \sin^{3} t \sqrt{9 \cos ^{2} t \sin ^{2} t (\cos ^{2} t + \sin ^{2} t)} \mathrm{d}t \Rightarrow
$$
$$
S = 2 \pi + 2 \pi \int_{0}^{\frac{\pi}{2}} \sin^{3} t \cdot 3 \cos t \sin t \mathrm{d}t \Rightarrow
$$
$$
S = 2 \pi + 6 \pi \int_{0}^{\frac{\pi}{2}} \sin^{4} t \cdot \cos t\mathrm{d}t \Rightarrow
$$
$$
S = 2 \pi + 6 \pi \int_{0}^{1} \sin^{4} t \mathrm{d} (\sin t) \Rightarrow
$$
$$
S = 2 \pi + 6 \pi \int_{0}^{1} A^{4} t \mathrm{d} (A) \Rightarrow
$$
$$
S = 2 \pi + 6 \pi \cdot \frac{1}{5} A|_{0}^{1} \Rightarrow
$$
$$
S = 2 \pi + \frac{6}{5} \pi = \frac{16}{5} \pi.
$$