题目
计算二重积分 $\iint_{D} x(x+y) {\rm d} x {\rm d} y$, 其中 $D=$ $\left\{(x,y) | x^{2} + y^{2} \leqslant 2, y \geqslant x^{2} \right\}$.
解析
根据题目条件,我们可以绘制出如图 01 所示的示意图,其中绿色的部分就是积分区域 $D$.
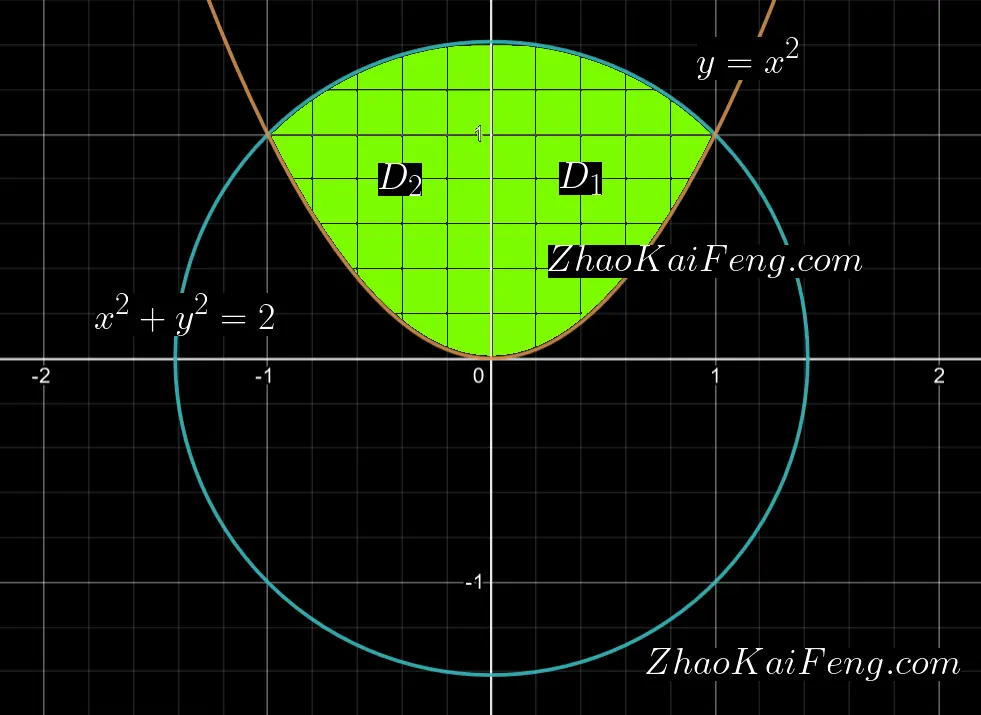
观察可知,积分区域 $D$ 是关于 $y$ 轴对称的,于是,以 $y$ 轴为界,我们可以将积分区域 $D$ 划分为如图 01 所示的 $D_{1}$ 和 $D_{2}$ 两个面积相等的区域。
又:
$$
\iint_{D} x(x+y) {\rm d} x {\rm d} y \Rightarrow
$$
$$
\iint_{D} x^{2} {\rm d} x {\rm d} y + \iint_{D} xy {\rm d} x {\rm d} y.
$$
由于积分区域 $D$ 是关于 $y$ 轴对称的,而函数 $f(x,y) = xy$ 是关于变量 $x$ 的奇函数,因此:
$$
\iint_{D} x^{2} {\rm d} x {\rm d} y + \iint_{D} xy {\rm d} x {\rm d} y =
$$
$$
\iint_{D} x^{2} {\rm d} x {\rm d} y + 0 =
$$
$$
\iint_{D} x^{2} {\rm d} x {\rm d} y = ①
$$
$$
2 \iint_{D_{1}} x^{2} {\rm d} x {\rm d} y. ②
$$
注:
[1]. 注意上面 $①$ 式和 $②$ 式积分区域的不同。
又:
$$
x^{2} + y^{2} = 2 \Rightarrow
$$
$$
y = \pm \sqrt{2-x^{2}}.
$$
若令:
$$
\sqrt{2-x^{2}} = x^{2}.
$$
注:
[1]. 由于积分区域 $D$ 全部位于 $y$ 轴的正半轴,因此,我们只需计算 $\sqrt{2-x^{2}} = x^{2}$, 而无需计算 $-\sqrt{2-x^{2}} = x^{2}$.
则:
$$
x = \pm 1.
$$
即曲线 $x^{2} + y^{2} = 2$ 与曲线 $y=x^{2}$ 相交点的横坐标分别是 $-1$ 和 $1$, 于是:
$$
2 \iint_{D_{1}} x^{2} {\rm d} x {\rm d} y =
$$
$$
2 \int_{0}^{1} x^{2} {\rm d} x {\rm d} y \int_{x^{2}}^{\sqrt{2-x^{2}}} 1 {\rm d}y =
$$
$$
2 \int_{0}^{1} x^{2}(\sqrt{2-x^{2}} – x^{2}) {\rm d} x =
$$
$$
2 [\int_{0}^{1} (x^{2} \sqrt{2-x^{2}}) {\rm d} x – \int_{0}^{1} x^{4} {\rm d} x].
$$
$$
2 \int_{0}^{1} (x^{2} \sqrt{2-x^{2}}) {\rm d} x – 2 \int_{0}^{1} x^{4} {\rm d} x =
$$
$$
2 \int_{0}^{1} (x^{2} \sqrt{2-x^{2}}){\rm d} x – 2 \frac{1}{5} x^{5} |_{0}^{1} =
$$
$$
2 \int_{0}^{1} (x^{2} \sqrt{2-x^{2}}){\rm d} x – \frac{2}{5}.
$$
接着,借助三角函数代换,令 $x = \sqrt{2} \sin A$, 于是:
$$
0 \leqslant x \leqslant 1 \Rightarrow
$$
$$
0 \leqslant \sqrt{2} \sin A \leqslant 1 \Rightarrow
$$
$$
0 \leqslant \sin A \leqslant \frac{\sqrt{2}}{2} \Rightarrow
$$
$$
0 \leqslant A \leqslant \frac{\pi}{4}.
$$
即:
$$
2 \int_{0}^{1} x^{2} \sqrt{2-x^{2}} – \frac{2}{5} \Rightarrow
$$
$$
2 \int_{0}^{\frac{\pi}{4}} 2 \sin^{2}A \cdot \sqrt{2} \cos A {\rm d}(\sqrt{2} \sin A) – \frac{2}{5} =
$$
$$
2 \int_{0}^{\frac{\pi}{4}} 2 \sin^{2}A \cdot 2 \cos^{2} A {\rm d}(A) – \frac{2}{5} =
$$
$$
8 \int_{0}^{\frac{\pi}{4}} \sin^{2}A \cdot \cos^{2} A {\rm d}(A) – \frac{2}{5} =
$$
$$
8 \int_{0}^{\frac{\pi}{4}} (\sin A \cos A) \cdot (\sin A \cos A) {\rm d}(A) – \frac{2}{5} = ③
$$
$$
8 \cdot \frac{1}{4} \int_{0}^{\frac{\pi}{4}} \sin^{2} (2A) {\rm d}(A) – \frac{2}{5} = ④
$$
注:
[1]. $③$ 式到 $④$ 式的变换过程利用了如下公式:
$\sin 2 \alpha = 2 \sin \alpha \cos \alpha.$
$$
2 \cdot \frac{1}{2} \int_{0}^{\frac{\pi}{4}} \sin^{2}(2A) {\rm d}(2A) – \frac{2}{5} =
$$
注:
[1]. 若令 $B = 2A$, 则由 $0 \leqslant A \leqslant \frac{\pi}{4}$ 可知:$0 \leqslant B \leqslant \frac{\pi}{2}.$
$$
\int_{0}^{\frac{\pi}{2}} \sin^{2} B {\rm d}(B) – \frac{2}{5} = ⑤
$$
$$
\frac{1}{2} \cdot \frac{\pi}{2} – \frac{2}{5} = ⑥
$$
注:
[1]. $⑤$ 式到 $⑥$ 式的变换过程利用了华里士“点火公式”。
$$
\frac{\pi}{4} – \frac{2}{5}.
$$