题目
设平面区域 $D$ 由直线 $x=3y$, $y=3x$ 与 $x+y=8$ 围成。计算 $\iint_{D} x^{2} dxdy.$
解析
本题就是一般情况下二重积分的计算问题。计算二重积分,首先就要画出积分区域 $D$, 为了方便接下来的绘图,我们可以对题目给出的三个直线的函数做一下变换:
$$
\left\{\begin{matrix}
x=3y;\\
y=3x;\\
x+y=8.
\end{matrix}\right.
\Rightarrow
$$
$$
\left\{\begin{matrix}
y=\frac{1}{3}x;\\
y=3x;\\
y=-x+8.
\end{matrix}\right. ①
$$
通过对 $①$ 中的三个函数式两两联立,可以求得它们之间交叉点的坐标,并据此画出区域 $D$ 的示意图,如图 01 所示:
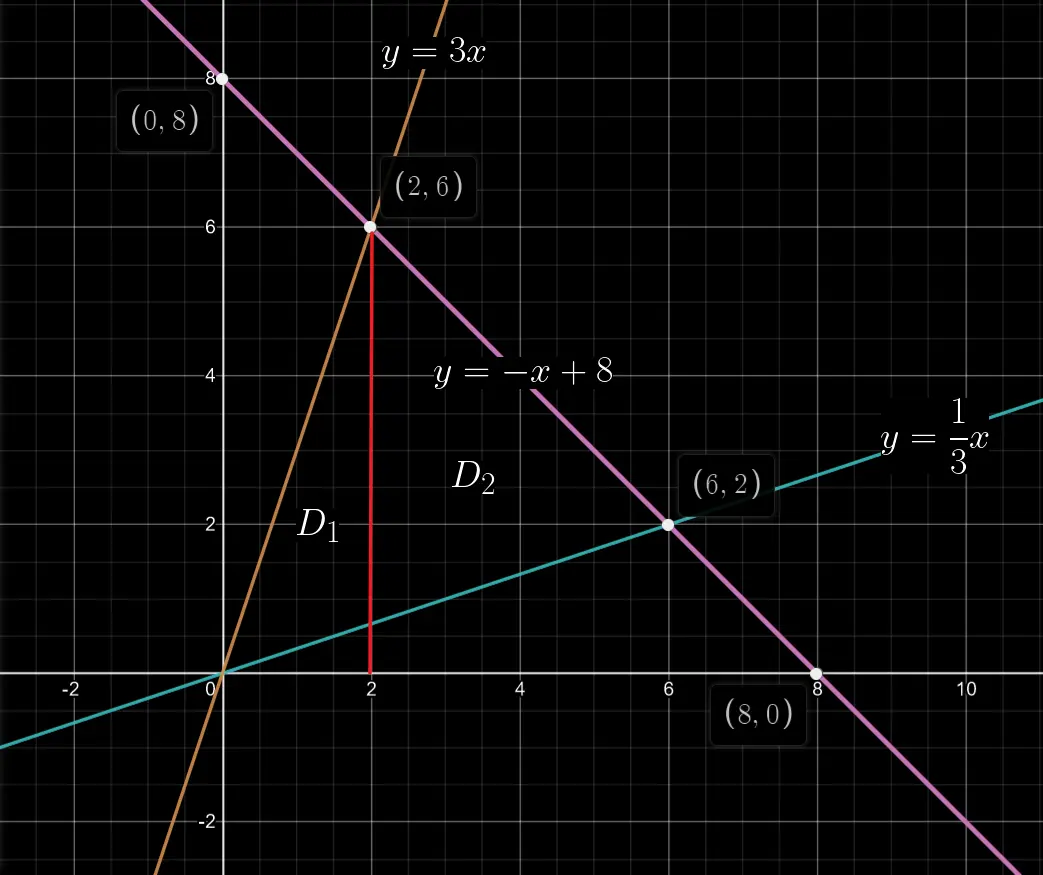
观察图 01 可知,我们可以令 $x=2$ 这条线(红色线)作为分界线,将区域 $D$ 划分成 $D_{1}$ 和 $D_{2}$ 两个区域,分别积分,之后再求和即可。
于是:
$$
D_{1} = \int_{0}^{2} x^{2} dx \int_{\frac{x}{3}}^{3x} dy \Rightarrow
$$
$$
\int_{0}^{2} x^{2}(3x-\frac{x}{3}) dx \Rightarrow
$$
$$
\frac{8}{3} \int_{0}^{2} x^{3} dx \Rightarrow
$$
$$
\frac{8}{3} \cdot \frac{1}{4} x^{4} |_{0}^{2} \Rightarrow
$$
$$
\frac{2}{3} \cdot 16 = \frac{32}{3}.
$$
$$
D_{2} = \int_{2}^{6} x^{2} dx \int_{\frac{x}{3}}^{8-x} dy \Rightarrow
$$
$$
\int_{2}^{6} x^{2}(8-x-\frac{x}{3}) dx \Rightarrow
$$
$$
8 \int_{2}^{6} x^{2} dx – \frac{4}{3} \int_{2}^{6} x^{3} dx \Rightarrow
$$
$$
8 \cdot \frac{1}{3} x^{3} |_{2}^{6} – \frac{4}{3} \cdot \frac{1}{4} x^{4}|_{2}^{6} \Rightarrow
$$
$$
\frac{8}{3}(216-8) – \frac{1}{3}(1296-16) = 128.
$$
于是:
$$
\iint_{D} x^{2} dxdy =
$$
$$
\iint_{D_{1}} x^{2} dxdy + \iint_{D_{2}} x^{2} dxdy =
$$
$$
\frac{32}{3} + 128 = \frac{416}{3}.
$$