初等变换求逆法的形象理解：把单位矩阵 E 看作一张“白纸”或“原点”

前言

本文将通过几个例子来解释如何通过把单位矩阵 $E$ 看作一张“白纸”或“原点”的方式来形象化地理解一些做题思路——这种理解并不是严格的数学推导，但是能帮助我们化解一些题目“为什么要这么做”的疑问。

例一

设 $A=\left|\begin{array}{ccc}1& 1& 0\\ 1& 0& 2\\ 3& 2& 2\end{array}\right|$ 经过有限次的初等变换转化成为 $B=\left|\begin{array}{ccc}1& 0& 2\\ 1& 2& -2\\ 2& 3& -2\end{array}\right|$, 求一个可逆矩阵 $P$, 使 $PA=B$.

由于 $A$ 是左乘 $P$, 根据“左行右列”的原则，$PA=B$ 的含义就是：

对 $A$ 做一系列的行变换，使得 $A$ 变成 $B$.

但是，对于如何求出 $P$, 线性代数的课本中几乎没有明确的公式或者性质可用。

但是，我们知道，当我们做一些【行变换操作】将 $A$ 变成 $B$ 的过程中，这些【行变换操作】我们是可以做出来的，而这些【行变换操作】其实就对应着矩阵 $P$. 进而可以想到，如果我们能够将这些【行变换操作】组合起来，形成对应的矩阵，那么，这个矩阵就是矩阵 $P$.

为了达成上面的目标，我们就需要一个【平台】，这个平台必须足够【基础】，能反映并记录施加在其上每一步变化（相当于一张“白纸”）。这个【平台】最佳的选择就是——单位矩阵 $E$.

如果我们把对 $A$ 在变成 $B$ 的过程中进行的每一步【行】初等变换都同步施加到初始状态为单位矩阵的矩阵上，那么，在 $A$ 变成 $B$ 的时候，我们就得到了一个满足 $PA=B$ 条件的可逆矩阵 $P$, 形式如下：

$$(A,E)\to \mathrm{初}\mathrm{等}\mathrm{行}\mathrm{变}\mathrm{换}\to (B,P)\Rightarrow$$

$$PA=B.$$

同样的，如果要找的是满足 $AP=B$ 的可逆矩阵 $P$, 则要对 $A$ 做初等列变换，形式如下：

$$(\genfrac{}{}{0ex}{}{A}{E})\to \mathrm{初}\mathrm{等}\mathrm{列}\mathrm{变}\mathrm{换}\to (\genfrac{}{}{0ex}{}{B}{P})\Rightarrow$$

注意：若要使用列变换，则 $E$ 相对于 $A$ 的位置应该是【竖着】放置的，因为列变换影响的是列，只有竖着放才能让 $E$ 记录到所做的列变换，【横着】放置的 $E$ 只能记录到所作的行变换。

$$AP=B.$$

对于本题，有：

$$\left|\begin{array}{ccccccc}1& 1& 0& |& 1& 0& 0\\ 1& 0& 2& |& 0& 1& 0\\ 3& 2& 2& |& 0& 0& 1\end{array}\right|\Rightarrow$$

$$\left|\begin{array}{ccccccc}1& 0& 2& |& 0& 1& 0\\ 1& 2& -2& |& 2& -1& 0\\ 2& 3& -2& |& 1& -2& 1\end{array}\right|.$$

于是：

$$P=\left|\begin{array}{ccc}0& 1& 0\\ 2& -1& 0\\ 1& -2& 1\end{array}\right|.$$

由于初等行变换的方式不止上述一种，因此，也可以有：

$$P=\left|\begin{array}{ccc}0& 1& 0\\ 0& -2& 1\\ 1& -2& 1\end{array}\right|.$$

例二

求矩阵 $A=\left|\begin{array}{ccc}1& 2& 3\\ 2& -5& 3\\ 3& 7& 4\end{array}\right|$ 的逆矩阵。

求逆矩阵的方法有多种，对于这种以实数方式完全给定的矩阵求其逆矩阵，一般使用如下公式：

$$(A,E)\to \mathrm{初}\mathrm{等}\mathrm{行}\mathrm{变}\mathrm{换}\to (E,A^{-1}).$$

或者：

$$(\genfrac{}{}{0ex}{}{A}{E})\to \mathrm{初}\mathrm{等}\mathrm{列}\mathrm{变}\mathrm{换}\to (\genfrac{}{}{0ex}{}{E}{A^{-1}}).$$

那么，如何理解上面这两个公式呢？

如果我们把 $E$ 看作“数轴”的“原点”，那么，$A$ 和 $A^{-1}$ 就是对称于“原点” $E$ 分布在“数轴”上的。在这个“数轴”上，移动一个矩阵的方式就是对其做初等变换（横轴做初等行变换，纵轴做初等列变换），【不同】的初等行（列）变换会导致矩阵（无论是不是同一个矩阵）在“数轴”上移动【不同】的“距离”，而【相同】的初等行（列）变换会导致矩阵（无论是不是同一个矩阵）在“数轴”上移动【相同】的距离。

于是，如果，我们同时对 $A$ 和 $E$ 施加同样的初等变换，那么，就相当于把 $A$ 和 $E$ 做了平移，当 $A$ 变成（移动到）$E$ 的时候，$E$ 就变成（移动到）了 $A^{-1}$, 如图 1 ~ 2 所示：

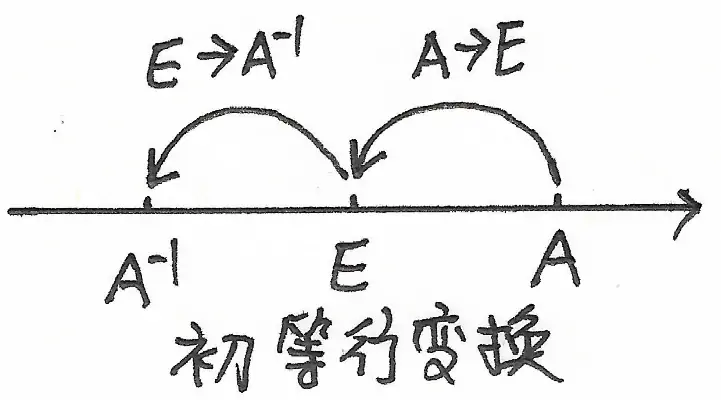
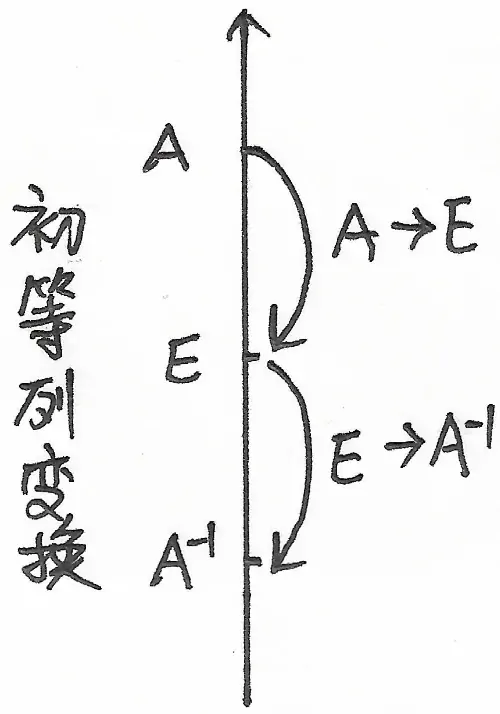
于是，有：

$$(A,E)=$$

$$\left|\begin{array}{ccccccc}1& 2& 3& |& 1& 0& 0\\ 2& -5& 3& |& 0& 1& 0\\ 3& 7& 4& |& 0& 0& 1\end{array}\right|\Rightarrow$$

$$\left|\begin{array}{ccccccc}1& 0& 0& |& -\frac{41}{48}& \frac{13}{48}& \frac{7}{16}\\ 0& 1& 0& |& \frac{1}{48}& -\frac{5}{48}& \frac{1}{16}\\ 0& 0& 1& |& \frac{29}{48}& -\frac{1}{48}& -\frac{3}{16}\end{array}\right|.$$

于是：

$$A^{-1}=\left|\begin{array}{ccc}-\frac{41}{48}& \frac{13}{48}& \frac{7}{16}\\ \frac{1}{48}& -\frac{5}{48}& \frac{1}{16}\\ \frac{29}{48}& -\frac{1}{48}& -\frac{3}{16}\end{array}\right|.$$

根据上面的理解方式，我们也可以理解为什么当一个行列式的值为 $0$ 的时候，这个行列式就是不可逆的了：因为 $|E|\ne 0$, 所以，当一个行列式等于零的时候，它永远都无法通过行变换或者列变换变成 $E$.

EOF