题目
行列式 $\begin{vmatrix}
0 & a & b & 0\\
a & 0 & 0 & b\\
0 & c & d & 0\\
c & 0 & 0 & d
\end{vmatrix} = ?$
$$
A. (ad-bc)^{2}
$$
$$
B. -(ad-bc)^{2}
$$
$$
C. a^{2}d^{2} – b^{2}c^{2}
$$
$$
D. b^{2}c^{2} – a^{2}d^{2}.
$$
解析
该行列式中的 $0$ 分布得很规范,因此考虑使用分块矩阵展开式(拉普拉斯展开式)计算。但是在使用分块矩阵展开式的时候,要特别注意,必须是方形的“分块”才可以展开相乘。因此,下面这种做法就是错误的,如图 1 所示:
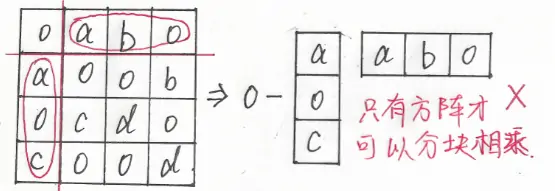
图 1
在使用分块矩阵展开式之前,最重要的就是变形出适合分块展开的形式。有时候,当数字 $0$ 和字母混合在一起的时候,不容易看出来该如何变形,这时候,可以单独把其中的 $0$ 摘出来,寻找变形的方法,如图 2 所示:
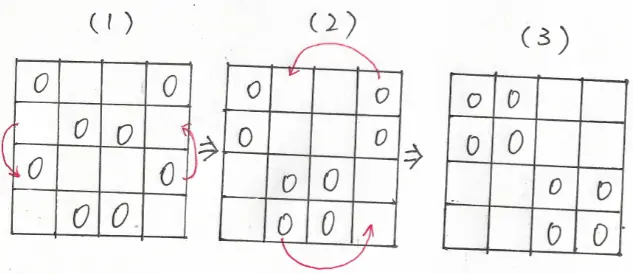
图 2
本题的解题过程如下:
$$
\begin{vmatrix}
0 & a & b & 0\\
a & 0 & 0 & b\\
0 & c & d & 0\\
c & 0 & 0 & d
\end{vmatrix} \Rightarrow
$$
$$
(-1)
\begin{vmatrix}
0 & a & b & 0\\
0 & c & d & 0\\
a & 0 & 0 & b\\
c & 0 & 0 & d
\end{vmatrix} \Rightarrow
$$
$$
(-1)(-1)
\begin{vmatrix}
0 & 0 & b & a\\
0 & 0 & d & c\\
a & b & 0 & 0\\
c & d & 0 & 0
\end{vmatrix} \Rightarrow
$$
$$
-(1)
\begin{vmatrix}
a & b\\
c & d
\end{vmatrix}
\begin{vmatrix}
b & a\\
d & c
\end{vmatrix}
$$
$$
-(1)[(ad-bc)(bc-ad)] =
$$
$$
-(ad-bc)^{2}.
$$
综上可知,正确选项为 $B$.
EOF