这个旋转体是个“甜甜圈”！你会求这个甜甜圈的体积吗？

一、题目

难度评级：

一、前言

首先，区域 $D$ 其实就是一个圆形面，如图 01 所示：

如果将这个圆形绘制在三维空间中，看上去就是如图 02 所示的红色圆圈：

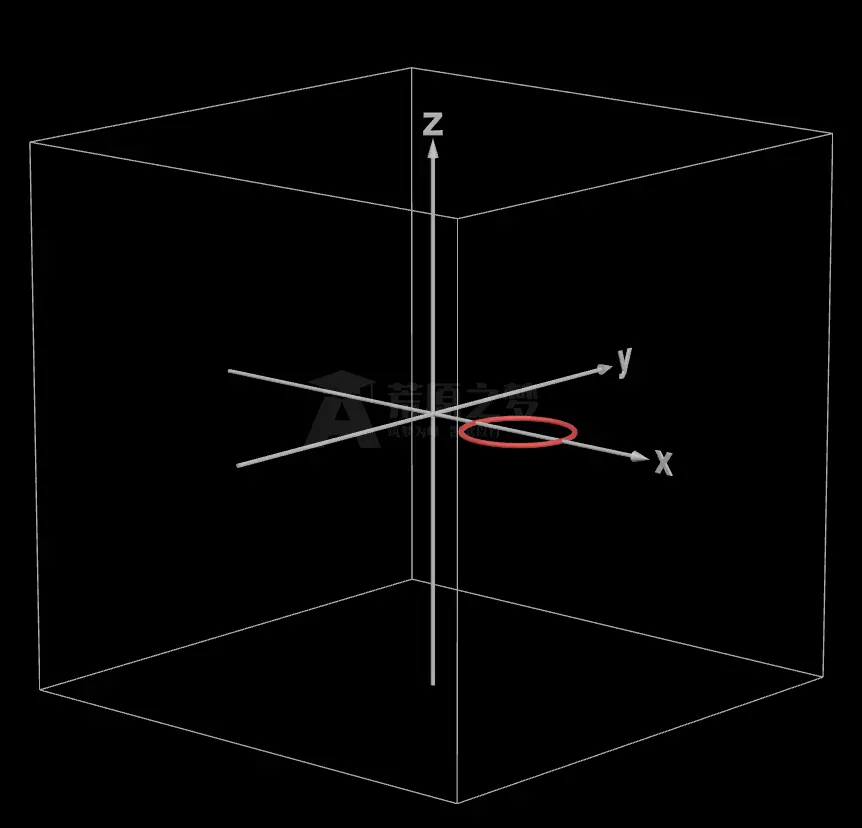
如果让这个区域 $D$ 绕 $Y$ 轴旋转一周，那么，就会形成如图 03 所示的绿色甜甜圈（不知道这个“绿色甜甜圈”好不好吃啊^v^）：

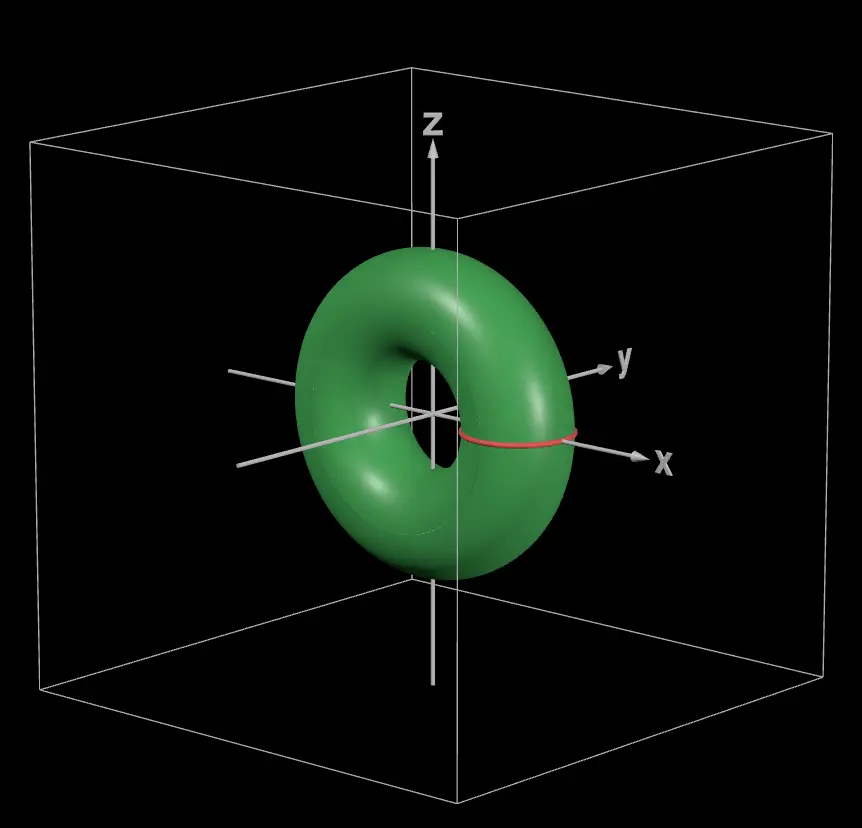
Note

荒原之梦考研数学坚持“讲究”不“将就”，同学们检查一下可以发现，上面的图 02 和图 03 无论在图片的尺寸，还是坐标轴的相对位置上，都是一个像素都不差的，完全一致。

zhaokaifeng.com

由 $( x – 2 ) ^ { 2 } + y ^ { 2 }$ $=$ $1$, 我们可得：

$$
\begin{cases}
& y = \sqrt{1- (x-2)^{2}} \\ \\
& y = – \sqrt{1 – (x-2)^{2}}
\end{cases}
$$

其中，$y$ $=$ $\sqrt{1- (x-2)^{2}}$ 绕 $Y$ 轴旋转一圈之后，得到的其实是“甜甜圈”位于 $Y$ 轴正半轴所在空间中的面积，也就是这个“甜甜圈”的一半，因此，如果我们用 $y$ $=$ $\textcolor{springgreen}{\sqrt{1- (x-2)^{2}}}$ 作为被积函数，那么，就需要乘以 $\textcolor{orangered}{2}$ 才能得到“甜甜圈”真正的体积。

Important

旋转体体积的计算几乎是每年考研的必考知识点，同学们一定要熟练掌握这部分内容的计算公式和常见题型。

zhaokaifeng.com

好啦，接下来就是利用绕 $Y$ 轴旋转的旋转体体积求解公式进行计算了：

$$
\begin{aligned}
V \\ \\
& = \textcolor{orangered}{2} \cdot 2 \pi \cdot \int _ { 1 } ^ { 3 } x \cdot \textcolor{springgreen}{\sqrt { 1 – ( x – 2 ) ^ { 2 } } \mathrm { ~ d } x} \\
& \underrightarrow{x – 2 = t \ } \quad 4 \pi \int _ { – 1 } ^ { 1 } ( t + 2 ) \sqrt { 1 – t ^ { 2 } } \mathrm { ~ d } t \\ \\
& = \textcolor{blue}{4 \pi \int _ { – 1 } ^ { 1 } t \sqrt { 1 – t ^ { 2 } } \mathrm { ~ d } t} + 8 \pi \int _ { – 1 } ^ { 1 } \sqrt { 1 – t ^ { 2 } } \mathrm { ~ d } t \\ \\
& = \textcolor{blue}{0} + 1 6 \pi \int _ { 0 } ^ { 1 } \sqrt { 1 – t ^ { 2 } } \mathrm { ~ d } t \\ \\
& = 1 6 \pi \times \frac { 1 } { 4 } \pi \times 1 ^ { 2 } = 4 \pi ^ { 2 }
\end{aligned}
$$

综上可知，$D$ 绕 $Y$ 轴旋转一周所得旋转体的体积是：$4 \pi ^ { 2 }$