绘制完成的示意图一定要用阴影线重点标注出来

一、题目

已知，有曲线 $y=\sqrt{x-1}$, 过原点作其切线, 则以曲线、切线及 $x$ 轴所围成平面图形绕 $x$轴旋转一圈所得到的表面积是多少？

难度评级：

二、解析

解答这类问题的关键是要绘制出示意图并仔细分析要求解的内容涉及哪些曲线？在什么区间上？需要拼接计算还是用一部分减去另一部分的方法计算？

根据题目，我们可以绘制出如下示意图：

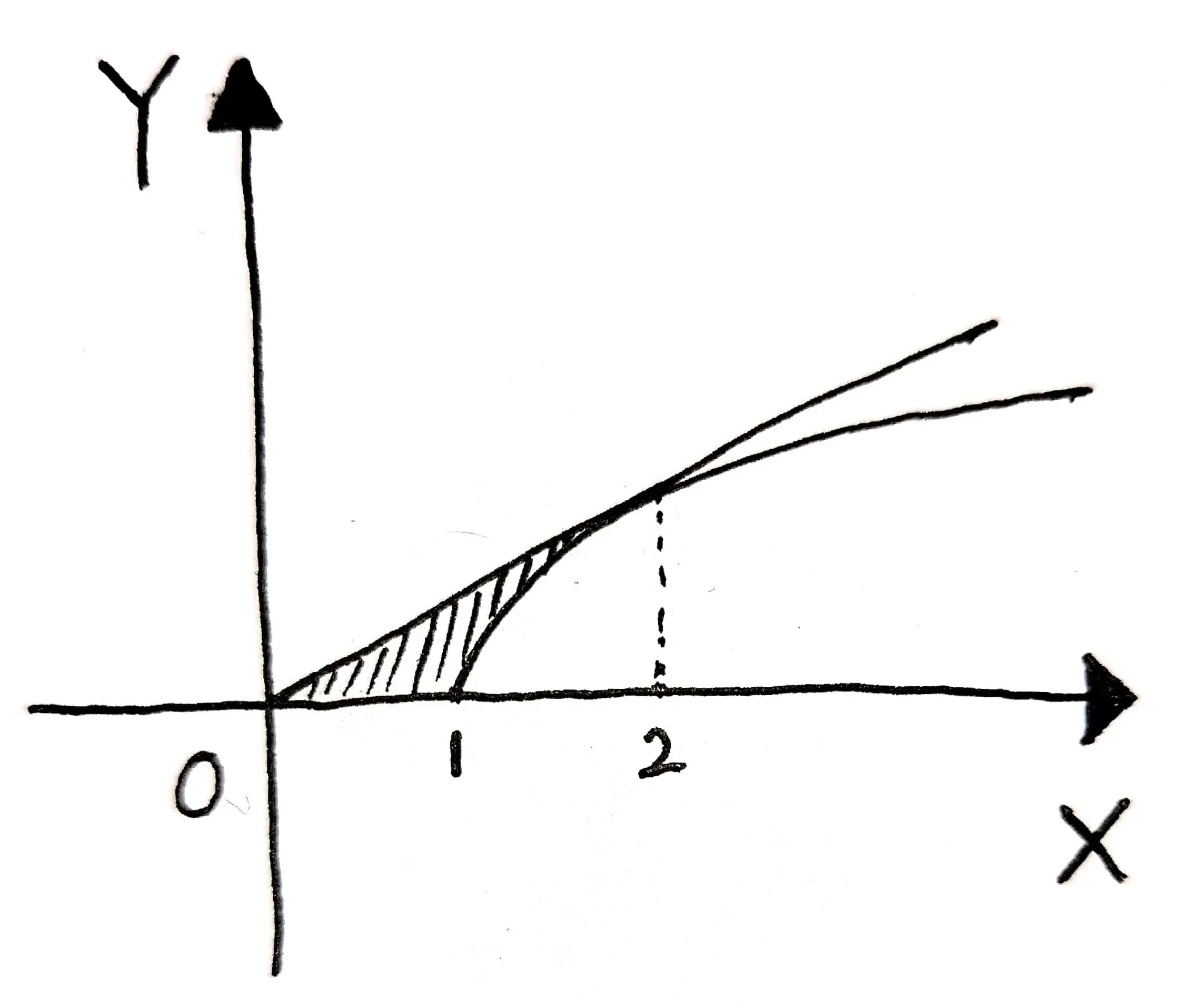
首先求解切线方程：

$$
y=(x-1)^{\frac{1}{2}} \Rightarrow y^{\prime}=\frac{1}{2}(x-1)^{\frac{-1}{2}}=\frac{1}{2 \sqrt{x-1}}
$$

$$
P\left(x_{0}, y_{0}\right) \Rightarrow k=\frac{1}{2 \sqrt{x_{0}-1}} \Rightarrow
$$

$$
y-y_{0}=k\left(x-x_{0}\right) \Rightarrow
$$

$$
y-\sqrt{x_{0}-1}=\frac{1}{2 \sqrt{x_{0}-1}}\left(x-x_{0}\right) \Rightarrow x=0, y=0 \Rightarrow
$$

$$
-\sqrt{x_{0}-1}=\frac{1}{2 \sqrt{x_{0}-1}} \Rightarrow x_{0}-1=\frac{1}{2} x_{0} \Rightarrow
$$

$$
\frac{1}{2} x_{0}=1 \Rightarrow x_{0}=2, \quad y-1=\frac{1}{2}(x-2) \Rightarrow
$$

于是可得，切线方程为：

$$
y=\frac{1}{2} x
$$

求解切线 $y = \frac{1}{2} x$ 旋转产生的旋转体的侧面积 $S_{1}$:

$$
S_{1}=2 \pi \int_{\textcolor{orangered}{ 0 }}^{\textcolor{orangered}{ 2 }}\left|\frac{1}{2} x\right| \cdot \sqrt{1+\left(\frac{1}{2} x\right)^{\prime 2}} \mathrm{~ d} x \Rightarrow
$$

$$
S_{1}=\pi \int_{0}^{2} x \cdot \sqrt{1+\frac{1}{4}} \mathrm{~ d} x \Rightarrow
$$

$$
S_{1}=\left.\frac{\pi \sqrt{5}}{2} \cdot \frac{1}{2} x^{2}\right|_{0} ^{2}=\pi \sqrt{5}
$$

求解曲线 $y = \sqrt{x – 1}$ 旋转产生的旋转体的侧面积 $S_{2}$:

$$
S_{2}=2 \pi \int_{\textcolor{springgreen}{ 1 }}^{\textcolor{springgreen}{ 2 }}|\sqrt{x-1}| \sqrt{1+\left(\frac{1}{2 \sqrt{x-1}}\right)^{2}} \mathrm{~ d} x \Rightarrow
$$

$$
S_{2}=2 \pi \int_{1}^{2} \sqrt{x-1} \cdot \frac{\sqrt{4 x-3}}{2 \sqrt{x-1}} \mathrm{~ d} x \Rightarrow
$$

$$
S_{2}=\pi \int_{0}^{2} \sqrt{4 x-3} \mathrm{~ d} x \cdot 7 \Rightarrow
$$

$$
S_{2}=\left.\frac{\pi}{6}(4 x-3)^{\frac{3}{2}}\right|_{1} ^{2} \Rightarrow
$$

$$
S_{2}=\frac{\pi}{6}\left(5^{\frac{3}{2}}-1\right)
$$

综上可知，总面积为：

$$
S=S_{1}+S_{2}=\pi\left(\frac{11}{6} \sqrt{5}-\frac{1}{6}\right) \Rightarrow
$$

$$
S=\frac{\pi}{6}(11 \sqrt{5}-1)
$$

---