2015年考研数二第06题解析

题目

设 $D$ 是第一象限中由曲线 $2xy=1$, $4xy=1$ 与直线 $y=x$, $y=\sqrt{3}x$ 围成的平面区域，函数 $f(x,y)$ 在 $D$ 上连续，则 ${\iint }_{D}f(x,y)dxdy=?$

$$A.{\int }_{\frac{\pi }{2}}^{\frac{\pi }{3}}d\theta {\int }_{\frac{1}{2\sin 2\theta }}^{\frac{1}{\sin 2\theta }}f(r\cos \theta ,r\sin \theta )rdr$$

$$B.{\int }_{\frac{\pi }{2}}^{\frac{\pi }{3}}d\theta {\int }_{\frac{1}{\sqrt{2\sin 2\theta }}}^{\frac{1}{\sqrt{\sin 2\theta }}}f(r\cos \theta ,r\sin \theta )rdr$$

$$C.{\int }_{\frac{\pi }{2}}^{\frac{\pi }{3}}d\theta {\int }_{\frac{1}{2\sin 2\theta }}^{\frac{1}{\sin 2\theta }}f(r\cos \theta ,r\sin \theta )dr$$

$$D.{\int }_{\frac{\pi }{2}}^{\frac{\pi }{3}}d\theta {\int }_{\frac{1}{\sqrt{2\sin 2\theta }}}^{\frac{1}{\sqrt{\sin 2\theta }}}f(r\cos \theta ,r\sin \theta )dr$$

解析

本题是考察使用极坐标变换将二重积分变成累次积分的知识。

首先，在极坐标系中使用累次积分时，右侧对 $r$ 积分时是需要写成 $\int frdx$ 的，不能少了式子中的 $r$, 因此，可以排除 $C$, $D$ 两项。

如图 1, 对 $\theta$ 积分时，积分下限 ${\theta }_1=\frac{\pi }{4}$, 积分上限 ${\theta }_2=\frac{\pi }{3}$, 这两个数值可以通过画图和使用三角函数计算出来。

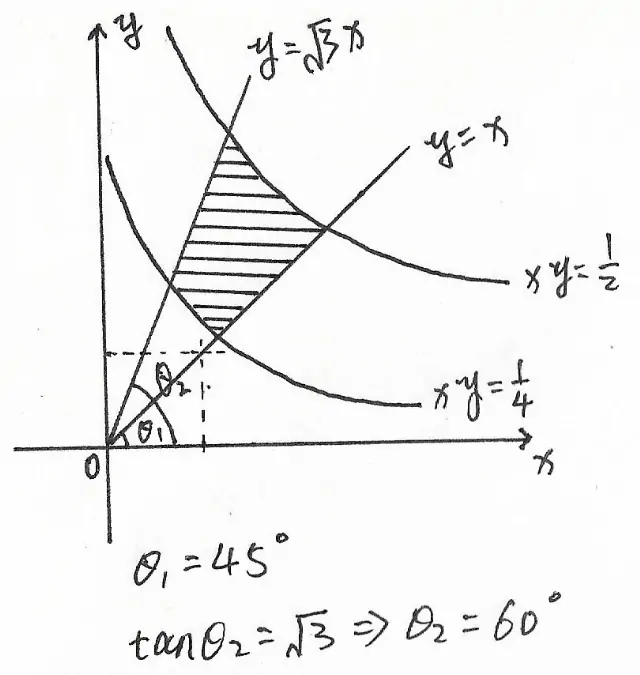
接着，设 $x=r\cos \theta$, $y=r\sin \theta$, 于是：

$$xy=\frac{1}{4}\Rightarrow$$

$$r^2\sin \theta \cos \theta =\frac{1}{4}\Rightarrow$$

$$r^2\frac{1}{2}\sin 2\theta =\frac{1}{4}\Rightarrow$$

$$r^2\sin 2\theta =\frac{1}{2}\Rightarrow$$

$$r=\frac{1}{\sqrt{2\sin 2\theta }}.$$

$$xy=\frac{1}{2}\Rightarrow$$

$$r^2\sin \theta \cos \theta =\frac{1}{2}\Rightarrow$$

$$r^2\frac{1}{2}\sin 2\theta =\frac{1}{2}\Rightarrow$$

$$r=\frac{1}{\sqrt{\sin 2\theta }}.$$

于是可知，对 $\theta$ 进行积分时，积分下限是 $\frac{1}{\sqrt{2\sin 2\theta }}$, 积分上限是 $\frac{1}{\sqrt{\sin 2\theta }}$.

综上可知，正确选项为 $B$.

EOF